4.2 + 4.3

Common logarithm

Base 10

Log x = log_10^x

Natural Base

Irrational number e. Written using ln x

Log_ex = ln x

Log_b(1) = 0

b^0 = 1

log_b(b) = 1

b^1=b

log_b(b)^x=x

b^x = b^x

If log_b(x) = log_b(y) then

x = y because log is one to one

Change of base property

Inverse properties

Logs and exponential with the same base undo each other

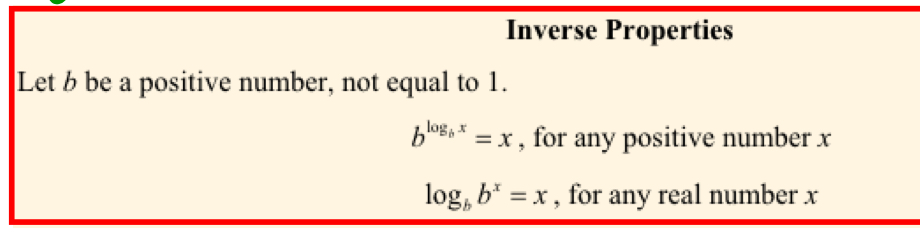
Natural log and parentheses

Anytime there’s no parentheses you can assume that ln only applies to what’s directly after it

Exponent properties of logarithms

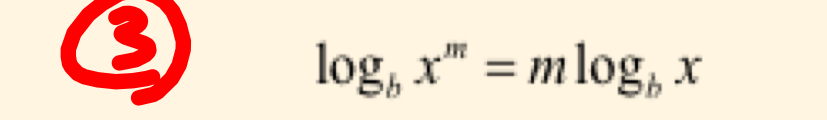
Sum properties of logarithms

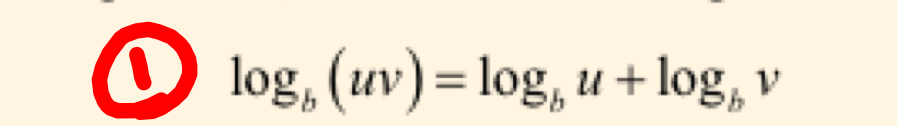
Difference properties of logarithms

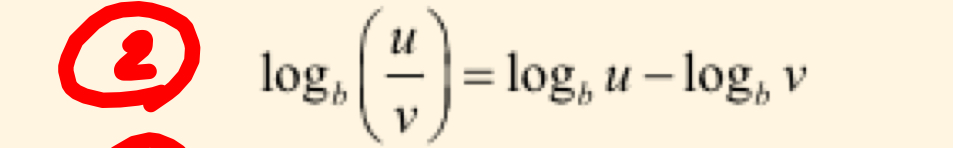
A square root can be rewritten as

One half power

Logarithms Strategy

1. Isolate all log terms onto one side of the equation

2. Use log properties to write it as an equation with only one log term

3. Use the definition of log to rewrite in equivalent exponent form

4. Finish solving

5. Check answer to see if it fits. No logs of negative numbers or zeros

Strategy for solving exponential equations when the bases match

If you can get an exponential equation in the form of b^n = b^m then you may use the one to one property and n = m

Strategy for solving exponential equations generally

Move the items around to isolate the exponential on one side of the equation. Rewrite as an equivalent log equation, or take log of both sides of the equation

Strategy for solving exponential equations with exponent term on both sides

If there is an exponential term on both sides of the equation, you need to take the log of both sides