E100 Topic 2 - Political Economy

What are the 4 democratic principles that a group decision function must satisfy

• Decisiveness: Unique choice for any set of individual preferences - would be violated by a minority rule but is satisfied by majority rule

• Anonymity: All individuals are treated the same. Any permutation of pairs of ballots leaves the GDF unchanged. Violated by dictatorship.

• Neutrality: all alternatives are treated the same: if the support for two alternatives is the same, i.e. the same group of people want to legalise weed as want assisted dying, then the GDF selection should be the same

• Positive responsiveness: If D = 1 or 0 and one individual changes ballot from -1 to 0 or 1, and all other ballots stay the same, then D = 1. Embeds monotonicity (that if some votes change in 1 direction and all else is unchanged, the GDF should not change in the opposite direction) and one-vote responsiveness (one vote should be enough to break an indifferent decision).

May’s theorem

The only voting rule that satisfies the 4 democratic principles is the simple majority rule (SMR), proved via the Tie Lemma

Tie Lemma and it’s uses

Use in the proof of May’s Theorem

Assumptions of the Condorcet Jury Theorem

• Jury of citizens decide ‘guilty’ (G) or ‘not guilty’ (NG)

• All have the same objective to convict the guilty, but have different info and are not sure who is guilty.

• Probability of making the right decision (for each individual) = p>1/2

• Votes are independent and sincere (not strategic)

Condorcet Jury Theorem

A jury of n (odd) members using the SMR will make the correct choice with a probability approaching 1 as n tends to infinity. The majority rule is a reliable process for making the right decision, better than requiring unanimity. General formula pictured.

Arrow’s Impossibility Theorem when there are more than 2 alternatives to choose between

Perfect preference aggregation is impossible, as no social welfare function can simultaneously satisfy the following conditions:

• Independence of irrelevant alternatives: adding new options should not affect the initial ranking of the old options

• Non-dictatorship: the collective ranking should not be determined by only 1 individual

• Pareto Criterion: If all individuals agree that one option is ranked above all others, then the social ranking should also rank this option above all others.

• Unrestricted domain: the WF should accommodate any possible individual rankings of options

• Transitivity: If society prefers A to B and B to C, then it can’t prefer C to A

Condorcet winner

A proposal that commands a simple majority against any other feasible proposal in a pairwise comparison. Aka. majority rule equilibrium (MRE).

What condition is violated in a Condorcet cycle?

Transitivity in preference rankings.

Median Voter Theory - restrictions to ensure the transitivity of the majority rule

Policy space has only one dimension (left - right)

Voters all have single-peaked preferences, with formula pictured.

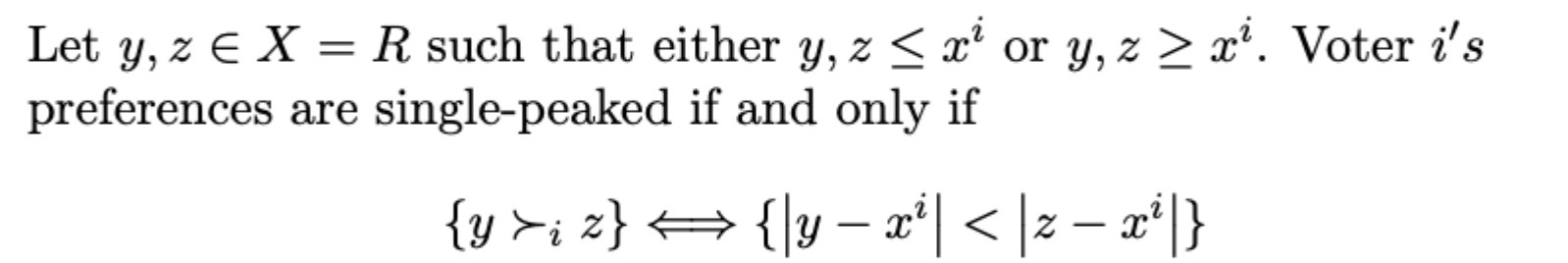
Median Voter Theory

Under the relevant restrictions, there exists a Condorcet winner that is the median position, pictured.

Contradiction proof of May’s theorem using Tie Lemma

Proof of the Median Voter Theorem

Simple: just show that the number of voters on the other side of a median vote position must be less than the number on side (inclusive of the median position itself)

Government Size example: What is the impact of expanding voter franchise?

Changes the income distribution. What matters is the relationship between the median and mean incomes. If the median drops relative to the mean, then the government will favour a higher redistributive spend. You can think of the relationship between the median and mean income as a crude measure of inequality - if inequality rises, the government will tax + spend more.

What is the timeline for the principal-agent model of lobbying

1. Contribution function is offered, specifying a contribution for each point in the policy space

2. The gov’t consults the schedule to decide which policies to compromise on, trading off contributions (which it needs to win the election) with social welfare (it’s objective function assigns greater weight to social welfare).

When lobbying the government, the SIG must get the government to implement the policy that solves the following problem

How does the principal agent game change when there are multiple SIGs

The equilibrium is a subgame perfect Nash EQ, with compensating contributions for each member, that must now also include additional payment to incentivise the government against the outside option of ignoring their policy objective to the benefit of an opposing side.

Who wins when there are more SIG's?

The government, as it can play off the SIGs against one another. If every single voter counts as an organised SIG, the end results will be the socially optimal policy, but the government will take all of the surplus out of the interaction. (Basic game theory dictates that SIGs will all try to lobby).

What are the two applications of Common Agency models that are likely to appear in the exam?

1. Externalities - EQ policy is a combination of Pigou taxation (internalise externality), a modified Pigou rule (the gov’t is paid to overinternalise the externality) and the Ramsey rule (the size of the tax depends on the elasticity of supply)

2. Trade barriers (simplified two-firm case) - Trade protection on an industry is a combination of the gov’t’s social welfare weighting, the fraction of the population who are members of SIGs, the ratio of output to imports and the absolute value of compensated elasticity of demand.

Learn these models from the notes - in particular the environment one seems the most likely to come up in the exam

The logic of collective action in the common agency model

When a potential SIG becomes an organised one depends on their ability to resolve the free rider problem.

Therefore easier for a SIG with few potential members to overcome, since monitoring potential free riders is easier.

Concentrated benefits: the small can exploit the large, as large members of the SIG have the interest to lobby and let the rest free ride.

Selective incentives: Large SIG provides group-specific public goods, along with private goods only available to fee-paying members (e.g. trade unions)