Sequences and Series

Tests for finding monotonic increase or decrease

1. Difference Test

2. Quotient Test

3. Derivative Test

When to use monotonic difference test

On sequences with rational expressions

When to use monotonic quotient test

On sequences with factorials and expressions such that 2ⁿ/n!

When to use monotonic derivative test

On sequences with an easy derivative and easy sign

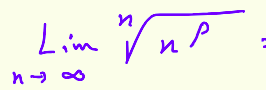
where p is any real number

= 1

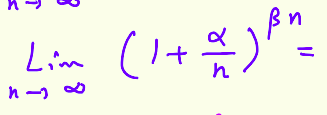
= e^ab, a,b /= 0

= 0 if -1 < r < 1
= inf if r > 1
DNE if r =< -1

When to use divergence test

1. Limit is easy to compute

2. To check for divergence (but not convergence)

When to use ratio test

If there are factorials or powers

When to use nth root test

If series contains powers (fixed or variable)

When to use comparison test

For determining absolute and conditional convergence

When to use limit comparison test

On polynomial expressions that can be replaced with their leading terms

Choices for the limit comparison test

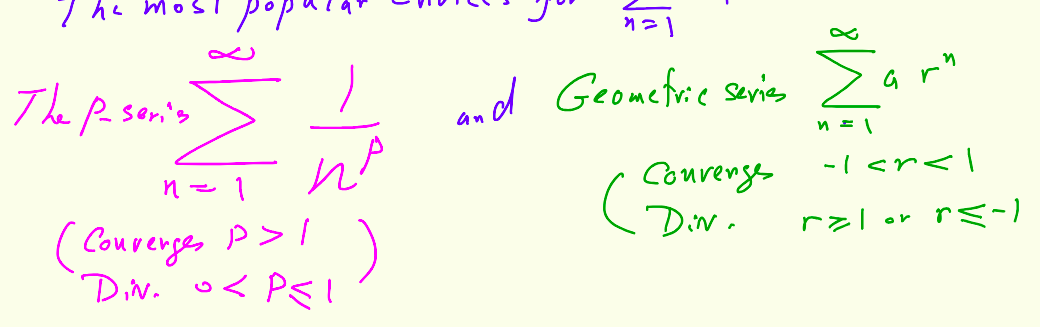
When to use limit integral test

If the following conditions are met:
1. f(x) > 0
2. f(x) is continuous on x > 1
3. f(x) is strictly decreasing on x > 1

Power Series: L

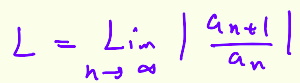
Power Series: R

R = 1/L

Power Series:Convergence

If R > 0, absolute convergence in the open interval (C-R, C+R) and diverges elsewhere
If R = 0, series only converges at x=c
If R = inf, series converges when x is real

Tests for finding series convergence

1. Divergence Test

2. Ratio Test

3. nth Root Test

4. Limit Comparison Test

5. Comparison Test

6. Integral Test

7. Alternating Series Test

When to use Alternating Test?

On series in the form (-1)ⁿa_n or (-1)^n-1a_n

Convergence condition for Alternating Test

1. Limit is 0

2. A_n is decreasing

Convergence condition for divergence test

Limit is 0 = we don’t know

Limit isn’t 0 = divergence

monotonic condition for derivative test

f’(x) > 0 = increase
f’(x) < 0 = decrease

monotonic condition for difference test

a_n+1-a_n > 0 = increase
a_n+1-a_n < 0 decrease

monotonic condition for quotient test

a_n+1/a_n > 1 = increase
a_n+1/a_n < 1 decrease

Convergence condition for ratio test and nth root test

1. 0=< Limit < 1 = Converge

2. Limit > 1 = Diverge

3. Limit = 1 = we don’t know

Convergence condition for comparison test

1. If a_n is smaller than b_n and b_n converges, a_n converges too.

2. If a_n is larger than b_n and b_n diverges, a_n diverges too.

Convergence condition for limit comparison test

If the limit of a_n/b_n /= 0 then a_n and b_n have the same behaviour

Convergence condition for integral test

1. If integral J < inf, converges

2. if integral J = inf, diverges

Convergence condition for harmonic series

1. If P>1, converges

2. If 0< P =<1, diverges

Convergence condition for geometric series

1. -1 < r < 1, converges

2. r =< -1 or r >= 1