CalcWorkshop: Solving Equations

isolating the variable

Using inverse operations to get the variable alone.

Addition and Subtraction Property of Equality

if a=b, then a+c=b+c and a-c=b-c

What is the goal for solving equations?

isolating the variable (x = )

Multiplication Property of Equality

If a = b, then ac = bc (commutative property)

Division Property of Equality

if a = b and c is not equal to 0, then a/c = b/c

if the coefficient is a fraction

multiply by the reciprocal (divide fractions)

What should you do with decimals?

change them to fractions

SCAM

Simplify with PEMDAS or the Distributive Property, Combine like terms and collect variables on one side, Addition/Subtraction, Multiplication/Division

if #( )# and/or numbers are multiples

reverse SCAM

three types of solutions

root, identity, null set

root

one solution (normal answer)

identity

all solutions, true statement (x = x)

null set

no solution (∅)

How should you move variables in an equation?

move variables to where the equation does not equal zero or where you get a positive coefficient

What is the answer if the variable disappears?

either root or null solution

Best word problem approach

read the problem carefully (what's being asked?), determine the smallest unknown, create a sidebar (translate), solve and check

past means

subtraction

future means

addition

literal equation (formula)

an equation involving two or more variables

if the variable is already isolated # = # ( )

don't distribute, reverse SCAM

how to solve absolute value equations

1) isolate the absolute value (with SCAM)
2) set up two cases: one with positive and negative answers

3) solve each case

4) substitute each solution back into original equation to check the solutions
5) if absolute value is negative, null set

6) state the final solution

if the answer is zero

only one answer

inequality

compares two quantities

How should you solve inequalities?

SCAM

When multiplying/dividing negative numbers

flip the inequality symbol

open sentence

an equation with one or more variables

solution set

The set of all values of the variable that make the equation true.

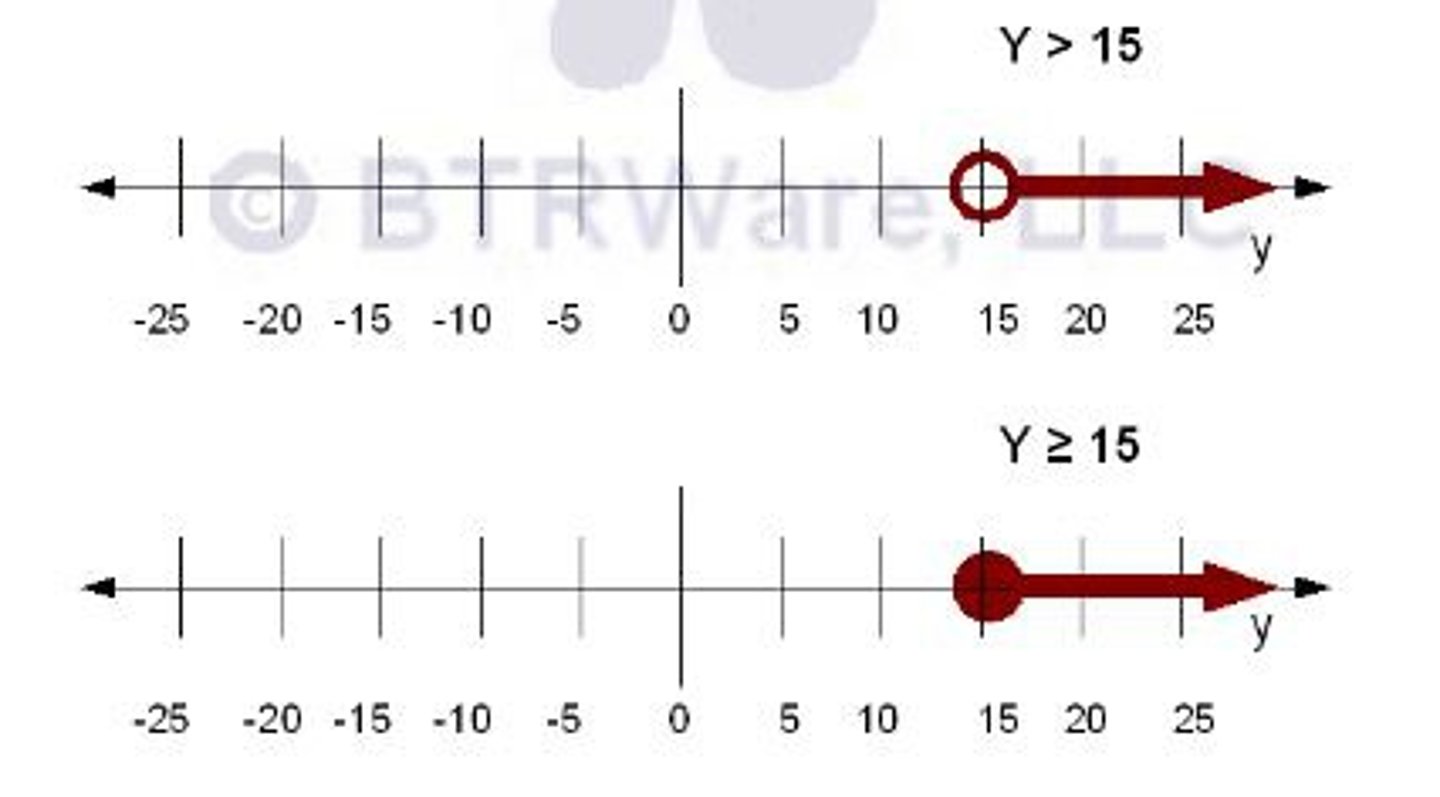
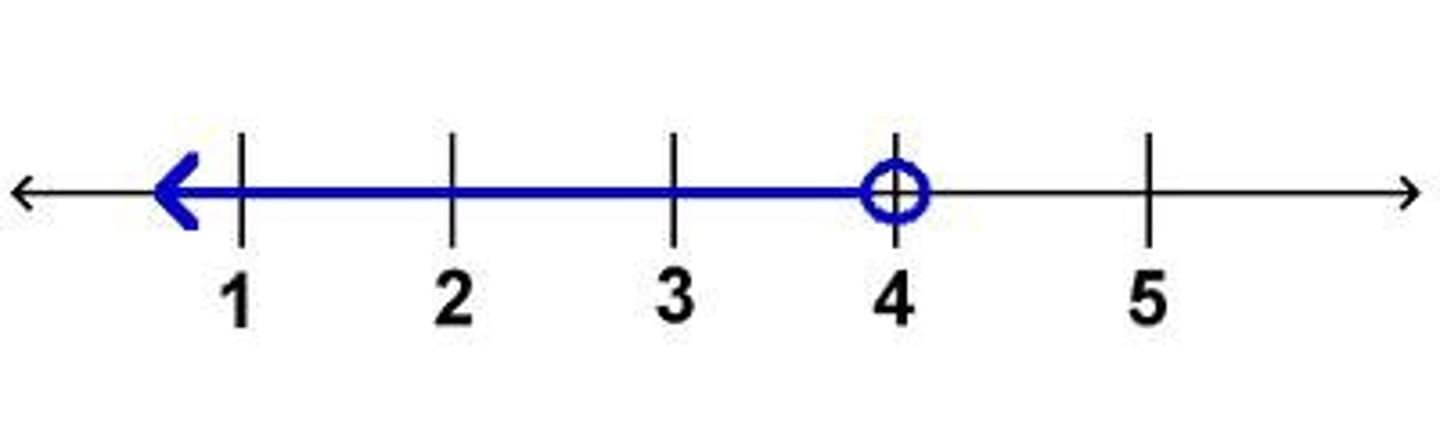
open circle

< or >

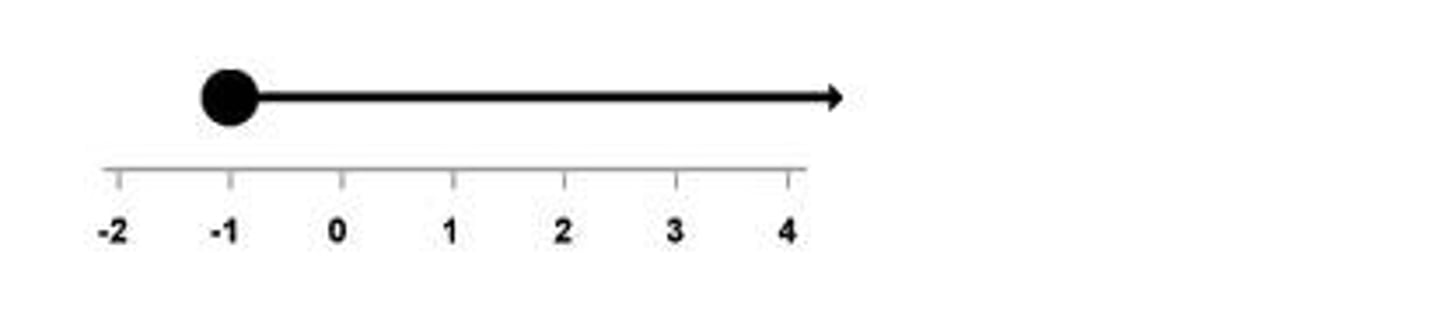
closed circle

≤ or ≥

How is an and statement written?

x is in between the values

or statement

one or both equations satisfy the equation (union)

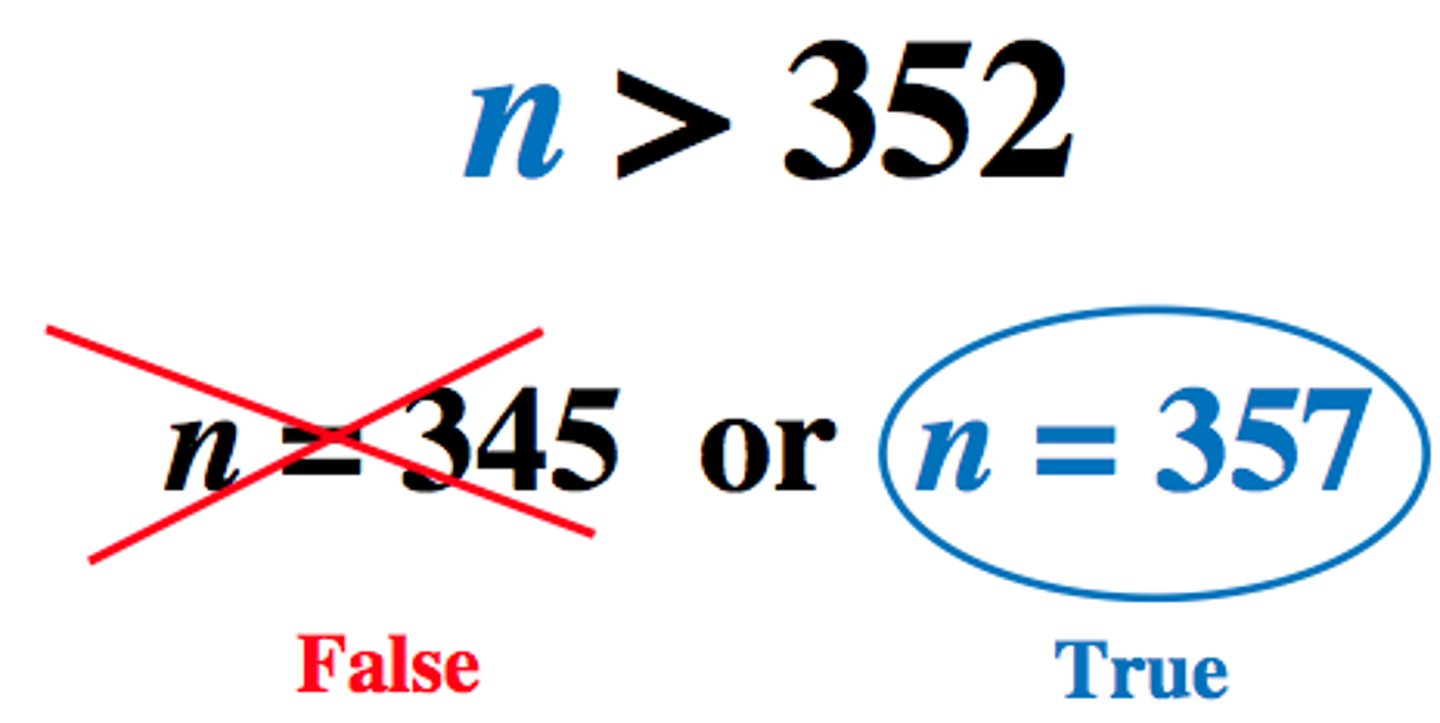
and statement

find the overlapping value (intersection) of the solution sets

How should you isolate the variable of an and statement?

isolate the variable in the middle

How should you graph and statements?

without arrows

How should you graph or statements?

with arrows

absolute value inequality and statement

less than, conjunction: two similar relationships (<, ≤)

absolute value inequality “or statement”

greater than, disjunction: two different relationships (>, ≥)

and statement inequality expression

|x-h| < a

or statement inequality expression

|x-h| > a

How to solve absolute value inequalities?

1. isolate the absolute value with SCAM
2. decide whether its an "and" or "or" statement
if its "and" change it to -a < x-h < a
if its "or" change it to x-h < -a or x-h > a
3. solve with inequality steps and graph

if the absolute value is negative

no solution (null set)

midpoint

center value

How to find the midpoint?

find the average between two values (stop and start)

distance

stop value (b) - start value (a)

midpoint formula (h)

h= b+a/2

half distance formula (k)

k= b-a/2

x = {a, b}

What are points a and b?

at least

>

no more than

≤

more/less than

><

How to solve inequality word problems?

1. read the problem carefully

2. create a sidebar

3. determine inequality (<, ≤, ≥, >)
4. solve and check (SCAM)

interval notation

(-x, x)

open interval (open circle)

(a, b)

closed interval (closed circle)

[a, b]

half-open (only one endpoint of inequality)

[), or (]