Sample Space, Relationships Among Events and Rules of Probability

2Y2 | Midterms

Probability

is used to describe the phenomenon of chance or randomness of events to occur. It does not deal with guarantees, but with the likelihood of an occurrence of an event.

If we understand how to calculate probabilities, we can make thoughtful decisions about random and unpredictable situations where multiple outcomes are possible.

Sometimes are subjective (aka theoretical or classical probability) and is based on past experience and judgment of the person to determine whether a specific outcome is likely to occur. It contain no formal calculations and differ from person to person, and they contain a high degree of personal bias. There are several methods for making subjective probability assessments:

Probabilities

Opinion polls

can be used to help in determining subjective probabilities for possible election returns and potential political candidates.

relate back to upbringing as well as other events the person has witnessed throughout his life. A production manager, for instance, might believe that the probability of manufacturing a new product without a single defect is 0.85.

Experience and judgment

Delphi method

a panel of experts is assembled to make their predictions of the future.

o Other times probabilities are objectively (aka empirical or experimental probability) based on examining past data and using logical and mathematical equations involving the data to determine the likelihood of an independent event occurring.

Probability formula

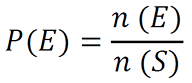
P(E)

refers a situation involving chance or probability that produces an event.

Experiments

n(S)

refers to set of all possible outcomes of an experiment, that is, any subset of the sample space.

Sample space

n(E)

refers to one or more of the possible outcomes of a single trial of an experiment.

Event

When one event occurs, it is ____________.

Simple event

When two or more events occur in a sequence, it is _____________.

Compound event

Basic Properties of Probabilities

Basic Properties of Probabilities

Property 1

The probability, P, of any event or state of nature occurring lies between greater than or equal to 0 or 0% and less than or equal to 1 or 100%. That is:

Property 2

The probability of an event will not be less than 0 because it is not possible (impossible) or can never occur. That is:

Property 3

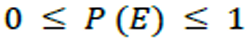
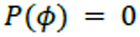
The probability of an event will not be more than 1 because 1 is certain that something will happen (sure event). That is:

The Addition Rule of Probabilities (Events Involving “OR”)

Mutually Exclusive (special addition rule)

The probability that A or B will occur is the sum of the probability of each event.

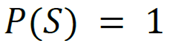
The probability that A or B will occur is the sum of the probabilities of the two (2) events minus the probability that both will occur.

Not Mutually Exclusive (general addition rule)

The Multiplication Rule of Probabilities (Events Involving “AND”)

The Multiplication Rule of Probabilities (Events Involving “AND”)

Independent Event (special multiplication rule)

Two events are independent if the occurrence or nonoccurrence of one of the events does not affect the likelihood that the other event will occur.

Dependent Event (general multiplication rule)

Two events are dependent if the occurrence of one event does affect the likelihood that the other event will occur.

Multiplication Principle of Counting

Multiplication Principle of Counting

Multiplication rule

The fundamental principle of counting is often referred to as the __________.

The multiplication principle of counting states that:

o If there are n1 possible number of outcomes/ways for event 𝐸1 ; and n2 possible number of outcomes/ways for event 𝐸2, then the possible number of outcomes/ways for both events is (n1 ∗ n2) number of outcomes/ways.

This can be generalize to E events, where E is the number of events. The total number of outcomes for E events is:

o The multiplication principle of counting only works when all choices are independent of each other. If one choice affects another choice (i.e. depends on another choice), then a simple multiplication is not right.

Permutation

is a counting technique which refers to the arrangement (or ordering) of a set of objects, from first to last, where the order in which the objects are selected does matter. In a permutation n different objects taken r at a time (where r is a subset of n), an event cannot repeat.

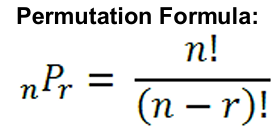
Permutation Formula

In permutation where:

_ is the number of objects to choose from

n

In permutation where:

_ is the number of objects selected

r

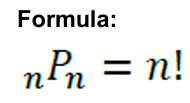
Permutation with n different objects taken all at a time

is the number of objects to arrange

n (left of P)

is the number of positions available for the objects to fill

n (right of P)

is read as “n factorial

n!

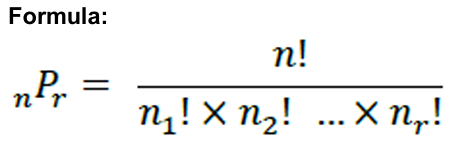
Once an event occurs in a permutation with n objects taken all at a time where some items consist of look-alikes/duplicates and rest are all different, it can occur again.

is the total number of objects

n

is the first kind

n1

nr is the last kind

nr

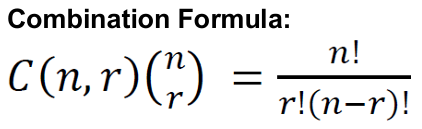
Combination Formula

is the size of the full set

n

is the number of selected set

r

is the number of set that was left

(n-r)

is a selection of objects from a collection in any order as oppose to permutations which deal with the ordered arrangements of objects.

Combination

In a combination in which r objects can be selected from a set of n objects, the selection rules are:

o the order of selection does not matter (the same objects selected in different orders are regarded as the same combination);

o each object can be selected only once; this implies that you are not allowed any repeat numbers.