Write Line Equation for Slope Y-intercept Form

Y=mx+b , where (0,b) Y-Intercept & m = Slope

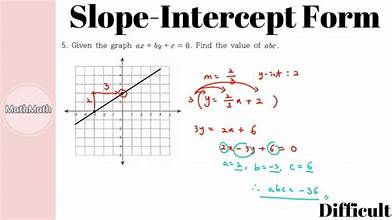
Slope-Intercept Form

is a way to express the equation of a straight line in the form y = mx + b, where m represents the slope and b represents the y-intercept.

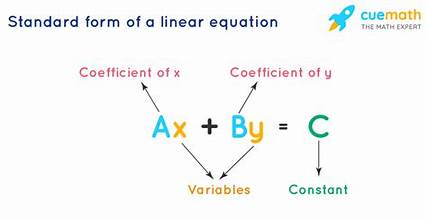
General equation for a line

is typically written as Ax + By + C = 0, representing the relationship between the variables x and y in a linear function.

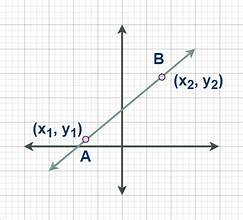
Two-Point Form

is a method to express the equation of a line using two distinct points on the line, typically written as y - y1 = m(x - x1), where m is the slope and (x1, y1) is one of the points.

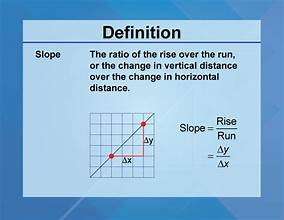
Slope

is a measure of the steepness of a line, calculated as the ratio of the vertical change to the horizontal change between two distinct points on the line.

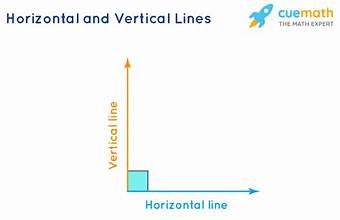
Horizontal Lines

are lines that run horizontally, having a slope of 0, and can be expressed in the form y = b, where b is the y-coordinate of any point on the line.

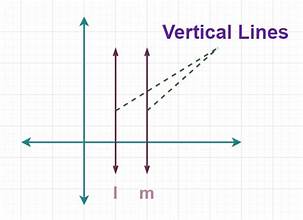
Vertical Lines

are lines that run vertically, having an undefined slope, and can be expressed in the form x = a, where a is the x-coordinate of any point on the line.

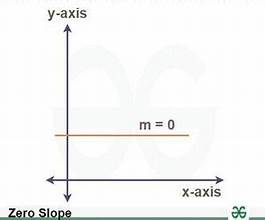
zero slope, M=0 Horizontal y=b

is the characteristic of a line that has no vertical change, indicating that it runs flat along the x-axis.

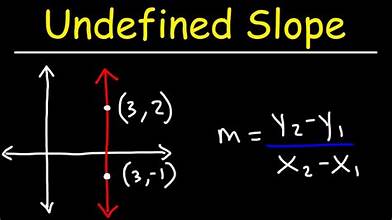
Vertical Line Equation x=a, slope undefined

is the mathematical representation of a vertical line expressed as x = a, where a is the x-coordinate of any point on the line.

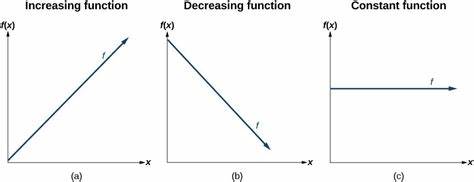
Increasing function, M>0

is a function that rises as the input increases, represented by a positive slope (M > 0) in its linear equation.

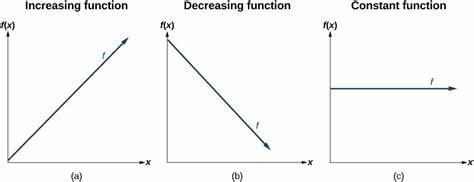
Decreasing Function M<0

is a function that falls as the input increases, represented by a negative slope (M < 0) in its linear equation.