Cryptography REAL

What is Cryptography?

Cryptography is the study of techniques for securing digital information, transactions, and distributed computations against internal or external attacks

What principle should cryptographic algorithms follow?

Kerckhoff’s Principle: the architecture and design of a security system or mechanism should be made public - no security by obscurity. This is bc an open design allows the system to be scrutinised by more people, making early discoveries and corrections of flaws much more likely. All security should follow this principle.

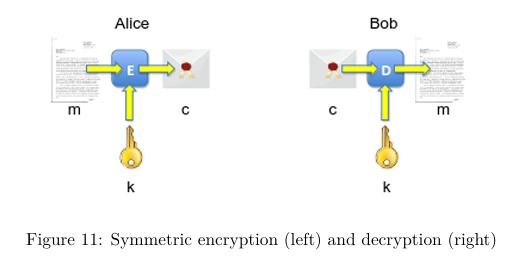
Describe symmetric ciphers

a symmetric cipher consists of 2 algorithms - one for encryption and another for decryption:

• the encryption algorithm takes a key k and a message m, producing a cipher-text c

  • the decryption algorithm takes ciphertext c and the same key k to produce the original message m

what determines whether a cryptographic scheme is secure?

a cryptographic scheme is secure under some assumptions (against a certain type of attacker). This is because some schemes are vulnerable to certain attacks but not others.

what does the attacker on a cryptographic scheme definitely know according to Kerckhoff’s Principle?

the attacker knows the encryption and decryption algorithms

what will/might an attacker know when attacking a cryptographic scheme?

• will defo know the encryption and decryption algorithms (due to Kerckhoff’s principle)

• MAY KNOW some cipher-texts c₁, …, c_n (ciphertext only attack)

• MAY KNOW some plain-text/cipher-text pairs (m₁, c₁), …, (m_n, c_n) s.t. c_i = E(k, m₁) (known plaintext attack)

• MAY HAVE ACCESS TO an encryption oracle

  • can see the results of encrypting messages m₁, …, m_n of their choice (chosen plaintext attack)

• MAY HAVE ACCESS TO a decryption oracle

  • can see results of decrypting some ciphertexts c₁, …, c_n of their choice (chosen ciphertext attack)

what is a ciphertext only attack?

where the attacker knows some cipher-texts c₁, …, c_n

what is a known plaintext attack?

where the attacker knows some plain-text/cipher-text pairs (m₁, c₁), …, (m_n, c_n) s.t. c_i = E(k, m_i)

what access does the attacker have in a chosen plaintext attack?

an encryption oracle

• can see the results of encrypting messages m₁, …, m_n of their choice

what access does the attacker have in a chose ciphertext attack?

a decryption oracle

• can see the results of encrypting ciphertexts c₁, …, c_n of their choice

what levels of computational power might an attacker have?

attackers may have varying levels of computational power, such as unlimited, polynomial, or realistic (currently <= 2⁸⁰)

describe a brute-force attack

“brute-force attack” can be applied to any cryptographic scheme. It involves trying all possible keys k ∈ K. This requires some knowledge about the structure of the plain text.

Making an exhaustive search should be infeasible UNLESS the attacker has unlimited computational power. K should be sufficiently large, and keys should be sampled uniformly from K

Describe substitution ciphers

A substitution cipher relies on a shared secret between the person sending the message and the person receiving the message. In this case, the secret is a permutation π of the set of characters. Encryption involves applying this mapping π to each element of the plain text.

E(π, c₁ … c_n) = π^-1(c_n)

What are substituion ciphers weak to?

frequency analysis

XOR is involutory. what does this mean?

f(f(x)) = x so applying XOR to an XOR will return the initial input.

Describe OTP

In a one-time pad, the length of the message m ∈ M, ciphertext c ∈ C, and the key k ∈ K are equal. M = C = K = {0, 1}ⁿ. OTP satisfies perfect secrecy. OTP is malleable.

Describe OTP encryption

Encryption in a one-time pad is a process that takes a key and a message, and produces the ciphertext by performing XOR on the key and the ciphertext

∀k ∈ K.∀m∈M.E(k,m)=k⊕m= c

Describe OTP decryption

because XOR is involutory, decryption just involves performing the same process as encryption (XOR), but this time with the ciphertext and the key.

∀k ∈ K.∀m∈M.D(k,c)=k⊕c= m

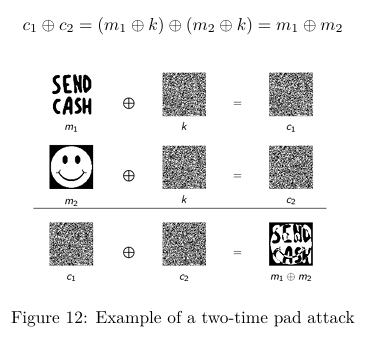
What attack works on the OTP? Describe this.

Two-time pad attack. This exploits the fact that the key is encoded already in ciphertexts and can be removed to give 2 plain-texts meshed together. Bc plaintext data is much more predictable than random data, we can often get most of the original messages out from doing this.

c1 ⊕c2 = (m1 ⊕k)⊕(m2⊕k)=m1⊕m2

OTP satisfies perfect secrecy. What does this mean?

A cipher (E, D) over (M, K, C) satisfies perfect secrecy if:

for all messages m₁, m₂ ∈ M of the same length (|m1| = |m2|) and for all ciphertexts c ∈ C:

|Pr(E(k, m1) = c) - Pr(E(k, m2) = c)| <= ϵ where k ← r ← K and ϵ is some negligible quantity.

IN ENGLISH: the probability of encrypting any one message and getting c should be roughly equal to that of encrypting another and getting c, where keys are drawn uniformly from the key-space.

Perfect secrecy DOES NOT capture all possible attacks.

OTP is malleable. what does this mean?

a cipher is malleable if it is possible to turn some ciphertext c₁ into some other ciphertext c₂ which decrypts to a related plain-text.

e.g."TRANSFER $00100.00 TO ACCOUNT #199."→"TRANSFER $99999.99 TO ACCOUNT #227."

a malleable cipher might allow an attacker to change details of messages (as above)

What are some limitations of OTP?

1. the key in OTP has to be as long as the plaintext, which is substantially larger than other methods

2. generating truly random numbers is difficult. the key shouldn’t be guessable by attackers, but if the key is not truly random, frequency analysis may be possible

describe cryptographic hash functions

a cryptographic hash function takes messages of arbitrary length and retruns a fixed-size bit string such that any change to the data will (with a very high probability) change the corresponding hash value.

H : M → T

A cryptographic hash function H:M→T is a function that satisfies 4 properties:…

1. |M| > > |T|

2. It’s easy to compute the hash value for any given message

3. It’s one-say, meaning it’s hard to retrieve the message from its hashed value

4. It’s collision-resistant, meaning it’s hard to find 2 different messages with the same hash value. Hwv, because the domain is so much larger than the range, collisions are unavoidable

Are collisions avoidable in cryptographic hash functions?

No, collisions are UNavoidable in cryptographic hash functions because the domain is so much larger than the range (|M| > > |T|)

Describe collision-resistant functions

A function f is collision resistant if there are no efficient algorithms that can find 2 messages m1 and m2 such that f(m1) = f(m2)

What are some coolision resistant functions?

1. the successor function in N is collision resistant - the predecessor of a positive integer is unique

2. multiplication of large primes is collision resistant - every positive integer has a unique prime factorisation

what kind of cryptographic hash functions should we use in new projects?

SHA-256, SHA-512, or SHA-3

What are some key applications of cryptographic hash functions? [4]

1. chf’s allow a participant to commit to a value v by publishing the hash H(v) of this value but revealing v only later

2. hashes are sometimes posted along with files on read-only spaces to allow verification of file integrity

3. instead of storing passwords in plain-text only, the hash digest of each password is stored. to authenticate a user, the password presented by the user is hashed and compared to the stored hash.

4. Key Derivation Functions (kdfs) use chfs to stretch a password, derive multiple (new) keys from one key, turn a passphrase into smth cryptographically strong

Cryptographic Hash Functions are used to build: [3]

• MACs (message authentication codes)

• block ciphers

• PRG

What is a MAC address?

A MAC address is a 48-bit number usually represented in hex (e.g. 00-1A-92-D4-BF-86); it is a hardware ID built into a NIC (network interface card). Most network interfaces come with a predefined MAC address.

The first 3 octets of any MAC address are IEEE-assigned Organisationally Unique Identifier (OUI) (they are only provided to the associated company, e.g. 00-1A-92 means it belongs to ASUSTek).

The final 3 octets of any MAC address can be assigned as the organisation pleases, with the only constraint being that all MAC addresses are unique globally/ and no 2 devices from the same manufacturer share the same 48-bit value.

What are MAC addresses used for?

Local network communcation (within the same LAN), NOT For routing on the internet

what does H : M → T mean? (describing a cryptographic hash function)

H takes a message from M and produces a hash value in T, where H is the hash function, M is the set of all possible messages (inputs), and T is the set of all possible hash outputs (digests)

Describe the Birthday Attack

Given a cryptographic hashing function H : M → {0, 1}ⁿ (where |M| >> 2ⁿ), to find collision in time O(2^n/2):

1. choose 2^n/2 random messages in M: m₁, …, m_2^n/2

2. For i = 1, …, 2^n/2, compute t_i = H(m_i)

3. If there’s a collision (∃i,j. t_i = t_j), return (m_i, m_j), otherwise go to 1

Because of the birthday paradox, we know that for any value of n > 1.2 x sqrt(N) (where N is the max. possible value of n), the probability of a collision > 50%

What does the birthday paradox state?

The birthday paradox states that for a random sample of variables r₁, …, r_n ∈ {1, …, N}, the probability of a collision for n = 1.2 x sqrt(N) is greater than 50%

Describe the Merkle-Damgard Construction

Given a compression function h:T x X → T, we can chain together applications of this function applied to subsections of the message to get a complicated hash.

The fixed initialisation vector (IV) goes into the first T input, and then X is a sub-block of m. Each is of equal length - the last block is padded to fill it out. IF H is built using M-D from h, then if H admits a collision, so does h. (this H is an example of a block cipher)

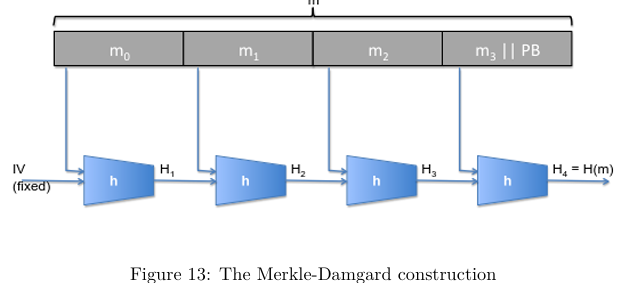
if hash function H is built using Merkle-Damgard from h, what happens if H admits a collision?

if H admits a collision, so does h.

what is a block cipher?

a block cipher is any cipher which operates on fixed-size inputs, or “blocks”, producing an output of equivalent size. Typically the blocks are 128 or 256 bits. Merkle-Damgard constructions are an example of a block cipher.

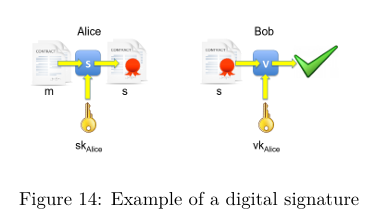
What is the point of digital signatures?

Digital signatures aim to enforce data integrity and origin authenticity in the public-key setting

A digital signature system is composed of 3 algorithms, describe these.

(G, S, V)

• G: () → K x K ; the key generation algo G produces a pair of key, on of which is for signing and the other is for verification

• S: K x M → S ; the signing algo S creates a signature from the signing key and the message we want to send

• V: K x M x S → {⊤,⊥} ; the verification algo V takes the second key, the message, and the signature and verifies if the signature is correct

What is the result of a digital signature?

For any pair of keys s_k and v_k, and any message m, V(v_k, m, S(s_k, m)) = T

Digital signatures have a couple of advantages over MAC. What are these?

1. Digital signatures are publicly verifiable - anyone can verify them

2. Digital signatures are transferrable - due to public verifiability

3. Digital signatures provide non-repudiation - if a document is signed by a user, they cannot later deny it

Any good digital signature scheme should satisfy…

existential unforgeability

What is data integrity?

data integrity is the principle that data should be untampered and uncorrupted

What is authenticity?

authenticity is the ability to know with certainty the identity of a communicating entity

Is RSA symmetrical or asymmetrical?

RSA is an asymmetric encryption algorithm

How are signatures in RSA generated?

Signatures in RSA are generated using large primes and modular arithmetic.

G_RSA() = (p_k, s_k) where p_k = (N, e) and s_k = (N, d), where N = p DOT q with p and q being random primes and c, d ∈ Z and d ≡ 1(mod ϕ(N))

M = C = Z_N

Signatures are performed like so: S_RSA(s_k, x) = (x, x^d(mod N))

How does verification work in RSA?

Verification (V_RSA(p_k, m, x)) involves checking if m = x^e(mod N). If it is, then it returns T, otherwise returning ⊥.

What do digital signatures provide that RSA signatures don’t?

Existential unforgeability.

What is existential unforgeability?

Given some messages m₁, …, m_n (chosen by an adversary) and their corresponding signatures S(k_s, m₁), …, S(k_s, m_n), it should be hard to compute a valid pair (m, S(s_k, m)) without knowing s_k for any of the chosen messages.

How can an attacker exploit RSA?

Since RSA signatures don’t provide existential unforgeability, given 2 valid signatures σ₁ = M^d₁ mod n and σ₂ = M^d₁ mod n for messages M₁ and M₂, the attacker can exploit the homomorphic properties of RSA.

σ = σ₁ DOT σ₂ mod n = M^d₁ DOT M^d₂ mod n = (M₁ DOT M₂)^d mod n

This σ is a new signature which is valid for the message M₁ DOT M₂

How can we securely use RSA?

To securely use RSA, we apply a hash function first. Encryption becomes S_RSA(s_k, x) = (x, H(x)^d (mod N)), and decryption involves hashing the message before comparing it - checking if H(m) = x^e(mod N)

What are MACs?

MACs are message authentication codes.

when encrypting with a cipher - like the one-time pad - messages which are intercepted can be easily altered. we want to prevent this, guaranteeing message integrity. a MAC is a pair of algorithms (S, V) defined over (K, M, T) where S generates a tag and V verifies that the tag is the same when the message is recovered:

S : K x M → T

V : K x M x T → {T, ⊥}

This makes it extremely hard to compute a valid pair (m, S(k, m))

What is the goal of MACs?

when encrypting with a cipher - like the one-time pad - messages which are intercepted can be easily altered. we want to prevent this, guaranteeing message integrity.

Given a block cipher, how can we build a MAC? why would we do this?

Given a block cipher (E, D) we can build a MAC (S, V) as follows:

S(k, m) = E(k, m)

V(k, m, t) = if (m ≡ D(k, t)) then return T else return ⊥

with this, we can construct MACs for messages longer than a single block

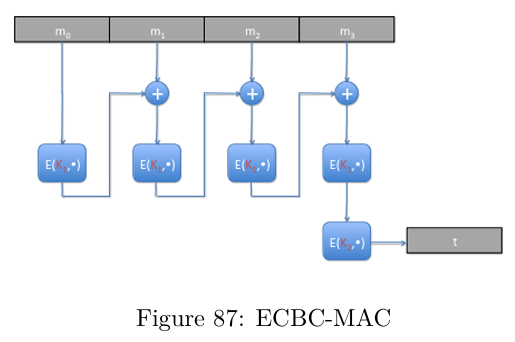
Describe ECBC-MAC

The encryption algo E is a block cipher.

ECBC-MAC is a function which takes a pair of keys K1, K2 ∈ K and a message m of arbitrary length, and gives an encrypted message of equivalent length. Each block depends on the previous block being properly encrypted. They are combined using XOR

Describe PMAC

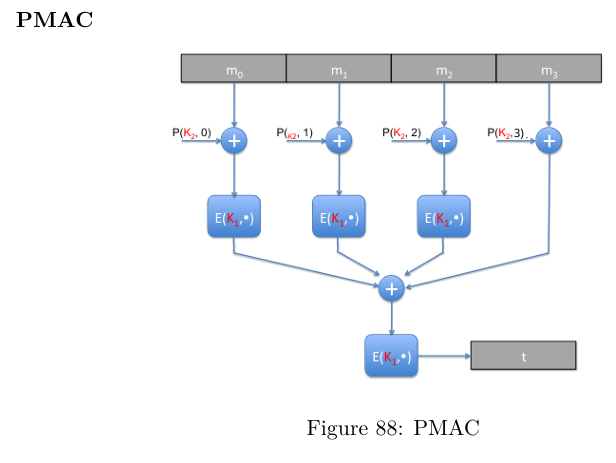
The encryption algorithm E is a block cipher, and P : K x N(aturalno.s) → {0, 1} is any easily computed function.

PMAC is a function which takes a pair of keys K1, K2 ∈ K and a message m of arbitrary length, and gives an encrypted message of equivalent length.

Each block is calculated separately, the final block is padded and then XOR-ed directly with the results of encrypting the other blocks - then the result is encrypted.

Describe HMAC

HMAC is a MAC built using cryptographic hash functions. It is constructed using XOR and the regular binary OR operator (||). HMAC(k, m) = H(k ⊕ OP || H(k ⊕ IP || m)) where IP and OP are publicly known padding constants.