Precalc/Trig Chapter 6: graphing/inverse trig, verifying identities, laws of sin+cos

for the class at IWA; includes info from previous chapter to make sure everyone knows it for our test

general equations for sine and cosine graphs

general equations for sine and cosine graphs

f(x) = Asin(Bx-C)+D and Acos(Bx-C)+D

What does A mean in an equation?

Amplitude (how far the graph goes up, how far the graph goes down)

What does B mean in an equation?

Frequency (number of cycles in 2pi; when B=1 there is one cycle in 2pi)

What does D mean in an equation?

vertical shift

What is the phase (horizontal) shift in a sin/cos equation?

C/B

Period in a sin/cos graph

2pi/B

To graph a sin/cos graph…

divide the period by four, giving you the minimums, maximums, and intercepts

Range

y values

domain

x values

How do you find a period in a graph?

count length of one cycle (one up, one down)

How do you find B from a graph

set 2pi/B equal to the period and solve

If the B value in a tangent or cotangent graph is 1, the period is…

pi

to graph tangent or cotangent, fine the values where the function is —. These will be — — —.

undefined, vertical asymptote values

general equations for tan and cot graphs

y=tanx and y=cotx

What is the period in a tan/cot graph if B is NOT 1?

pi/B

For tangent, set Bx = —, —, — to find vertical asymptotes

-pi/2, pi/2, 3pi/2

For cotangent, set Bx = —, —, — to find vertical asymptotes

-pi, 0, pi

To graph a csc or sec graph…

use the reciprocal graph as a guide. The x intercepts will create vertical asymptotes on the reciprocal graphs

On csc and sec graphs, the x-ints from the guide graphs are…

vertical asymptotes

On csc and sec graphs, the relative max/mins from the guide graphs are…

vertexes

Range restrictions for inverse trig

sin and csc: q1 and q4

tan and cot: q1 and q4

cos and sec: q1 and q2

y=ArcSinx is the same as…

y=sin^-1x

each inverse trig expression has only — —-, which MUST be in the — restriction.

one answer, range

for special angle value expressions, evaluate the inside inverse trig function for the —, then find the — —.

angle, trig ratio

For trig values with numbers not on the unit circle, — — — from the inverse trig statement, then find the — —.

draw the triangle, trig ratio

when simplifying a trig function in terms of x, draw a triangle, fill in the missing side with a — — and find the trig ratio

x expression

reciprocal identity of sinx

1/cscx

reciprocal identity of cosx

1/secx

reciprocal identity of tanx

1/cotx

reciprocal identity of cscx

1/sinx

reciprocal identity of secx

1/cosx

reciprocal identity of cotx

1/tanx

sin²x + cos²x= —

1

1+tan²x= —

sec²x

1+cot²x= —

csc²x

1-sin²x and sin²x-1= —

cos²x

1-cos²x and cos²x-1= —

sin²x

even-odd identity rules

cos and sec will be pos with a negative x input (will still be positive if +x). Other ratios will be negative with a negative x.

sin(A+B)

sinAcosB+cosAsinB

sin(A-B)

sinAcosB-cosAsinB

cos(A+B)

cosAcosB-sinAsinB

cos(A-B)

cosAcosB+sinAsinB

(note: mrs. rich said this won’t be on the test, but it’s here for memorization.)

tan(A+B)

tanA+tanB/1-tanAtanB

(note: mrs. rich said this won’t be on the test, but it’s here for memorization.)

tan(A-B)

tanA-tanB/1+tanAtanB

know what functions are positive in what quadrants

q1: all

q2: sin csc

q3: tan cot

q4: cos sec

what would you do when given an equation like sin(pi/3 + pi/4)?

write out equation and use triangles to find values. then solve.

what would you do when given an equation like sin(5pi/12)?

find numbers that add or subtract to what is in parenthesis and also simplify to /4, /3, or /6. Then solve as if you were given the numbers.

If given some ratios of A and B in certain quadrants, draw — and then — as normal.

triangles, solve

sin2x

2sinxcosx

cos2x

cos²x-sin²x

(note: mrs. rich said this won’t be on the test, but it’s here for memorization.)

tan2x

2tanx/1-tan²x

In a question where you are given a trig ratio and its quadrant, you would…

draw the triangle and plug the subsequent values/ratios into what the question asks for

angles and measurements for 30/60/90 triangle

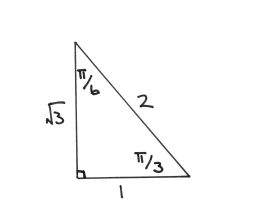
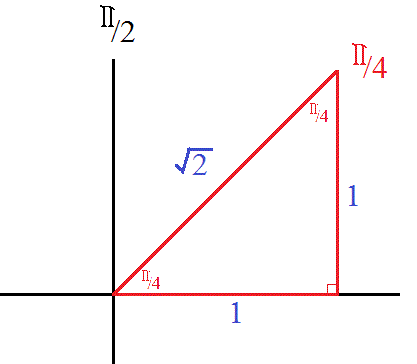
angles and measurements for 45/45/90 triangle

sin in terms of x,y

y

cos in terms of x,y

x

tan in terms of x,y

y/x

csc in terms of x,y

1/y

sec in terms of x,y

1/x

cot in terms of x,y

x/y

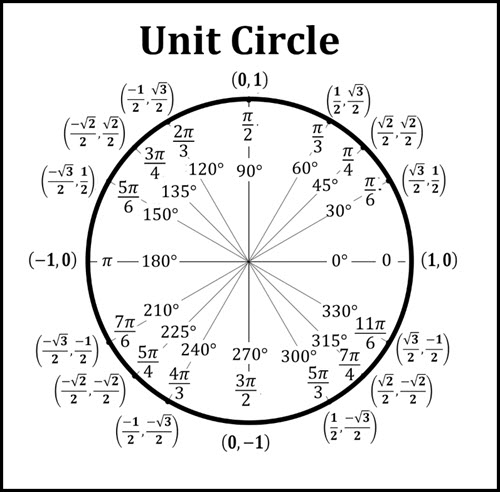
unit circle points and angles

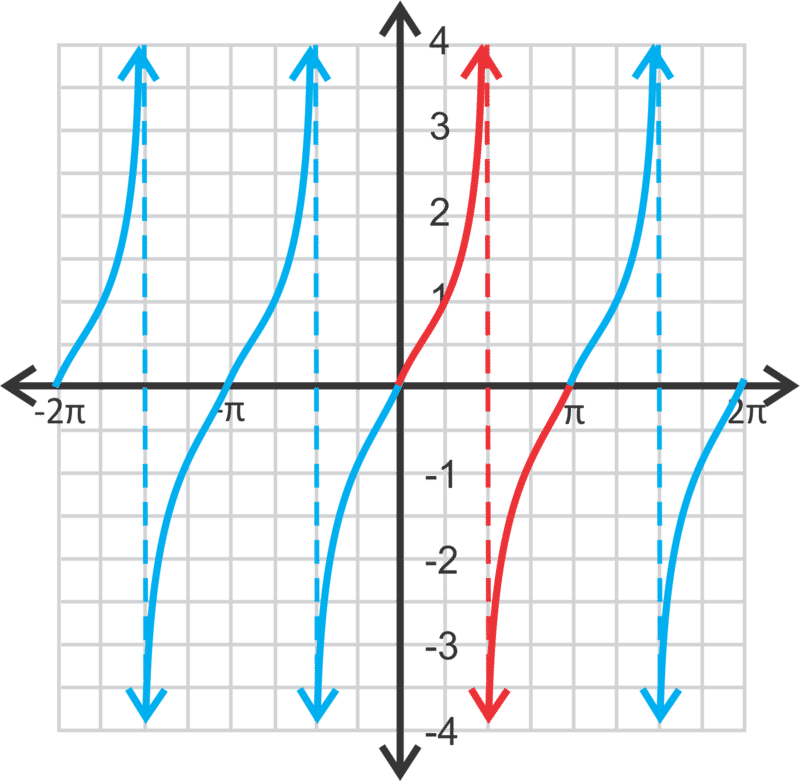
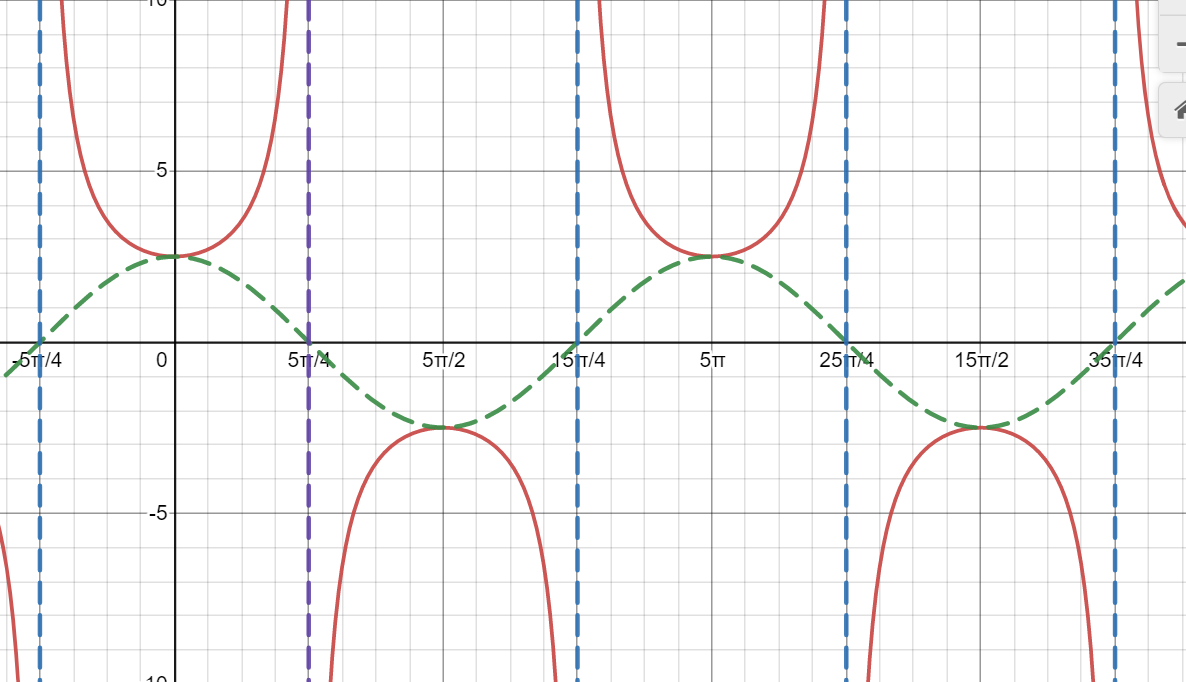
tangent graph

cotangent graph

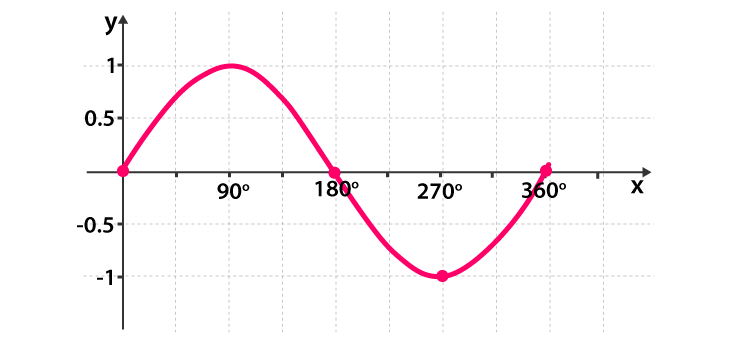
sin graph

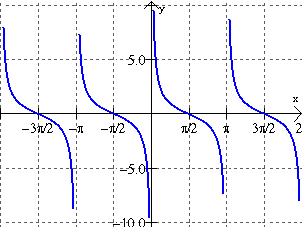
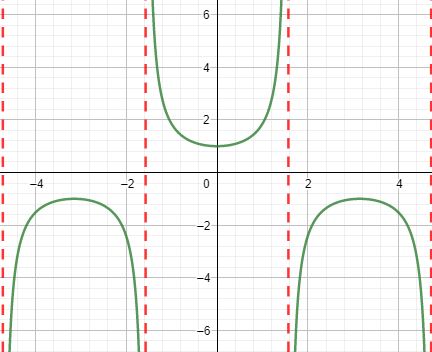
csc graph

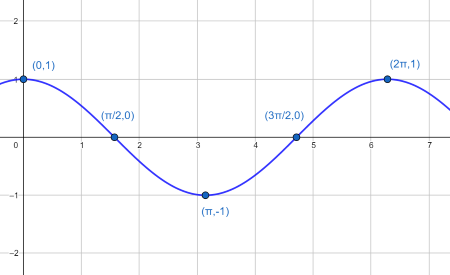
cos graph

sec graph

oblique triangle

triangle that does not contain a right angle

has either three acute angles or two acute angles and one obtuse angle

To use the law of sines…

need two angles and the side across from one of the angles OR two sides and the angle across from one of the sides

Only — ratios are used to solve for one unknown part of the triangle when using the law of sines.

two

ambiguous case

it’s possible to have 0, 1, or 2 triangles for two sides and one angle

In the ambiguous case, you have 0 triangles when…

sin > 1

In the ambiguous case, you have 1 triangle when…

adding up the given angle and ang equal to one you solved for is > 180

In the ambiguous case, you have 2 triangles when…

adding up given angle and ang equal to one you solved for is < 180

Area for oblique triangle

½ bc SinA, ½ ab SinC, ½ ac SinB

law of cos is needed to solve for the missing part for:

SAS, SSS

once missing part of oblique triangle is found with law of cos, — — — can be used

law of sines

cos of pi/6

square root of 3/2

sin of pi/6

1/2

tan of pi/6

square root of 3/3

sin of pi/4

square root of 2/2

cos of pi/4

square root of 2/2

tan of pi/4

1

cos of pi/3

1/2

sin of pi/3

square root of 3/2

tan of pi/3

square root of 3