Permutations, Induction

product principle

if a procedure can be divided into two tasks and there exists n1 ways to accomplish the first task and n2 ways to accomplish the second task once the first is done, then there exists n1 * n2 WAYS to accomplish the ENTIRE procedure

• think of a truth tree

permutation

a PERMUTATION of a set of distinct objs is a WAY to order these objs

r-permutation

an ordering of r elements from a set containing n distinct elements

P(n,r)

denotes the number of r-permutations (diff orderings) of a set of n elements

P(n,n)

denotes the number of permutations of a set of n elements

(the orderings all have a length of n elements)

r-combination

a subset of a set S of size r (order of elements in subset does not matter)

ex: list all the subsets of S = {1, 2, 3, 4} which contain exactly 3 elements

C(n, r)

denotes the number of r-combinations of a set containing n elements

• in other others, it is the num of subsets T of a set S such that the cardinality of T = r and the cardinality of S = n

formula for C(n, r)

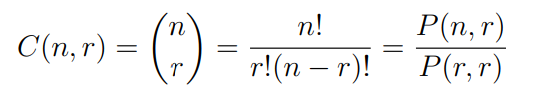
permutations with repetitions (ex: PEPPERONI)

• temporarily treat the repeating letters as if they’re distinct: permutations of PEPPERONI = 9!

• then, divide out the “repeat” permutations (ex: EPPROPENI would be repeated) by dividing 9! by 3! (the num of P’s) and 2! (the num of E’s)

• 9!/(3!*2!) is the final answer

C(n, r) * P(r, r) =

P(n, r)

The photographer wants to select 5 people and align them for a photo. How many possibilities do they have, given that A and B have to be next to each other in the picture?

• treat AB or BA as if it’s one entity

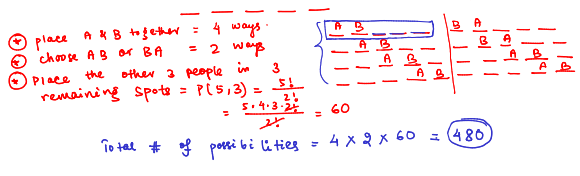
sum principle

if a task can be accomplished in n1 ways and a second task can be accomplished in n2 ways, and these two tasks cannot be accomplished simultaneously (cannot be accomplished one after another, can only do EITHER one or the other), then there are n1 + n2 ways to accomplish one task or the other

• commonly applied to situations that must be split into several possible CASES

inclusion-exclusion principle: calculating the number of distinct elements in a union set

|A ∪ B| = |A| + |B| − |A ∩ B|

• the number of distinct elements in a union set is = (num of distinct of elements of A) + (num of distinct elements in B) - (num of elements that A and B have in common)

inclusion-exclusion principle: calculating the number of distinct elements the COMPLEMENT of a union set of A + B

|(A ∪ B)’| = |U| − |A ∪ B| = |U| − (|A| − |B| + |A ∩ B|)

reminder that |A| − |B| + |A ∩ B| = |A ∪ B|

inclusion-exclusion principle w three sets

|A ∪ B ∪ C| = |A| + |B| + |C| − |A ∩ B| − |A ∩ C| − |B ∩ C| + |A ∩ B ∩ C|

induction

method for proving that a mathematical statement P(n) is true for EVERY NATURAL NUMBER n (1 to infy)

sum of the first n ODD POSITIVE INTS =

n²

ex: first 3 odd nums: 1, 3, 5

1 + 3 + 5 = 9

which is 3²

principle of mathetical induction

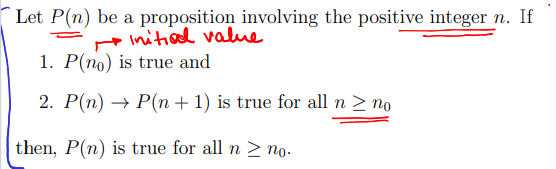
steps to writing a proof by induction

1. For n ∈ N, define the proposition P(n).

2. For the initial value, n0, we show P(n0) is true.

3. Let k ≥ n0, and suppose P(k) is true.

4. We show P(k + 1) is true (basically a proof structure of P(k) → P(k+1)

5. We conclude that since P(n0) is true and P(k) → P(k + 1) is true for all k ≥ n0, then P(n) is true for all n ≥ n0.

strong induction concept

• a variation on the principle of induction

strong induction requirements

proof by strong induction steps

defn of prime num

a num n >= 2 is PRIME if its only positive divisors are 1 or n (itself)

defn of composite num

• a num that is NOT prime

• given a number n, there exists a, b (belonging to ints) s.t a > 1 and b < n and n = ab

pigeonhole principle application

N = k(r - 1)

where N = total num of objs

k = number of boxes/categories/subsets

r = ensured by the total num of objs that one box contains exactly r objs