CH. 3 DISPLAYING AND SUMMARIZING QUANTITATIVE DATA

What is quantitative data?

It’s data that consists of variables that measure numerical quantities 

What are 2 major ways we can describe quantitative data? Using what?

plots, numerical summaries 

What are the 2 types of plots we can use to describe quantitative data?

histogram, boxplot 

What are the 3 types of numerical summaries we can use to describe quantitative data?

mean, median, range, etc.

What type of categories do histograms create? 

artificial categories for values of quantitative variable

What do you call these artificial categories that these histograms create?

bins or classes

Fill in the blanks.

Pretend variables is categorical & create _______.

bar-plot

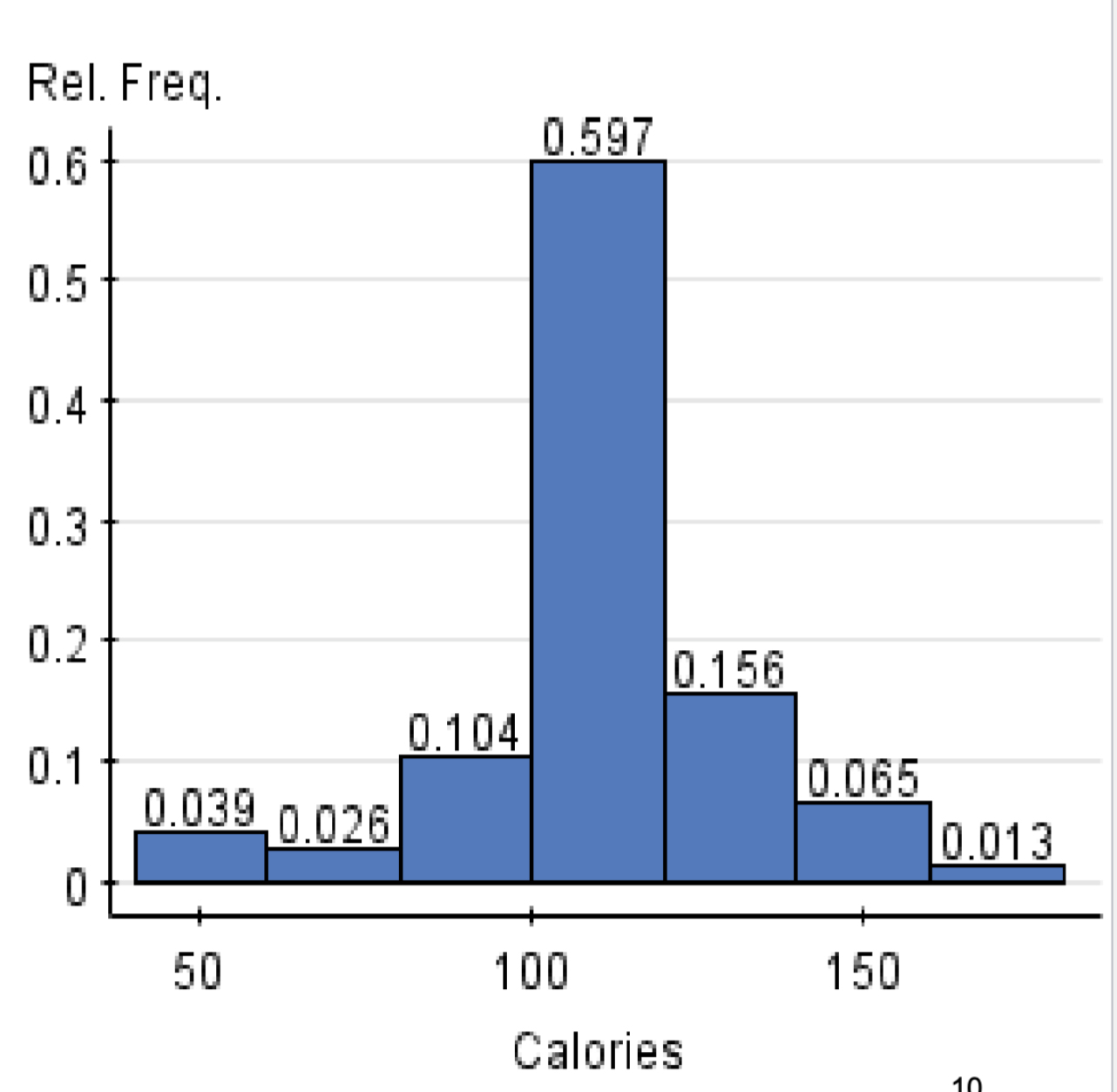
What type of graph is this in the image shown?

relative frequency histogram

What are the 2 major features that distinguish bar-plot from histogram?

• Categories (classes)
  are ordered

• No gaps between
  bars (unless freq.=0)

For any quantitative variable, what are 3 aspects we look at to describe the overall pattern of it’s distribution?

• shape

• centre

• spread

What do you look at when you see the shape of the distribution?

the modality

What does modality refer to?

the number of modes or peaks in the data set distribution 

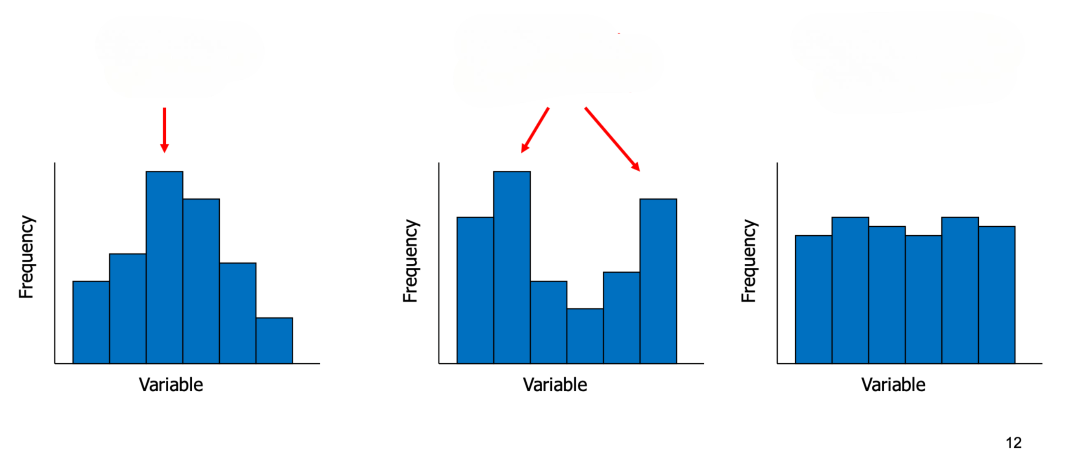
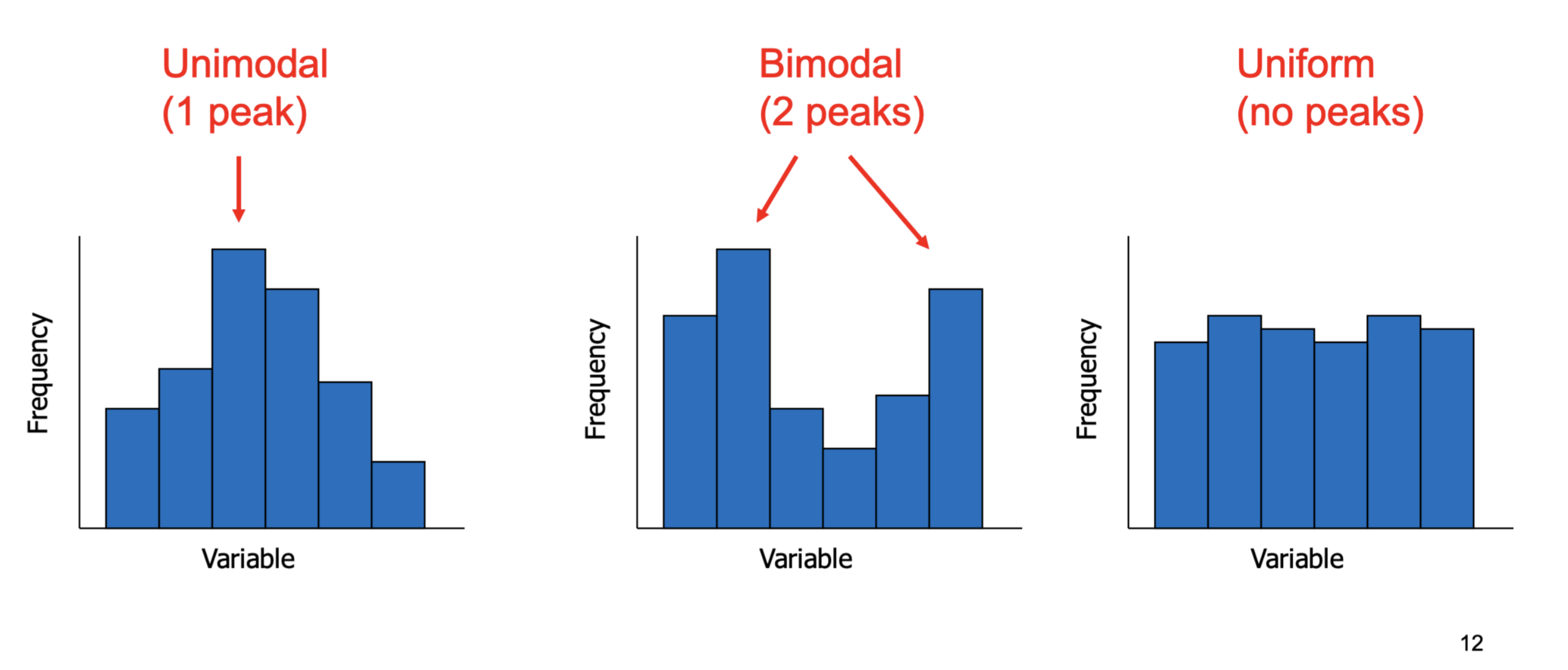
What are the 3 different types of modality (shape of distribution)?

1. unimodel

2. bimodel

3. uniform

What are the 4 factors you must consider when looking at the shape of the distribution?

1. modality

2. symmetry

3. skeweness

4. outliers

Looking at the shape of the distribution, when do we call a distribution “symmetric”?

if, when we draw a vertical line down its center, the two sides are similar in shape and size

When do we call a shape of distribution towards being “skewed”?

When the graph is a unimodal distribution with one
tail longer than the other.

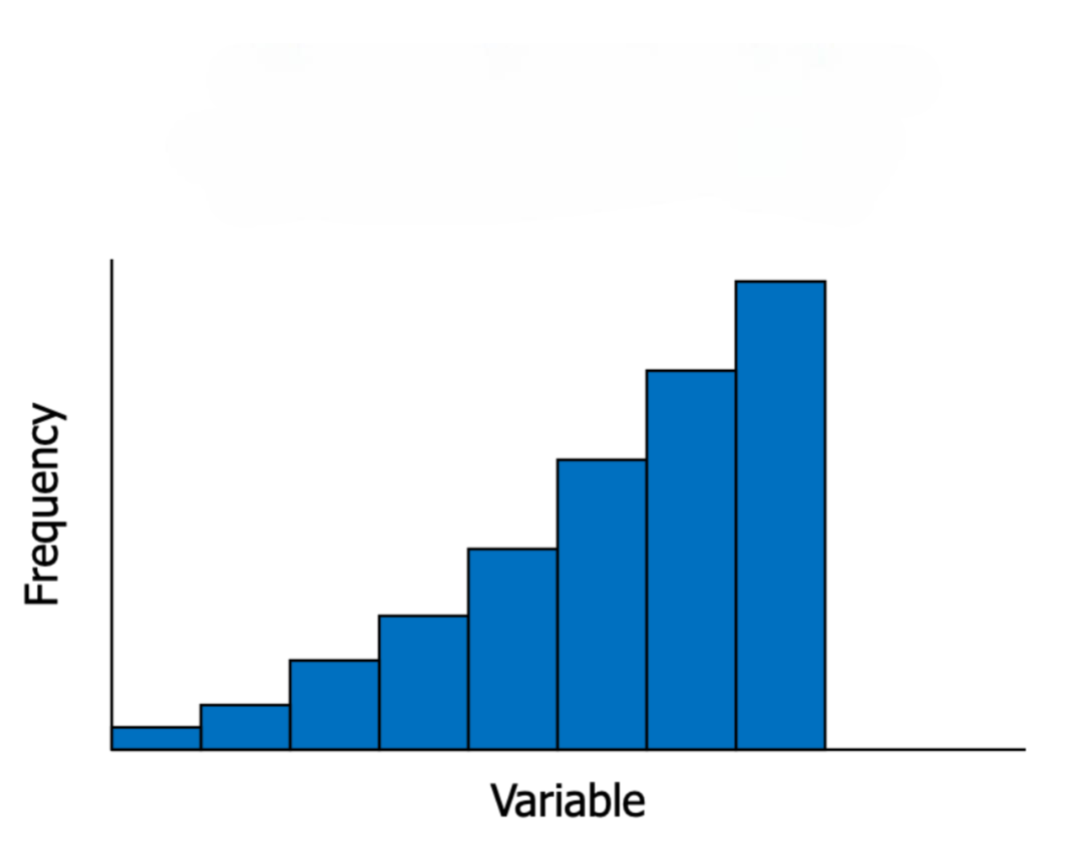
How would you describe the shape of the distribution in the provided image?

skewed to the left (negatively skewed)

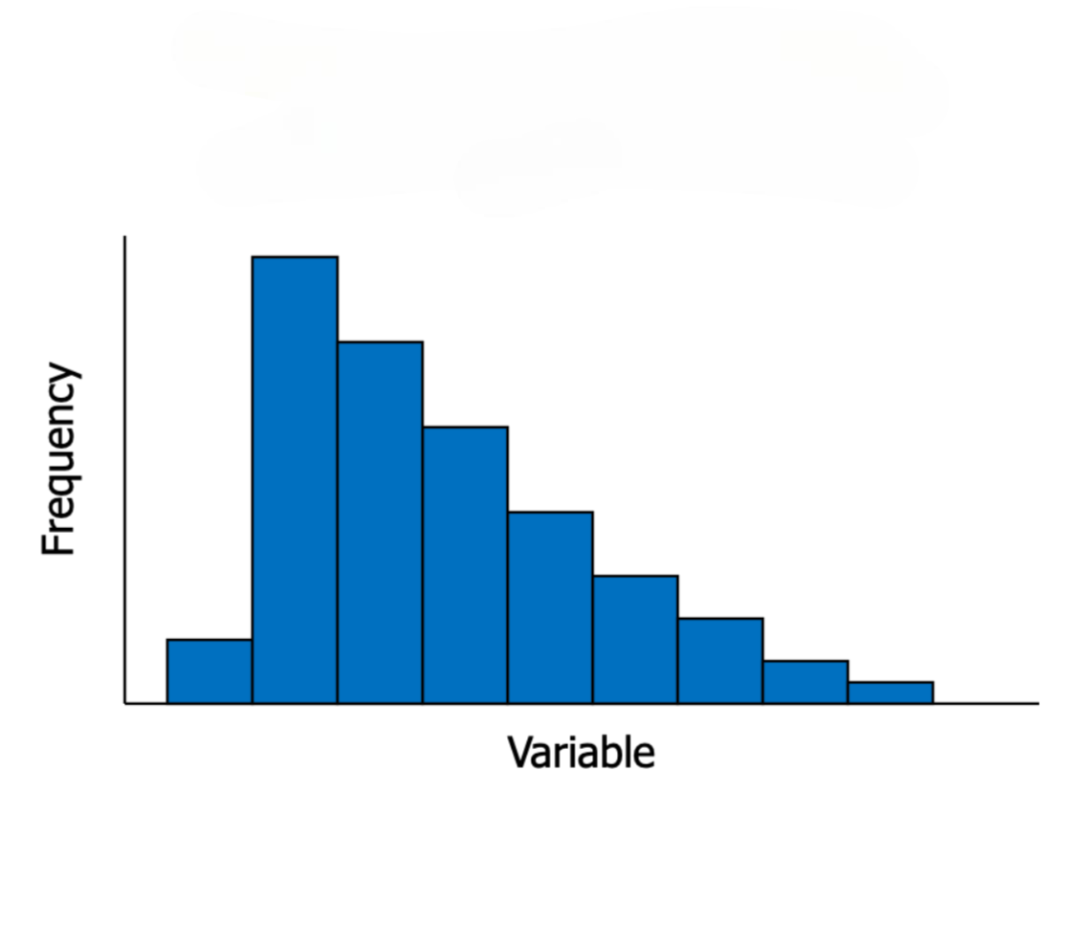
How would you describe the shape of the distribution in the provided image?

skewed to the right (positively skewed)

Looking at any data set provided on a graph (in general) , what would be considered an “outlier”?

Any data that lie far off the main body of the distribution

True or False.

Extreme values are known as “outliers”.

True.

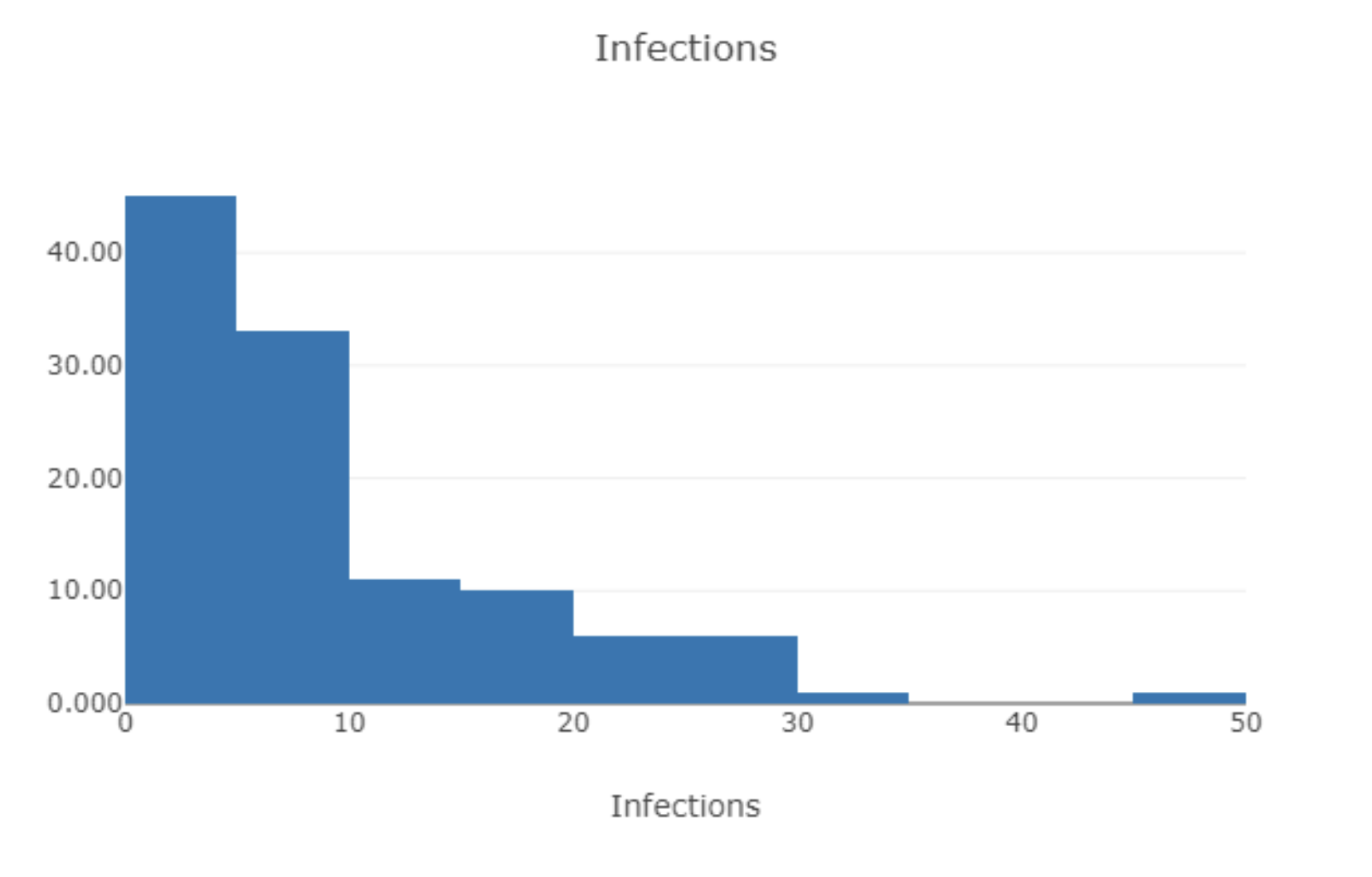
How would you describe the shape of the distribution of the variable, infections?

unimodel, skewed to the right & one outlier present

What are 2 different types of centres that an describe the pattern of distribution?

mean and median

What value is considered to be the “mean”?

A value that is the sum of all values of the quantitative variable divided by the number of values

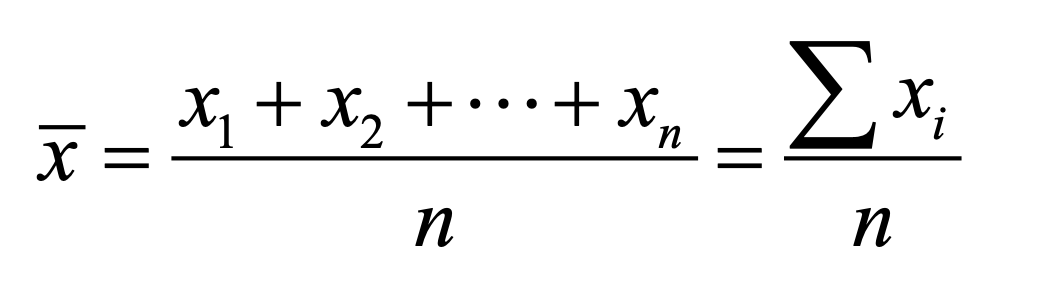
What is this formula (seen in the image) calculating for?

the mean

Fill in the blanks.

Mean is “_______” of data

center of gravity

True or false.

Mean is not sensitive to outliers.

False.

What value is considered to be the “median”?

A value that is the midpoint of all values, after they are
ordered from the smallest to the largest.

True or false.

Median is considered to be the value expressing 50% of values above & 50% below the median.

True.

For an even (#) number data set, how would you calculate the median?

You would take the mean of the two middle numbers.

True or false.

Median is robust to outliers.

True.

What does the term ‘robust’ mean?

less influenced by

Fill in the blanks. 

For symmetric distributions: mean __ median

For skewed distributions: mean __ median

For symmetric distributions: mean = median
For skewed distributions: mean >< median

Fill in the blank

When does a graph become left-skewed:

when mean __ median.

mean < median

Fill in the blank

When does a graph become right skewed:

when mean __ median.

mean > median

Answer the following questions on the provided image.

1. Median 

2. T

3. F

What are the 4 different types of spreads of distributions to consider when describing the pattern of distribution of a graph/chart?

range, standard deviation, IQR, variance

What does spread describe?

how much data vary about their centre

What is the formula used to calacuate the range of a data set?

range = max - min

True or false.

Range is not very sensitive to outliers.

False.

If your data set clearly has outliers present and you want to figure out a good measure of spread distribution for that particular data set provided. What spread of measure would you use?

IQR (interquartile range)

Fill in the blanks.

Quartiles are ___ values that divide distribution
into ____ parts, each containing ¼ of data.

3, 4

Fill in the blanks.
1st quartile (Q1) has __ of data below & __ above

¼ , ¾

Fill in the blanks.
2nd quartile (Q2) has __ of data below & __ above

½, ½

Fill in the blanks.

3 rd quartile (Q3) has __ of data below & __ above.

¾, ¼

Given a data set, how would you find Q1, Q2 and Q3?

Split the data into two halves, and the middle value would be the Q2. The first half of the data's middle value would be the Q1, and the second half's middle value would be the Q3. *NOTE: (if two values are present, take the mean of both values to obtain one value)

What is the formula to caluclate the IQR?

IQR = Q3 - Q1

What does IQR (interquartile range) mean?

It’s the distance between Q1 and Q3

Fill in the blanks.

IQR is _________ to outliers.

resistant

What measure is variance (s²)?

A measure that measures the average squared deviation of individual data from their mean.

What measure of units is variance always?

squared units

How would you calculate standard deviation?

s = √s² = √variance

What do both variance and standard deviation both measure?

the spread around the mean (distance)

Are variance and standard deviation both sensitive to outliers? Explain.

Yes, as they look at the measure from each data point to the sample mean (which, is sensitive to outliers)

What do both variance and standard deviation work best for?

symmetric distribution

What kind of measure is standard deviation?

measure of the amount of variation in a set of data 

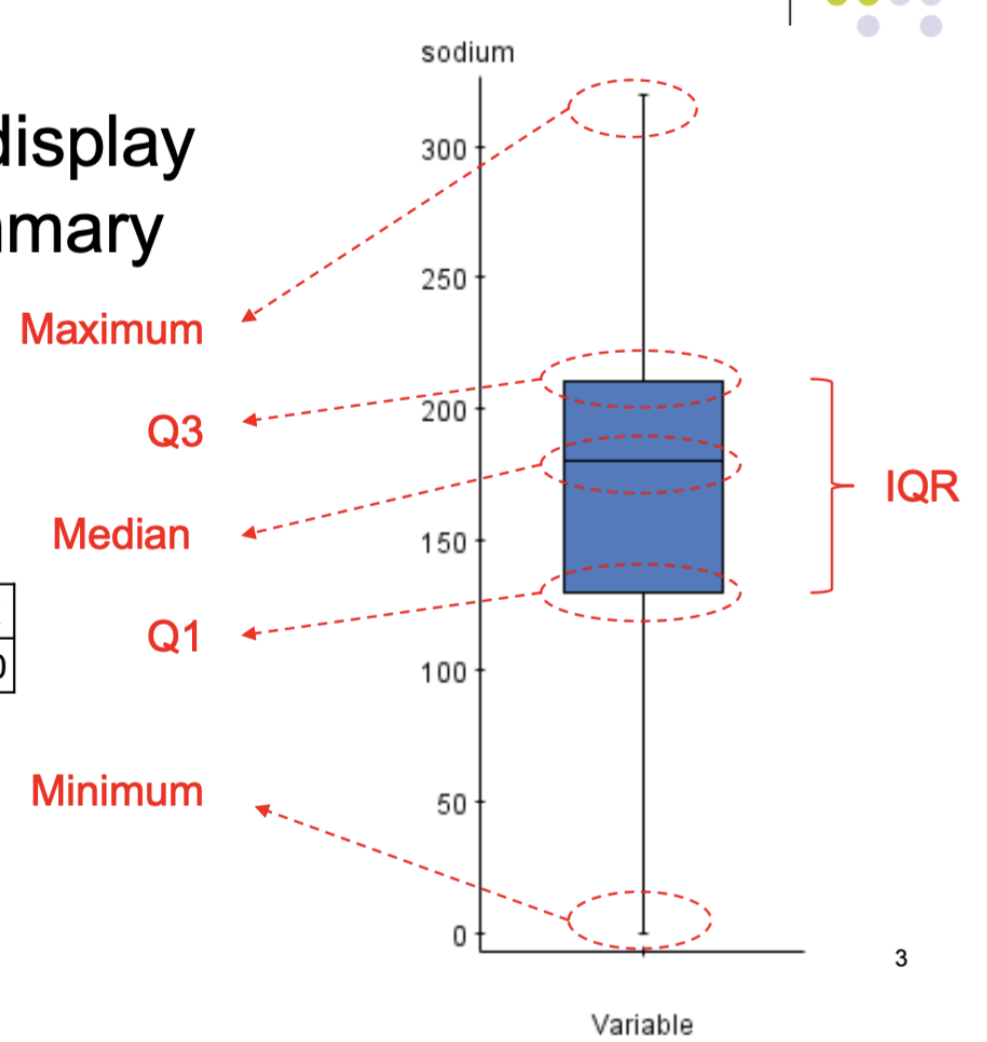
What is a 5-number summary?

A 5-number summary is set of five measures giving quick summary of a distribution.

What does the five-number summary consist of?

1. Minimum

2. Q1

3. Q2 - Median

4. Q3

5. Maximum

What would be a visual display of 5-number summary?

a boxplot

Why do boxplots aid in identifying outliers?

by calculating both the upper and lower fences, and drawing those fences on the boxplot - those points outside these fences are suspected the outliers

How would you calculate upper & lower fences?

upper fence = Q3 + 1.5 * IQR

lower fence = Q1 - 1.5 * IQR

Fill in the blanks.

Five-number summary is better for describing
__________________________.

skewed distributions w/ outliers

Fill in the blank.

___________ and __________ work well for reasonably symmetric distributions w/o outliers

mean, standard deviation

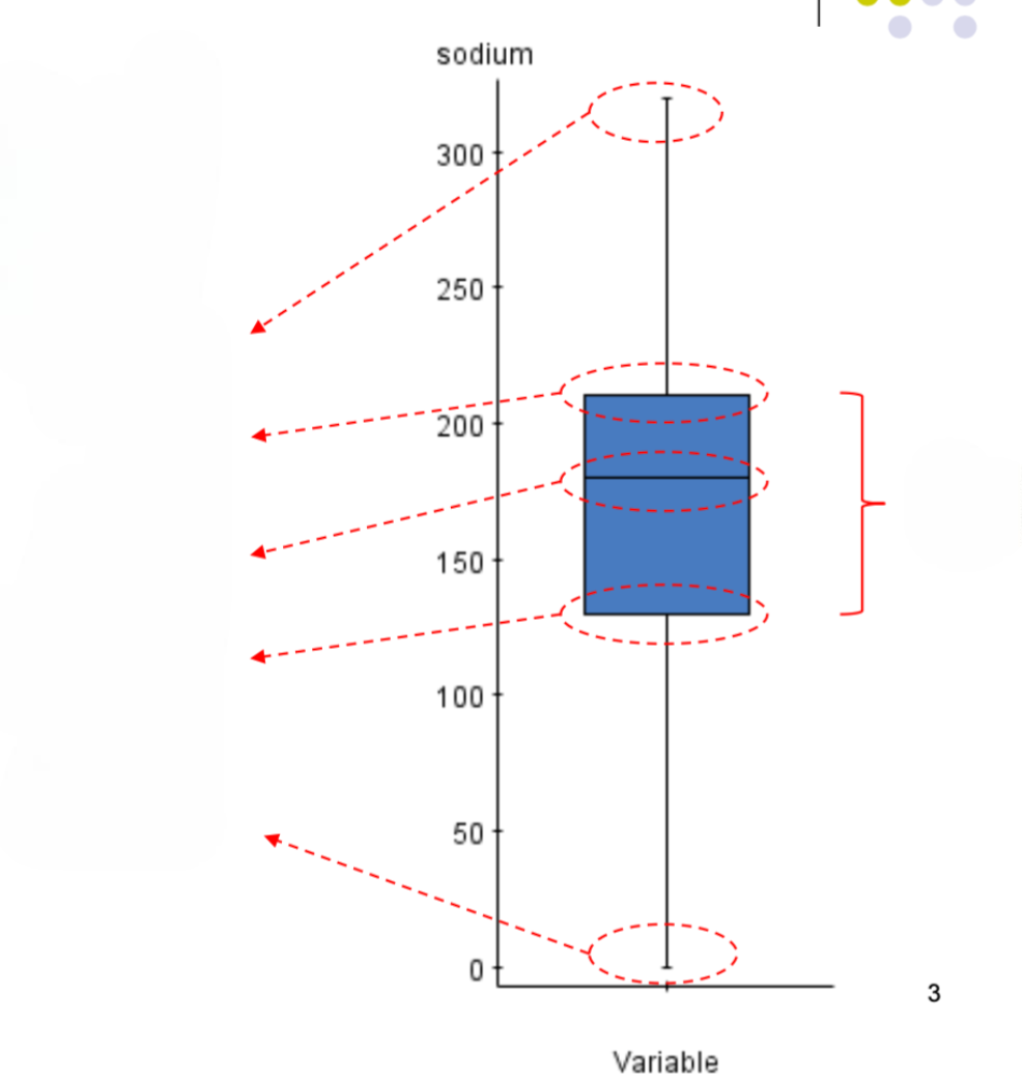
Fill in the blanks on this box-plot diagram?