Calc concepts

Define Integrals AKA Fundamental Thm of calc

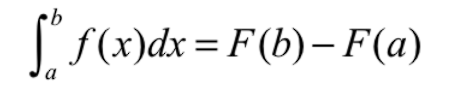
calc is the study of

change

derivatives oversimplified are

slope or rate of change

Integrals oversimplified are

area or total accumulation

Indefinite integrals AKA Antiderivative without bounds

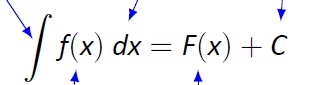
Mean value theorem AKA MVT

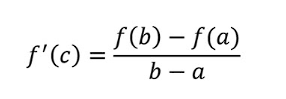
average y-value f(x) over [a,b]

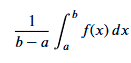
when a function equals its average y-value f(x) over [a,b]

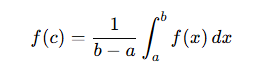
Total accumulation of f(t) over [a,b]

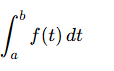
how negative area exists

right to left, under x-axis

Related Rates: Area of a Triangle with changing base and changing height

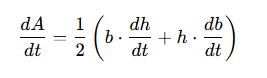
Related Rates: Area of a Triangle with constant base and changing height

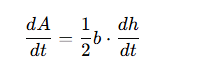
lim 1/x while approaching infinity

0

lim 1/x while approaching 0 from the positive side

positive infinity

lim 1/x while approaching 0 from both sides

does not exist

Left sided Reimann sum f(x) with 4 equal subdivisions LRAM4

f(x0​) = Y0 ect.

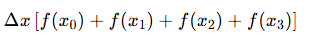
Right sided Reimann sum f(x) with 4 equal subdivisions RRAM4

f(x0​) = Y0 ect.

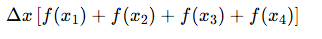
Local Maximum @ x= a by using only the 1st derivative test

f’(a) = 0/und , deriv goes (+) to (-)

Local Maximum @ x= a by using the 2nd derivative test

f’(a) = 0+ f’’(a) is (-)

point of inflection on f(x)

f’(x)=0 , f’’(x) changes sign f’’ = 0,und

one way to find a solution to an Initial value Problem (IVP)

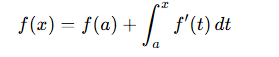
Tangent line to f(x) at x=a

f(x) - f(a) = f’(a)(x-a)

quotient rule

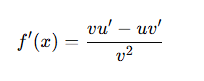
product rule

(f(x))(g(x)) = f’(x)g(x) +f(x)g’(x)

Chain rule of derivatives

f(g(x)) = f’(g(x))g’(x)