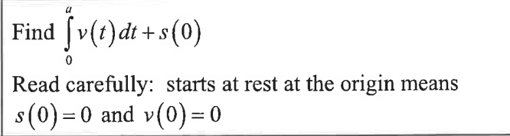AP Calc Exam Review

AP Wording Review Translating the AP Calc test when you see the words ... this is what you should think to do

find the zeros

find roots

set function = 0, factor or use quadratic equation if quadratic, graph to find zeros on calculator

show that f(x) is even

shoe that f(-x)=f(x)

symmetric to the y-axis`

show that f(x) is odd

shoe that f(-x)=-f(x) OR f(x)=-f(-x)

symmetric around the origin

show that limf(x) exists

show that LIM x—>a- = LIM x—>a+, exists and are equal

find lim f(x), calc allowed

use TABLE [ASK]

find y values for x-values close to A from left and right

find lim f(x), no calc

substitute x = a

1) limit is value if b/c including 0/c=0

2) DNE for b/0

3) 0/0 DO MORE WORK

a) rationalize radicals

b) simplify complex fractions

c) factor/reduce

d) known trig limits

find lim x—> infinity, calc allowed

use TABLE [ASK]

find y values for large values of x

i.e. 9999999999

find lim x—> infinity, no calc

ratios of rates of changes

1) fast / slow = DNE

2) slow / fast = 0

3) same / same = ratio of coefficients

find the horizontal asymptotes of f(x)

find lim —> infinity and lim —> negative infinity

find vertical asymptotes of f(x)

find where lim —> a pos or neg = pos or neg infinity

1) factor/reduce f(x) and set denominator = 0

2) lax has V at x=0

find domain of f(x)

assume domain is (negative infinity, pos infinity)

retractable domains:

• denominators don’t equal 0

• square roots of only non-negative numbers

• log or ln of only positive numbers

• real-world constraints

show that f(x) is continuous

show that

1) limf(x) exists (limx—> a from right = lim x—> a from left)

2) f(a) exists

3) lim f(x)= f(a)

find the slope of the tangent line to f(x) at x=a

find derivative f’(a)=m

find equation of the line tangent to f(x) at (a,b)

f’(a)=m and use y-b=m(x-a)

find equation of the line normal to f(x) at (a,b)

same as above but

m = ( -1 / f’(a) )

find the average rate of change of f(x) on [a,b]

find f(b)-f(a) / b-a

show that there exists a c in [a,b] such that f©=n

IVT

confirm that f(x) is continuous on [a,b]

then show that f(a) <(or equal to) n <(or equal to) f(b)

find the interval where f(x) is increading

find f’(x)

set both numerator and denominator to zero to find critical points

make sign chart of f’(x) and determine where f’(x) is positive

find interval where the SLOPE of f(x) is increasing

find the derivate of f’(x) = f’’(x)

set both numerator and denominator to zero to find critical points

make sign chart of f’’(x) and determine where it is positive

find instantaneous rate of change of f(x) at a

find f’(a)

given s(t) [position function], find v(t)

v(t) = s’(t)

find f’(x) by the limit definition

frequently asked backwards

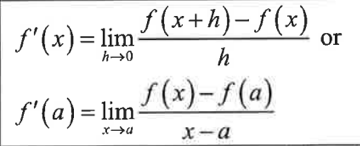
find the average velocity of a particle on [a,b]

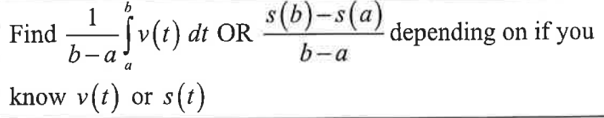
given v(t), determine if a particle is speeding up at t=k

find v(k) and a(k)

signs match = particle is speeding up

different signs = particle is slowing down

given a graph of f’(x), find where f(x) is increasing

determine where f’(x) is positive

(above the x-axis)

given a table of x and f(x) on selected values between a and b, estimate f’(c_ where c is between a and b

straddle c, using a value k (greater than c) and a value h (less than c)

so f’( c)= f(k)-f(h) / (k-h)

given a graph of f’(x), find where f(x) has a relative max

identify where f’(x)=0, crosses the x-axis from above to below

OR
where f’(x) is discontinuous and jumps from above to below the x-axis

given a graph of f’(x), find where f(x) is concave down

identify where f’(x) is decreasing

given a graph of f’(x), find where f(x) has pois

identify wehre f’x) changes from increasing to decreasing or vice versa

show that a piecewise function is differentiable at the point a where the function rule splits

first, be sure that the function is continuous at x=a by exaluating each function at x=a

then take the derivative of each piece and show that limx—> a from the right of f’(x) = limx—> a from the left f’x)

given a graph of f(x) and h(x)=f^-1(x) find h’(a)

find the point where a is the y-value on f(x), sketch a tangent line and estimate f’(b) at the point

then h’(a)= 1/f’(b)

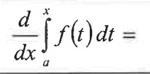
f(x)

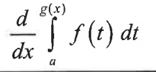
f(g(x))g’(x)

find area using left Riemann sums

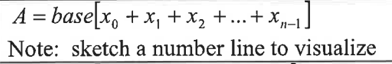
find area using right Riemann sums

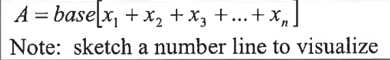
find area using midpoint rectangles

typically done with a table of values

be sure to use only values you are given

if you are given 6 sets of points, you can only do 3 midpoint rectangles

find area using trapezoids

describe how you can tell if rectangle/trapezoid approximations over or underestimate

overestimate: LH for decreasing, RH for increasing, trapezoids for concave up

underestimate: LH for increasing, RH for decreasing, trapezoids for concave down

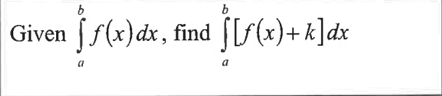
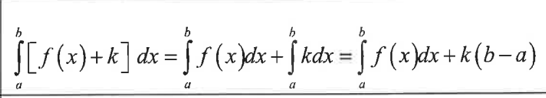
given dy/dx draw a slopefield

use the points given and plug them into dy/dx

draw little lines with indicated slopes at the poitns

y is increasing proportionally to y

dy/dx=ky translating to y=Ae^kt

solve the differential equation

separate the variables, -x on one side, y on the other

the dy and dx must all be upstairs

integrate each side, add C to x side

find C before solving for y (unless lny)

when solving for y, choose + or -, solution will be a continuous function passing through the initial value

find the volume given a base bounded by f(x) and g(x) with f(x) > g(x) and cross sections perpendicular to the x-axis are squares

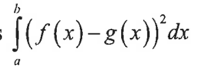
given the values of F(a) and F’(x)=f(x), find F(b)

usually this problems contains an antiderivative you cannot do

utilize the fact that if F(x) is the antiderivative of f, then integral from b to a f(x)dx= F(b)-F(a)

so solve for F(b) using the calculator to find the definitive integral

F(b)=integral from b to a f(x)dx + F(a)

meaning of integral from a to b of f(t)

the accumulation function: net (total if f(x) is positive) amount of y-units for the function f(x) beginning at x=a and ending at x=b

given v(t) and s(0) find the greatest distance from the origin of a particle of [a,b]

sove v(t)=0

then integrate v(t) adding s(0) to s(t)

finally compare s(each candidate) and s(each endpoint)

choose greatest distance (it might be negative!)

given a water tank with g gallons initially being filled at the rate of F(t) gallons/min and emptied at the rate of E(t) gallons/min on [0,b]

a. the amount of water in the tank at m minutes

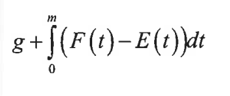
given a water tank with g gallons initially being filled at the rate of F(t) gallons/min and emptied at the rate of E(t) gallons/min on [0,b]

b. the rate the water amount is changing at m

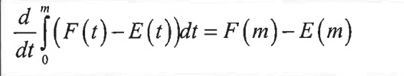
given a water tank with g gallons initially being filled at the rate of F(t) gallons/min and emptied at the rate of E(t) gallons/min on [0,b]

c. the time when the water is at a minimum

solve F(t)-E(t)=0 to find candidates, evaluate candidates and endpoints as x=a in *forumla

choose the minimum value

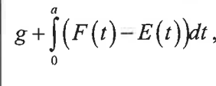
find the area between f(x) and g(x) with f(x)>g(x) on [a,b]

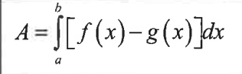
find the volume of the area between f(x) and g(x) with f(x)>g(x) rotated about the x-axis

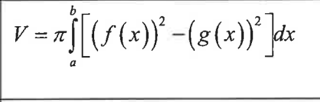
given v(t) and s(0) find s(t)

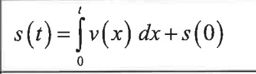
find the line x=c that divides the area under f(x) on [a,b] to two equal areas

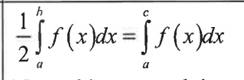
find the volume given a base bounded by f(x) and g(x) with f(x)>g(x) and cross sections perpendicular the x-axis are semi-circles

the distance between the curves is the diameter of your circle

so the volume is…

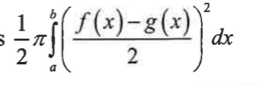
given the equation for f(x) and h(x)=inverse of f(x), find h’a)

understand that the point (a,b) is on h(x) so the point (b,a) is on f(x)

so find where f(b)=a

h’(a)= 1/f’(b)

given the equation for f(x), find its derivative algebraically

1) know product/quotient/chain rules

2) know derivatives of basic functions

• power rule

• e^x, b^x

• lnx, logx

• sinx, cosx, tanx

• arcsinx, arccosx, arctanx

given a relation of x and y, find dy/dx

implicit differentiation

find the derivative of each term, using product/quotient/chain rule appropriately, especially chain rule!!

every derivative of y is multiplied by y’

then group all y’ terms on one side, factor of y’ and solve

find the derivative of f(g(x))

chain rule

f’(g(x))•g’(x)

find the minimum value of a function on [a,b]

solve f’(x)=0

make a sign chart

find sign changes form neg to pos for relative minimums and evaluate those candidates along with endpoints back into f(x) and choose the smallest

find the minimum slops of a function on [a,b]

solve f’’(x)=0

make a sign chart

find sign changes form neg to pos for relative minimums and evaluate those candidates along with endpoints back into f’(x) and choose the smallest

find critical values

express f’(x) as a fraction if necessary

solve both numerator and denominator each equal to zero

find the absolute max of f(x)

solve f’(x)=0

make a sign chart

find sign change form positive to negative for relative maximums

and evaluate those candidates into f(x)

show that there exists a c in [a,b] such that f’©=0

MVT

confirm that f is continuous and differentiable on the interval

find k and j in [a,b] such that m = f(k)-f(j) / (k-j)

find the range of f(x) on [a,b]

use max/min techniques to find values at relative max/mins

also compare f(a) and f(b) (endpoints)

find range of f(x) on (-∞,∞)

use mas/min techniques to find values at relative max/minsalso compare limits to negative and positive infinity of f(x)

find locations of relative extreme of f(x) given both f’(x) and f’’(x)

(particularly useful for relations of x and y when finding a change in sign would be difficult)

Second Derivative Test

find where f’(x)=0, then check the value of f’’(x) there

if f’’(x) is positive —> f(x) has relative max

if f’’(x) is negative, f(x) has a relative min

find infection points

express f’’(x) as a fraction if necessary and set both numerator and denominator equal to zero

make sign chart of f’’(x) to find where f’’(x) changes sign

show that the line y=mx+b is tangent to f(x) at (x1,y1)

two relationships are required

same slope and point of interesection

check that m=f’(x1) and the (x1,y1) is on both the f(x) and tangent line

find any horizontal tangent lines to f(x) or a relation of x and y

write dy/dx as a fraction, set the numerator equal to zero

equation of tangent line is y=b

find nay vertical tangent line(s) to f(x) or a relation of x and y

write dy/dx as a fraction

set the denominator equal to zero

equation of tangent line is x=a

approximate the value of f(0.1) by using the tangent line to f at x=0

Linearization

y= f(a) + f’(a)(x-a)

find rates of change for volume problems

write the volume forumla

find V’

be careful about product/chain rules

watch positve (increasing measure) / negative (decreasing measure) signs for rates

find rates of change for Pythagorean theorem problems

x²+y²=z²

2xx’+2yy’=2zz’ (can reduce 2s)

watch positve (increasing distance) / negative (decreasing distance) signs for rates

find the average value of f(x) on [a,b]

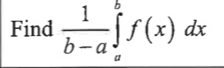
find the average rate of change of f(x) on [a,b']

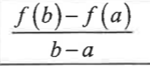
given v(t), find the total distance a particle travels on [a,b]

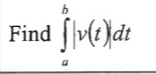
given v(t) find the change in position a particle travels on [a,b]

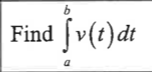
given v(t) and initial position of a particle, find the position at t=a