Fundamentals of data representation

number systems, number bases, units of information, binary number system, information coding systems, representing sound/ images

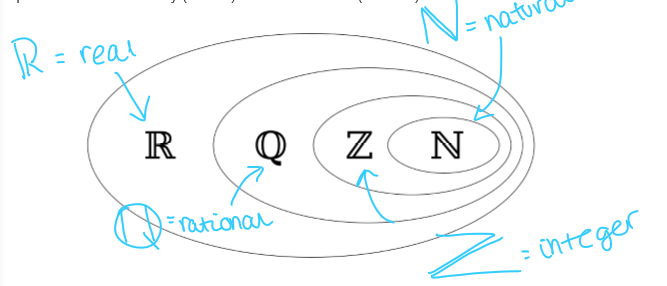
state the base number for denary, binary and hexadecimal

denary = base 10

binary = base 2

hexadecimal = 16

what is a natural number?

positive whole number, including 0

draw the symbol for a natural number

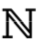
give an example for when natural numbers are used

• counting (e.g. “there are 6 people here”)

• ordering (e.g. “this is the 3rd largest city in the world”)

what is an integer number

whole positive OR negative number, including 0

draw the symbol for an integer number

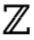
what is a rational number

any number that can be expressed as a quotient, fraction or ration

draw the symbol for a rational number

what is an irrational number

number that cannot be represented as fraction or ration since the decimal form will contain infinite repeating values

give 2 examples of irrational numbers

• pi

• square root of 2

what is a real number

any positive OR negative number with OR without fractional part

draw the symbol for a real number

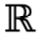
draw all the symbols for the number systems

what is an ordinal number

number used to identify position relative to other numbers

ordinal = ORDER

e.g. first, second, third

what is a cardinal number

identifies size of something

e.g. number of elements in array or characters in string, second out of 20

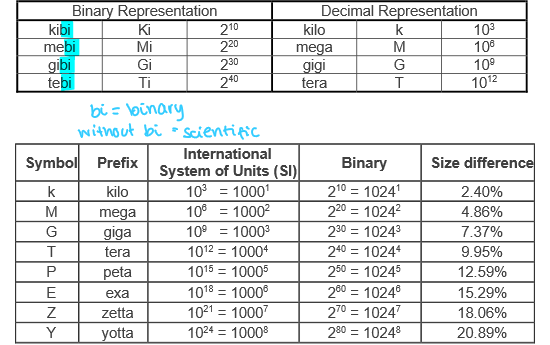
state the name of the units in binary. how do they differ from the scientific name

binary: x 1024

kibi, mebi, gibi, tebi

scientific: x 1000

kilo, mega, giga, tera, peta

what is the formula to figure out how many digits can be stored with a certain number of bits

n bits = 2ⁿ digits

what is the largest number that can be stored in an n bit word

2n - 1

PRACTICE:

how many bits would it take to store the number 125

125 log₂ = 6.96

…. therefore would need 7 bits

PRACTICE:

how many bits would it take to store the number 312

312 log₂ = 8.2

…. therefore would need 9 bits

convert the denary number 37 into binary

divide number by 2.

take note of the remainder.

repeat until remainder = 0

read from bottom up (i.e. the last remainder that is 0 takes the larges placeholder e.g. 128)

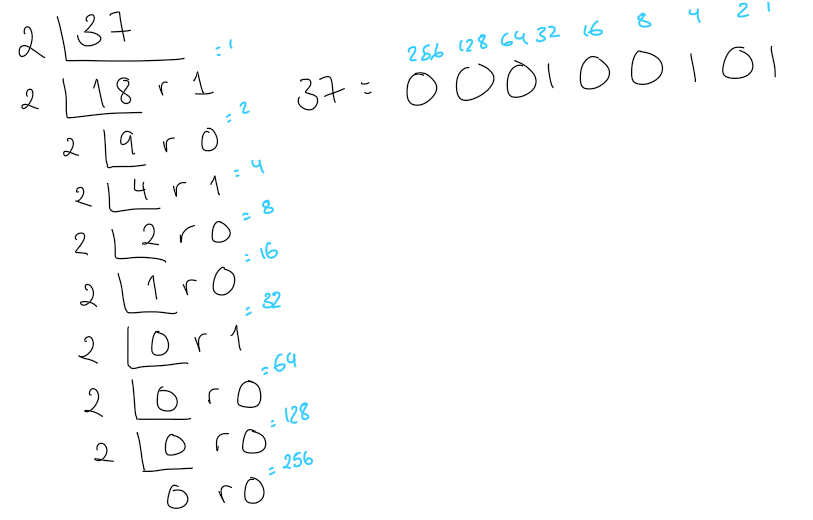
convert binary number 11001010 into denary

128 + 64 + 8 + 2 = 202

binary addition rules

0 + 0 = 0

0 + 1 = 1

1 + 1 = 0 carry 1

1 + 1 + 1 = 1 carry 1

how to multiply 2 binary numbers

multiply. then add.

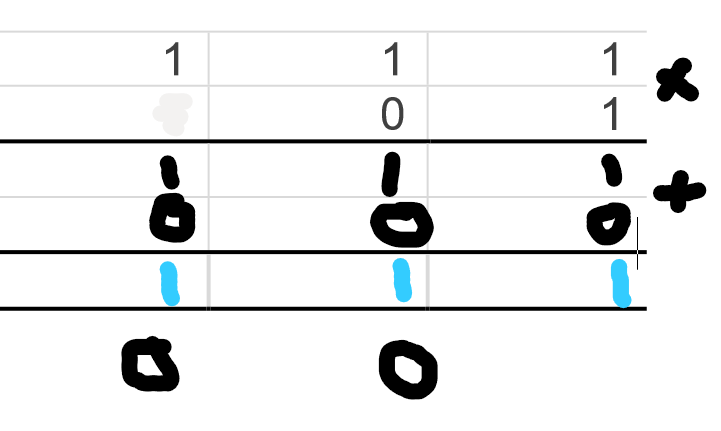
binary multiplication rules

0 × 1 = 1

1 × 1 = 1

how to represent unsigned and signed integers

if there is a 0 at the start = positive number

if there is a 1 at the start = negative number

rules for Two’s compliment

• start from least significant end, copy bits up to and including the first 1

• invert the remaining

how to convert -74 into Two’s compliment?

signed binary: -01001010

two’s compliment: 10110110

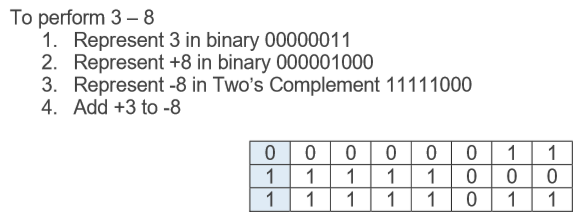
what is the method for subtracting binary numbers. use the example of 3 - 8

represent both numbers in binary

represent the second one in Two’s compliment

Add the first number to the negative second number

how to convert binary number into Hexadecimal

starting from least significant end, group binary number into blocks of 4

convert blocks into decimal

convert each decimal to hexadecimal

convert 0111111010₂ to hexadecimal

difference between fixed and floating point binary numbers

fixed: the decimal point is fixed so there is always the same number of integers before the decimal point and the same number of decimals places after the decimal point

floating: the decimal point is NOT fixed so it can be treated like standard form. uses a mantissa and exponent. have an exponent base of 2. mantissa is specified as point binary where binary point is placed in between most and least significant bit

evaluate using fixed point over floating point

• + makes arithmetic simple - therefore processing is faster

• - it is of limited range

evaluate using floating point over fixed point

• + range of numbers that can be represented with set number of bits is far larger

how are decimal numbers represented in binary?

convert +54.16 into fixed point binary

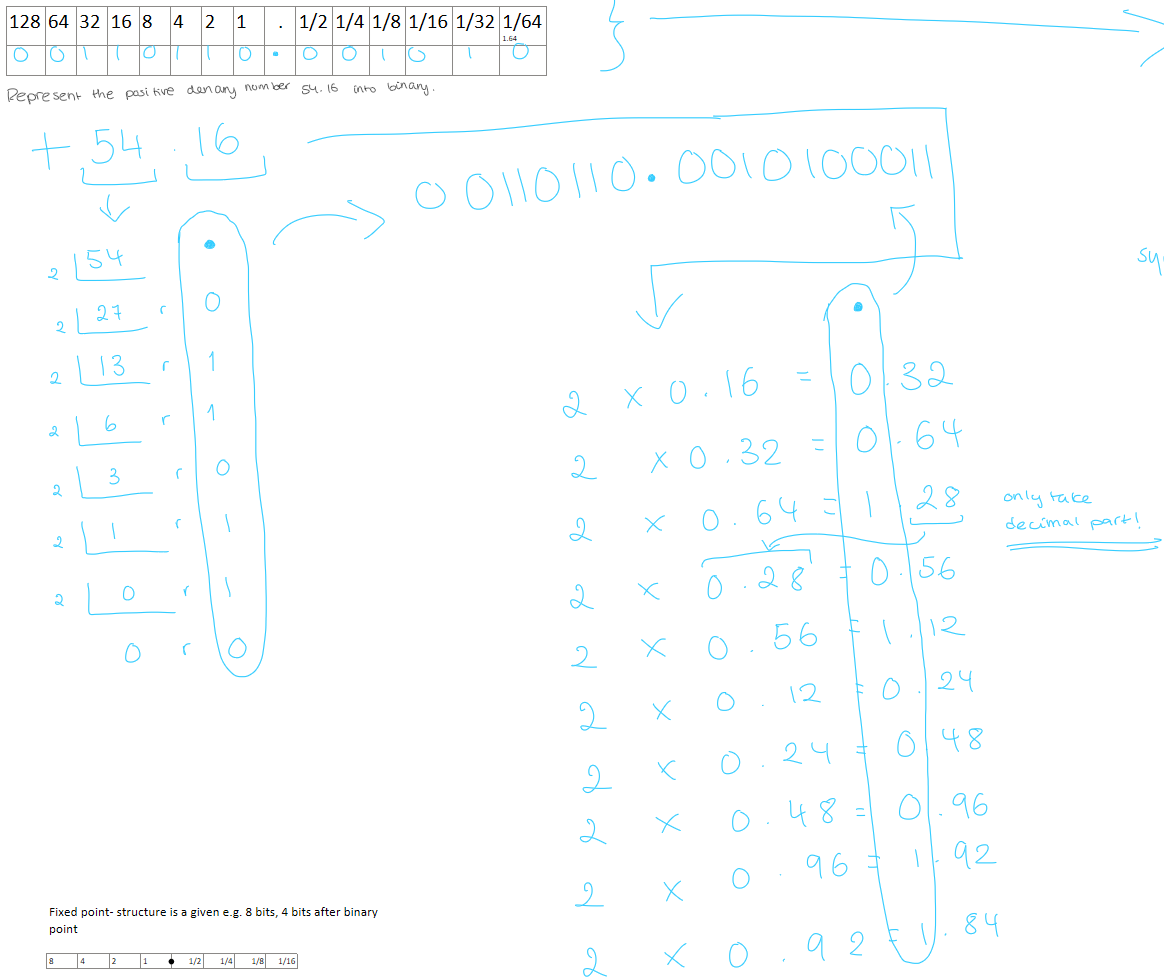
draw out the format for the mantissa and exponent:

effects of the size of the mantissa and exponent:

if the number of bits representing the mantissa is decreased and exponent s increased (keeping total number of bits the same) then:

• range of numbers that can be represented is increased (EXPONENT DEPENDENT)

• precision is decreased (MANTISSA DEPENDENT)

PREVIOUS EXAM QUESTION:

In an 8 bit mantissa, we can store 9 bits. How?

The first digit after the decimal point is the opposite of the first value because if it is a positive number, it will start 0.1 and if the number is negative, it starts with 1.0. Because of this, only the first value has to be stored and the one after can just be programmed to be the opposite. So, we can store an extra value in the 8 bit mantissa.

simplified method of normalising binary into floating point representation:

1. convert to binary

   1. method for whole number= keep dividing whole number by 2 and note the remainder. first remainder is least significant digit

   2. method for decimal part= times the decimal number by 2. every answer becomes the recurring number that is times by 2 (note: if answer = 1.55, times 2 by 0.55) until answer is 0.00. note the whole number of this process, the first digit calculated is the start of the decimal part

2. perform twos compliment if needed

   1. copy up to and including first 1

3. normalise

   1. if decimal point moves ← (left), exponent = positive

   2. if decimal point moves → (right), exponent = negative

4. convert exponent into binary

   1. perform twos compliment on exponent if negative (decimal moves backwards/ right .→)

5. write out answer in specified mantissa and exponent format

normalise the denary number 7.75 as the binary floating point number with an 8 bit mantissa and a 4 bit exponent

1. represent number in binary

   1. 00000111.1100

   2. method for whole number= keep dividing whole number by 2 and note the remainder. first remainder is least significant digit

   3. method for decimal part= times the decimal number by 2. every answer becomes the recurring number that is times by 2 (note: if answer = 1.55, times 2 by 0.55) until answer is 0.00. note the whole number of this process, the first digit calculated is the start of the decimal part

2. normalise

   1. 00.1111100

   2. move decimal place to LEFT(positive move) by 3

   3. needs to be +ve so has to start with 0.1

3. write move in standard form

   1. 00.1111100 × 2³

4. convert the exponent into binary

   1. 00.1111100 × 2⁰⁰¹¹

5. ANSWER:

normalise -7.25 in floating point binary with 8 bit mantissa & 4 bit exponent

1. convert to binary: -00111.0100

2. twos compliment: 11000.1100

3. normalise: 11.0001100 × 2³

4. simplify: 1.0001100 × 2⁰⁰¹¹

5. 8 bit mantissa & 4 bit exponent = 1.00011000011

give the largest/ smallest positive/ negative numbers represented in normalised floating point

Largest positive we can represent = 0111.1111 = 7

Largest negative we can represent = 1000.0000 = - 8

Smallest positive we can represent = 0000.0000 = 0

Smallest negative we can have = 1111.1111 = - 0.0001

Advantage of normalised floating point numbers

• gives unique representation of each number

• maximises precision for given number of bits

• increases range of numbers represented in given number of bits

• can test for equality easier e.g. 0.101011 0100 is same as 0.110011 0100

• uses standard form so can easily compare numbers based on exponent (which one is bigger/ smaller) - see example:

how to represent 9.125 and -1.25 in normalised floating point binary?

define precision

max number of significant digits that can be represented

(i.e. how close computer calculated value is compared to actual value)

fill in the gap:

the greater the mantissa, the more _________ we get

the greater the mantissa, the more precision we get

define rounding + give example of error

method used to change current number to new number which is closest to actual value

error = absolute error

define absolute error

difference between actual number and nearest representable number

fill in the gap:

an absolute error will always be _________

an absolute error will always be positive

How to calculate absolute error

calculated number - actual number

how to calculate relative errors

absolute error / actual number

define cancellation error:

when two floating point numbers are added or subtracted in a way that the result is unchanged from the larger of the two numbers

explanation of what a cancellation error is:

Close to the real magnitude of the number BUT we remove the last couple digit at the end of the number. Keeping the expenses of the lower significance end for the higher significance end. LOOSING LEAST SIGNIFICANT BIT of our number

how cancellation errors happen with example:

• two numbers of completely different magnitudes are subtracted

• two numbers of equal magnitudes are subtracted

how can cancellation errors be avoided?

rearranging the equation in such a way that small numbers are not subtracted

define overflow

result of numeric calculation becomes too large to be stored in space reserved for numbers

state situations where overflow occurs

• adding small number to very large number

• multiplying two very large numbers together

define underflow

result of numeric calculation is too small to be represented by computer

state situations where underflow occurs

• dividing small number by very large number

• multiplying two very small numbers together (e.g. 1/128 × 1/128 = 1/16384)

how many bits is ASCII code & what does it represent

• 8 bits with the 8th bit being a parity bit

• represent letters and symbols found on standard keyboard

why was extended ASCII created?

used all 8 bits (with no parity) so could increase number of characters represented to 2⁸ (256) different combinations

How are ASCII codes grouped together?

0 - 31 = Control/ non printable characters (e.g. TAB)

32 - 127 = printable characters (punctuation, letters, digits)

extended ASCII: 128 - 255 = additional printable characters

• every symbol has a unique binary code (even if it’s non printable)

how many bits does Unicode use & what additional features did it add from ASCII?

16 bits to represent each character

can store 2¹⁶ (65536) characters

plane (page) 0 contain basic character sets, the 17 other pages are used for multilingual ideographics (e.g. emojis & heiroglyphics)

backward compatible with ASCII

What is UTF-8?

• unicode transformation format

• variable width character encoding system

• capable of encoding all valid character codes in unicode using for 8-bit bytes

• backwards compatible with ASCII

How does UTF-8 work?

• first 128 characters correspond one-to-one with pure ASCII so can use 1 single byte

• next 1920 characters need 2 bytes to cover almost all alphabets (e.g. Latin, Greek, Cyrillic)

• 3 bytes needed for characters in rest of basic multilingual plane (e.g. Japanese, Korean)

• 4 bytes needed for characters in other planes of Unicode (e.g. emjois, maths symbols)

outline RLE for text

• run length encoding

• form of lossless compression where aim is to reduce number of bits to represent set of data so text will take up less storage space & be quicker to transfer

• runs through text & counts number of consecutive occurrences of each character

complete the run length encoding for this set of data:

negative compression

text with few repetitions will not compress well - compressed version uses more storage space than uncompressed version

possible solution to negative compression

use a special byte value which flags when run will occur. BUT, this does mean any run of bytes automatically has additional byte added to it

e.g.

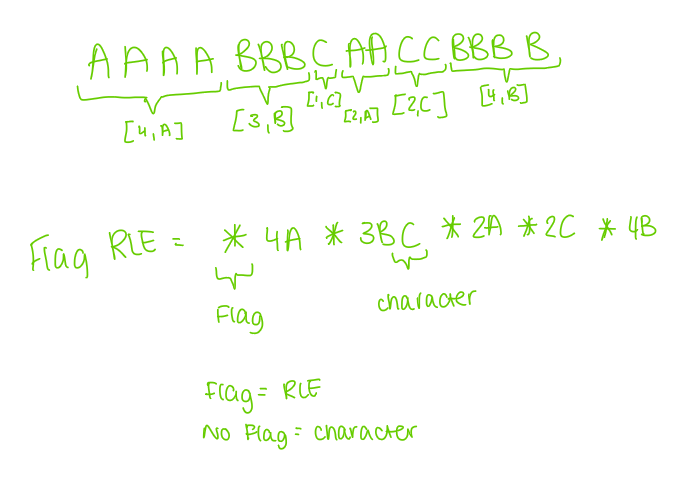
define bit-map images

images created when pixel of image are mapped to positions in memory that store binary codes representing colour of each pixel

define pixel

smallest addressable area of colour in image

define metadata and give examples for an image

• data about the data

  e.g. height, width, no. of colours, date, time, location

define resolution

number of pixels which appear per inch/ cm of image

higher the resolution…

• better quality of image

• closer can zoom without image becoming pixilated/ distorted

define colour depth

number of bits being used to store value/ colour of each pixel

the greater the size

higher the colour depth…

the greater the variety of colours available to be used

the greater the size

work out number of bits to store 256 colours = log2(256) = 8 bits

calculation for file size of bitmap image:

resolution x colour depth

• calculates it in BITS

what are vector graphic images

images made up of objects & coordinates

how do bit-map and vector graphic images DIFFER?

bit-map: holds info on value of each individual PIXEL (e.g. colour depth)

vector graphic: holds details of lines & shapes that make up image (e.g. squares, circles)

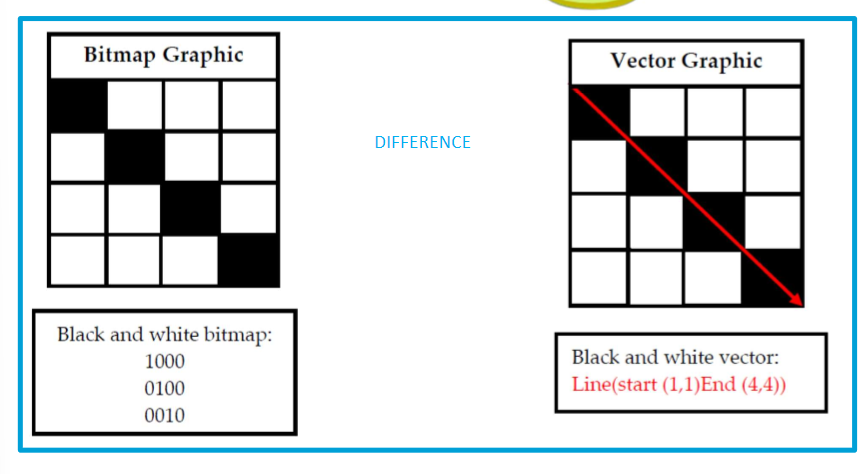
How are vector graphic images stored?

start and end coordinates of line are stored and computer interprets them as a line of given colour and width between these points

each pixel on output device is turned on when line crosses it to create visual image

advantage of vector graphics over bit-map images

• they are scalable

  • vector graphics simply scale coordinates and shapes so individual pixels on output device are not affected

• if you increase size of bitmap image, size of individual pixels must increase leading to pixilation

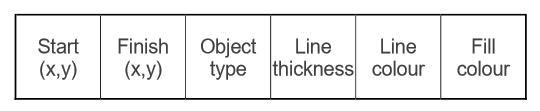
EXAM Q: write out the supposed data structure of storing info about vector object

• can be a stack to produce layers which can move back and forth

comparing bitmap vs vector graphic images:

state the 2 compression techniques and how they reduce file size

• lossless

  • can convert original files into condensed form AND use the inverse algorithm to convert it back

  • no loss of data

• lossy

  • permanently removes data when compressing a file so original & decompressed files are not identical

state 2 methods of lossless compression

• run-length encoding

• dictionary- based encoding

how does run-length encoding operate with images?

• eliminates repeating data

• if 3 or more consecutive pixels contain same bit pattern, a ‘run of cells’ has been found that can be encoded into 2 bytes

  • first byte = run/ number of identical consecutive memory cell bytes

  • second byte= colour of run

how does dictionary-based encoding work?

• within data, there are common repeating groups replaced with a token

• e.g. :

state a method of lossy compression

JPG

state ways in which we can represent sound:

-analogue signal (electrical signal that varies in continuous manner)

-digital data (data takes form of discrete values)

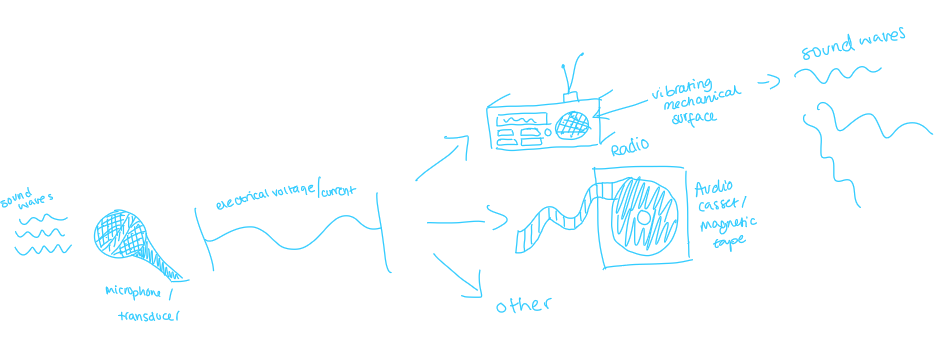
how is sound created and used in sound systems?

air pressure wave → sensed by ears → pressure wave captured by transducer (microphone) → produces electrical voltage/ current → transmitted through telephone/ broadcast through radio/ preserved on magnetic tape → electrical signal recreates sound by vibrating mechanical surface in loudspeaker → produces original pressure wave with varying degrees of fidelity → we hear this

how does a vinyl LP record exploit shape of sound?

• fixes similar shape in long spiral grove (stores data about sound in analogue form) on surface of record

• when record played, fine needle follows changes in groove & creates electrical signal proportional to changes

• then, signal is amplified & fed to loudspeaker

what is the purpose of a transducer? give examples

converts energy from one form to another

e.g. microphone: converts continuously varying sound pressure WAVES into continuously varying ELECTRICAL SIGNAL

e.g. loudspeaker: converts electrical energy to sound energy

the higher the pitch of the sound…

the more rapid/ frequent the vibration

the higher the loudness of sound…

the higher the amplitude of the soundwave

audio cd

define analogue quantities

physical quantities that vary continuously

e.g. temperature & pressure

define analogue data

data which varies in continuous manner

e.g. speech conveyed from speaker to listener by sound waves

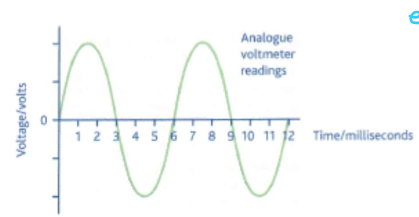
define digital data

discontinuous, varying data. discrete values

when analogue waves are sampled, they become digital