Crystallography & Diffraction - Exam 2

What does each reciprocal lattice point represent in real space?

A plane.

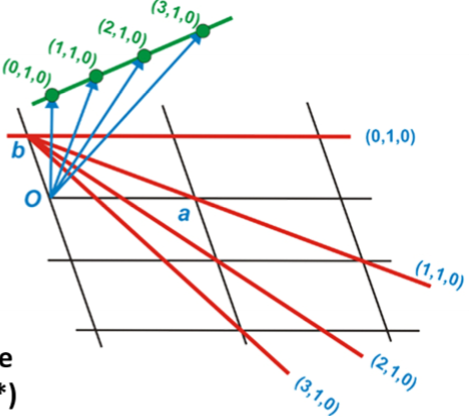
What are 2 main parameters that define a lattice plane (hkl)?

1. The orientation, given by the normal vector

2. The interplanar d-spacing of the plane.

What direction do lattice vectors occur and what are their magnitudes?

Occur in the direction of the plane normals.
Magnitudes are inverse to the planar spacing.

True/False? Diffraction occurs only in discrete directions corresponding to reciprocal lattice points.

True

What is Bragg’s Law

nλ = 2dsin(θ)

n = integer

d = periodic spacing

θ = angle of inclination from the periodic direction

What are scattering vectors s and s₀?

Represent the directions of the incoming and outgoing waves and have equal magnitudes of 1/λ

What are the steps for creating an Ewald Sphere?

1. Start with the reciprocal lattice of a crystal

2. Imagine a sphere with a radius equivalent of the incident wavelength^-1 and attach it to the origin

3. Rotate the sphere about the origin until it touches a reciprocal lattice point

4. Identify the incoming and outgoing wave vectors

5. Identify the scattering vector

6. This is a valid diffraction condition for the crystal

What will happen to the diffraction angles in an Ewald sphere if the wavelength is decreased?

s and s₀ are 1/λ so they get larger

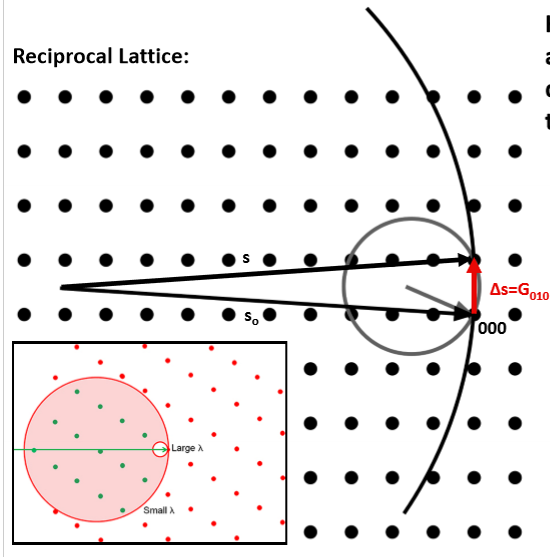
What 5 pieces of information do Ewald spheres on a reciprocal lattice give us?

1. Planar spacings

2. Planar orientations

3. Diffraction angles

4. Diffraction orientations

5. Physically possible peaks

What are the free variables in Bragg’s law?

Wavelength and Incident Angle

What is Laue Diffraction?

A technique that varies the wavelength by using a polychromatic “white” source at a fixed incident angle. It will capture a number of diffraction conditions with different planar spacings and orientations simultaneously.

Are the diffraction peaks observed in Laue Diffraction the normal vectors of the diffracting planes?

No - the normal vectors will bisect the angle between the incident and diffracted beams.

What is the precession method?

Involves tilting both the crystal and the detector at the same time, along with filtering out some of reciprocal space by only letting signal through an annulus (hole) in real space. This yields distortion free planar sections.

What is Euler’s Equation?

e^iθ = cosθ + i*sinθ

What is |x + iy|² = x² + y² in expanded form?

|x + iy|² = (x + iy)(x - iy)

What is the wave intensity?

The intensity of a wave function is the energy per area per time.

Intensity ∝ Amplitude²

What is wave polarization?

When all waves from a source share the same plane of vibration.

When waves are randomly oriented they are unpolarized.

What is the wave equation using Euler’s equation?

Wave = A₀e^{i(kx - ωt + φ)}

A₀ = amplitude

k = wave number (points in direction of propagation and has units of inverse length

ω = angular frequency

φ = phase shift

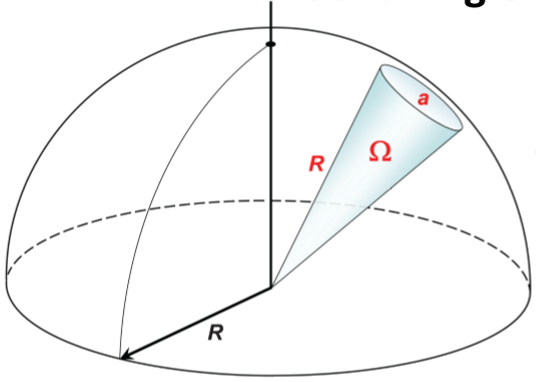
What is a solid angle?

The surface of a sphere covered by a swath of angular space (θ, φ), measured in “steraradians”

Ω = area/R²

dΩ = sinφ dφdθ

What will the intensity of diffraction be affected by?

The underlying crystal structure and microstructural and diffraction geometry considerations. The final intensity will be a function of many multiplicative factors.

Intensity ∝ F(Δk)²*S(Δk)²*M*L*…

What is the Huygens-Fresnel Principle?

Every point on a wavefront can be treated itself as the source of spherical wavelets. A planar wavefront will behave as if it is originating from a series of spherical wave sources located at an interface or aperture.

What will happen if a wavefront encounters a point object?

The incoming planar wavefront has an initial amplitude which will scale with the number of photos or particles it contains. Upon hitting the point object these particles will scatter and form a spherical wave front. The total number of particles is conserved, but as the wavefront is now expanding the amplitude is not.

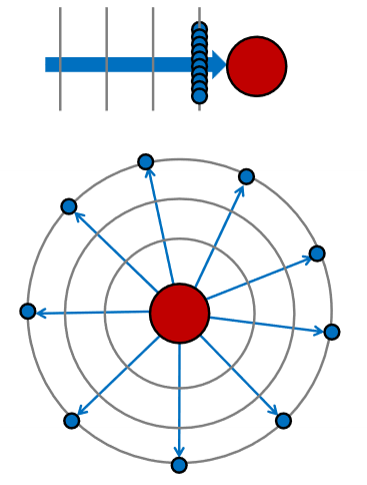
If the scattered intensity is uniform in all directions, how fast must the intensity of the wave fall in order to conserve energy?

Same energy is spread at each point over a sphere of area 4πR². The flux per are must fall by 1/R². ← Inverse square law

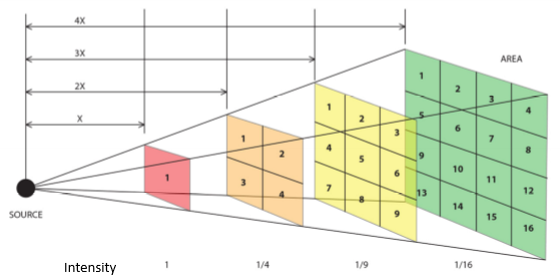
What is Thomson Scattering?

Radiation interacts with the field of the electrons and is re-emitted as a dipole source that has a strong polarization dependence.

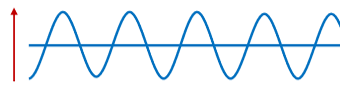
Imagine a polarized wave traveling through space as a physical object (a vibrating string). The amplitude is oscillating in a single plane, the plane of polarization, which must be orthogonal to the direction of travel.

How much of this vibration would transfer through to a second string if we attached the two together at a node?

The amount of the oscillation transferred will depend on the projection of the original amplitude to the direction orthogonal to the new travel direction.

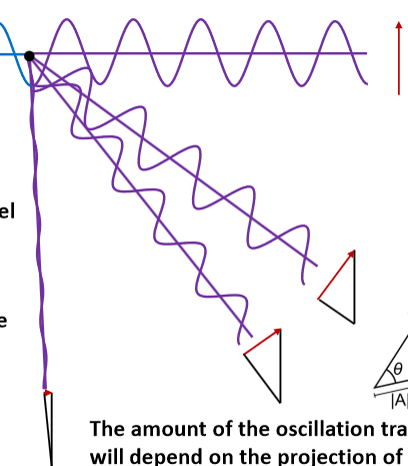
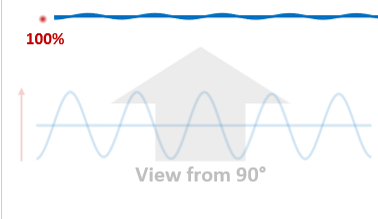
Imagine a polarized wave traveling through space as a physical object (a vibrating string). The amplitude is oscillating in a single plane, the plane of polarization, which must be orthogonal to the direction of travel.

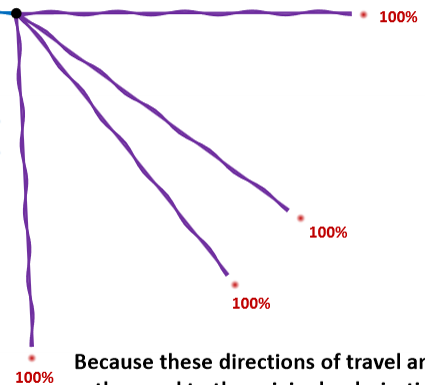
What if we are looking at the wave top down. Will the amplitude be affected if we try to transfer the oscillations in these directions?

Because these directions of travel are also orthogonal to the original polarizations, they have no issues transferring without loss.

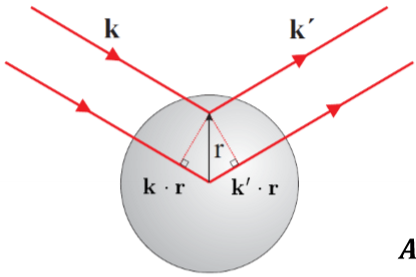
Describe the intensity of diffraction for an atom.

An atom has a finite size and features (electron cloud) that must be handled like a density function (of many infinitely small points). As the density function has a spread through space, this means that the waves emitting from different regions will have different phases and can interfere with each other.

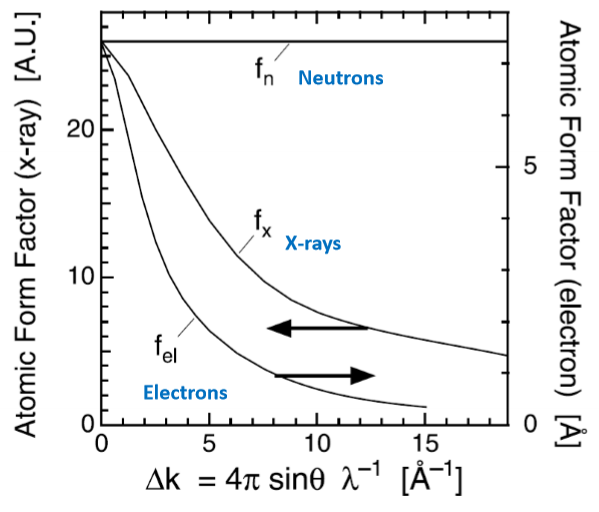
Describe the atomic scattering factor for X-rays.

For X-rays, the factor will use the electron cloud density as the density function.

f_X-ray = amplitude scattered by atom/amplitude scattered by a single electron

How will the structure factor change for an ionized atom?

The form for an ionized atom must meet up with the atomic number (Z) corresponding to its number of electrons (rather than protons), but will hybridize and resemble the non-ionized state at larger values (the radial density of the electron cloud is heavily influenced by the pull of the protons).

Describe the atomic scattering factor for electrons.

In electron scatting the electron wave interacts with the columbic potential of the atom rather than electron density function. Atomic scattering factor data for electron diffraction no longer comes to integer Z values when s = 0

The neutron scattering function for an atom is effectively independent of the angle. Why?

Neutrons don’t interact with electrons. The nucleus they interact with is a virtual point object, so there is no ability to develop a phase shift within the object.

Neutron cross-sections are based on complicated interactions with the nucleus, which means the scattering factors don’t follow a clear trend.

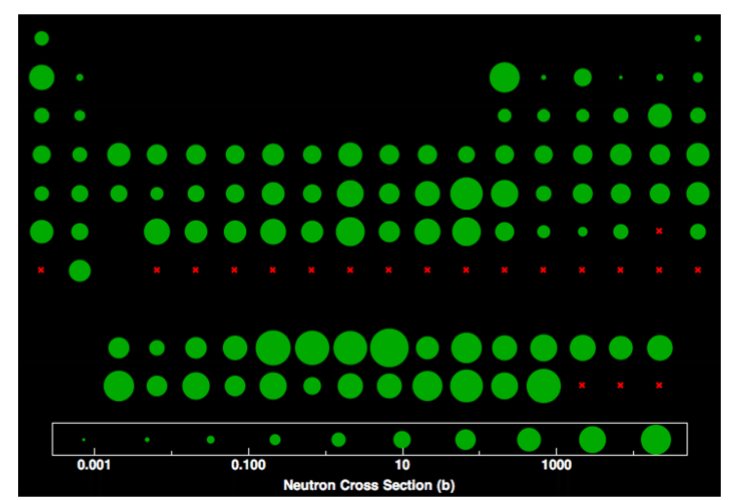
Describe the plot comparing the atomic scattering factors for neutrons, X-rays, and electrons.

What does e^nπi equal?

e^nπi = (-1)ⁿ

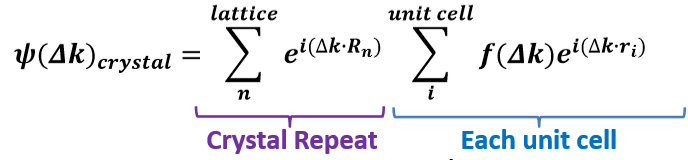
Describe the phase difference that results from scattering from multiple atoms.

The phase difference contributed by an ensemble of atoms can be treated like a summation as the integral over the atomic density function, the scattering factor f(Δk).

The vector location of any atom in a crystal can be reach by a combination of what 2 vectors?

Lattice and Basis

What is the shape factor dependent upon?

Shape and size of the crystallite.

What is the structure factor dependent upon?

Only on the crystal structure.

What is the equation for the structure factor?

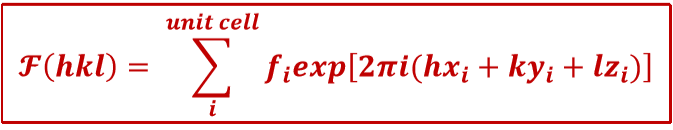
What does the lattice set? What does the basis modify? (sorry this is a badly worded question)

The lattice sets the allowed peaks, the basis modifies the intensity.

What are systematic absences?

Systematic absences of some diffraction conditions can arise from symmetry within the crystal structure, even if the cell is primitive in nature. All (hkl) conditions are possible for a primitive lattice but an added basis can negate them.

What does the shape factor tell us?

It tells us how the intensity of diffraction will scale with variations of the scattering vector due to crystal size.

Where does diffraction occur?

Near reciprocal lattice points (within some tolerance)

What will affect the shape of the diffraction intensity profile?

It will sharpen with a large number of lattice spacings (crystallite size) and broadens with a smaller number of lattice spacings. Integrated intensity scales by number of atoms.

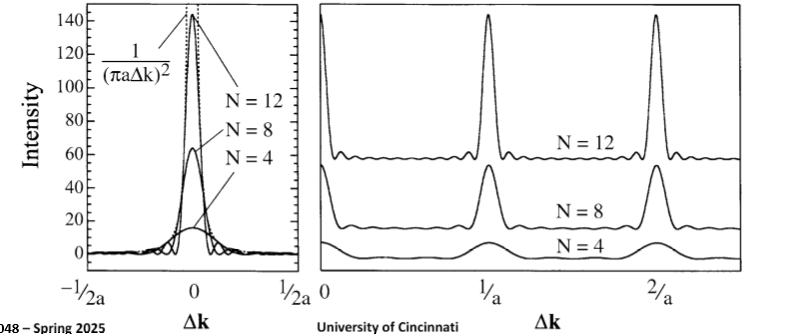
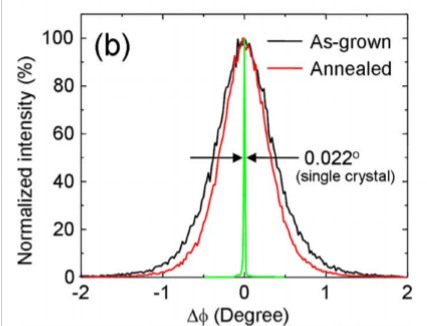
Comparing Bragg diffraction intensity of single crystalline vs polycrystalline samples, why are the polycrystalline peaks broader?

Small crystallites (grains) → shape factor

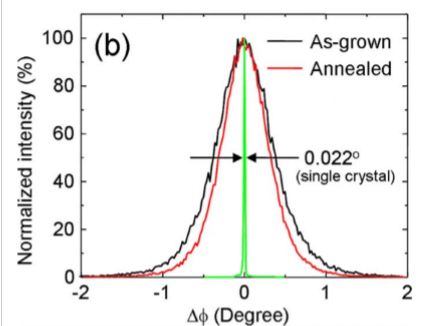
Why is the annealed condition becoming sharper?

Several possibilities, grain growth will increase the crystal size, but annealing will also remove some defects (dislocations) and makes the lattice parameter more uniform (less spread of diffraction d_hkl conditions)

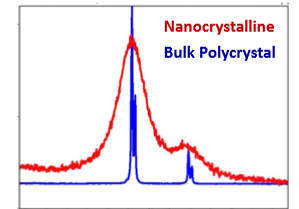
What happens to the Bragg diffraction peaks if we have very small crystals?

Peaks can get very broad, nanocrystals have a very large tolerance for non-perfect diffraction.

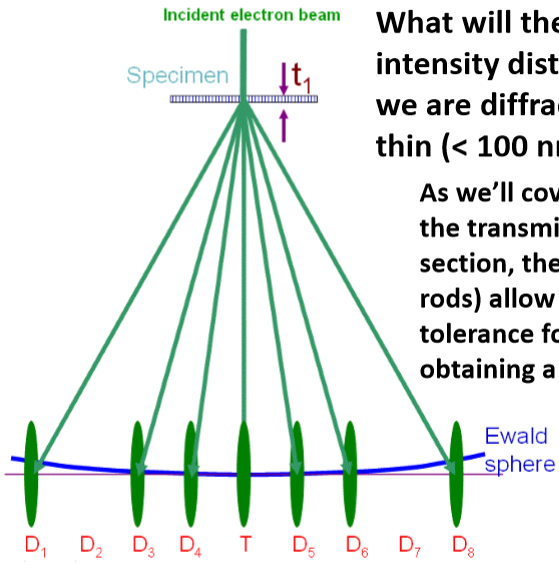
What will the reciprocal space intensity distributions look like if we are diffracting through a thin (<100nm) TEM sample?

For most materials, what is the shape of their intensity distribution function?

They are effectively sharp points located at reciprocal space lattice conditions.

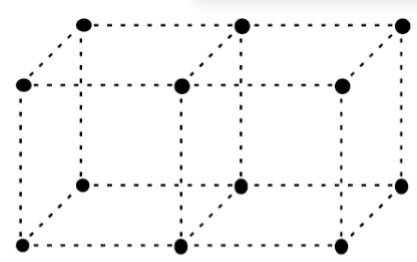
When diffracting crystals become small (<1μm), especially when they have a dimension smaller than 10nm, what is the shape of the intensity distribution function?

It starts to become more relevant and leads to significant amounts of diffraction away from the ideal.

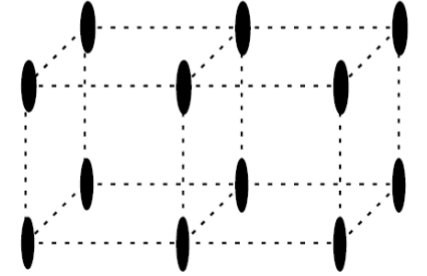
What will the reciprocal space condition of a mono-layer film or a 2D material such as graphene look like?

Effectively a forest of lines rather than points.