ANOVA

What is an ANOVA test

ANOVA = used for 3 or more groups/means 

Describe a one-way ANOVA

One-way ANOVA = Design indicates one independent variable/factor (“one way”) WITH three or more levels and 1 dependent variable 

• Determines if observed differences among a set of means are statistically significant from each other 

• Based on F-statistic, instead of t-value 

• Ex: A researcher is studying the effects of different assistive devices on stride length in a population of above-knee amputees. There are three groups: control (no assistive device), cane, and crutches 

  • Control vs Cane vs Crutches 

• Ex: measuring mean # of texts/month in three age groups 

CLASS:

3 samples looked at for 1 dependent variable

• 3 groups compared

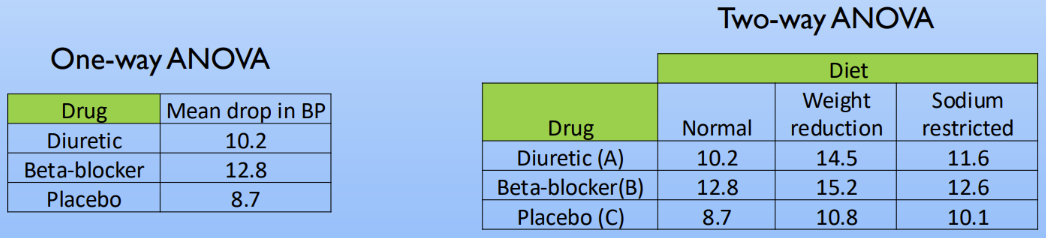
Describe a two-way ANOVA

Two-way ANOVA = Two independent variables/factors (each with 2 or more levels/categories) and one dependent variable 

• Looking for interactions between the independent variables 

  • One drug may be more effective when combined with a specific diet 

• Ask 3 questions: 

1. What is the effect of variable A, independent of variable B? (main effect) 

2. What is the effect of variable B, independent of variable A? (main effect) 

3. What is the joint effect of interactions of variables A and B? (interaction effect) 

• Ex: measure the effects of 3 drugs AND 3 diet regiments (both are independent) on blood pressure 

• Ex: measuring mean # of texts/month in three age groups in three different countries 

CLASS:

more than 1 independent variable looking at 1 dependent variable

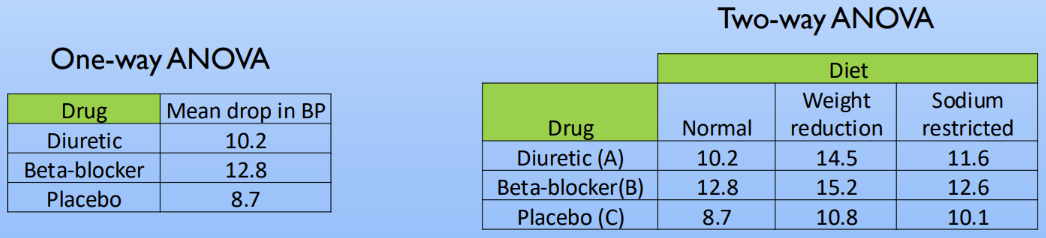
Describe a repeated-measures ANOVA

Repeated-measures ANOVA = one independent variable (multiple categories) and one dependent variable measured in the same subjects over multiple occasions 

• Analogous to the paired t-test (Within-subjects design) 

• Advantage of using repeated measures is that individual differences are controlled 

  • Lower error variance than in randomized experiment 

  • More powerful 

• Ex: measuring mean # of texts/month before school phone restrictions were implemented, after school phone restrictions were implemented, and after high school graduation 

CLASS:
SAME SAMPLE BEING LOOKED AT 3 DIFFERENT POINTS IN TIME

• when looking at more than 2 instances

Describe a Multivariate ANOVA (MANOVA)

Multivariate ANOVA (MANOVA) = one (or more) independent variables (with multiple categories) and two (or more) dependent variables 

• Includes MULTIPLE dependent variables 

• Detects pattens of values that result from the effects of multiple DVs that an ANOVA cannot detect 

• May be statistically significant when one or more of the ANOVAs are not significant, and vice verse 

• Ex: effects of 3 different medications on diastolic and systolic blood pressure (DBP, SDP) 

  • There is one IV with 3 levels (3 different drugs) 

  • There are two DVs (DBP & SBP) 

• Ex: measuring mean # of texts/month AND data usage/month in three age groups in three different countries 

CLASS:
MORE THAN 1 DEPENDENT VARIABLE

• doesn’t matter how many independent variables there are

• ex: attention, reaction time, and memory for 3 different tutoring styles

Interpret ANOVA statistical output in context of a research question

What is the use of a multiple comparison test

Multiple comparison test = post hoc because specific comparisons are decided after the ANOVA is completed  

• Good for exploration of outcome/general hypotheses (post hoc) 

  • Ex: Tukey’s, Newman-Keuls 

• Some are priori because specific comparisons are planned prior to data collection based on research rationale 

  • Ex: Bonferroni t-test 

What are the characteristics of various multiple comparison tests? (3)

1. Tukey (after)

2. Newman-Keuls (after)

3. Bonferroni (before)

Describe a Tukey

Tukey (after) = looks at a comparison of each group to each group to determine if the specific null for that pair can rejected 

• Establishes a “familywise” error rate, so that alpha identifies probability that one or more pairwise comparisons will be falsely declared significant 

• conservative 

Describe a Newman-Keuls

Newman-Keuls (after) = specifies type 1 error rate for each pairwise contrast, rather than for the family 

• The number of comparisons increases, the chances of type 1 error are greater than with a Tukey 

  • But is more POWERFUL. More likely to detect significant differences than Tukey 

Describe a Bonferroni

Bonferroni (Before) = Priori test that uses familywise error rate, therefore as # of comparisons increases, each comparison has to achieve a lower p-value to achieve significance 

• Protection against type 1 error 

• Considered fairly conservative tests with high p-values 

Interpret the results of a multiple comparison test in the context of the research question

Looking at picture:

Significance found in ANOVA, but the posttest found that there is no significance between 18-24 and 25 up group 

Steps to pick the appropriate statistical test

1. Is comparison planned or unplanned? 

   • If interested in exploring all possible combinations, unplanned contrasts should be used (Tukey or Newman-Keuls) 

   • If asking “is this particular difference significant?” then use planned comparison (Bonferroni) 

2. How important is the protection against type 1 and type 2 error? 

   • Each post-test offers different error control 

   • Newman-Keuls most powerful, but increases risk of type 1 error 

   • Tukey provides reasonable power and protection against type 1 error (but increased risk of type 2 error) 

3. Decisions should be based on the research question, not on which test is most likely to find significant differences! 

   • Have reason for picking what you did 

   • Choice is not always obvious