3.3 Derivatives of trigonometric Functions
1/9
Earn XP
Description and Tags
Before starting this section, you might need to review the trigonometric functions.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
10 Terms
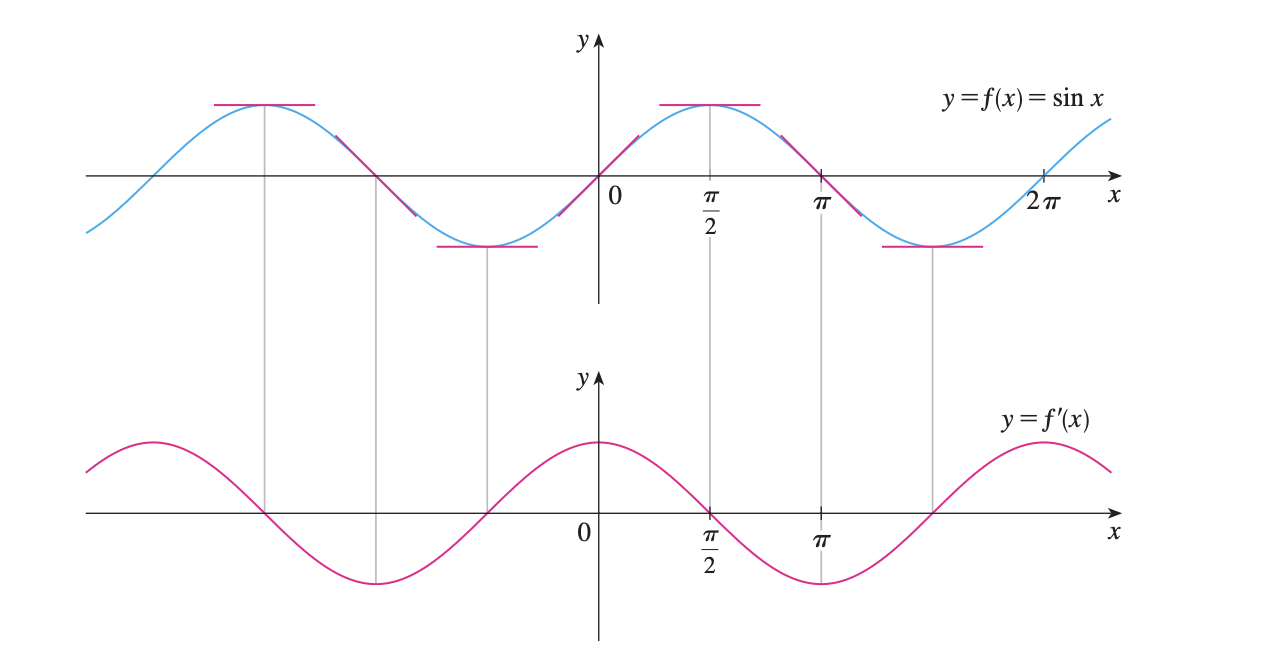
F(x)= sin x
If we sketch the graph of the function f (x)= sin x and use the interpretation of
f’ (x) as the slope of the tangent to the sine curve in order to sketch the graph of f9
Geometric proof of the fundamental trigonometric limit
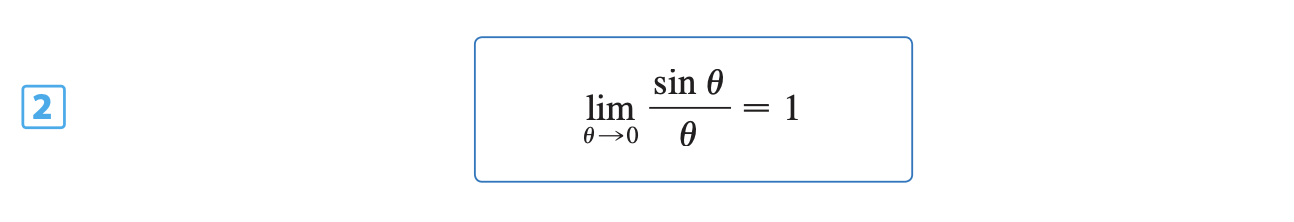

Derivative of ( sin x )
cos x
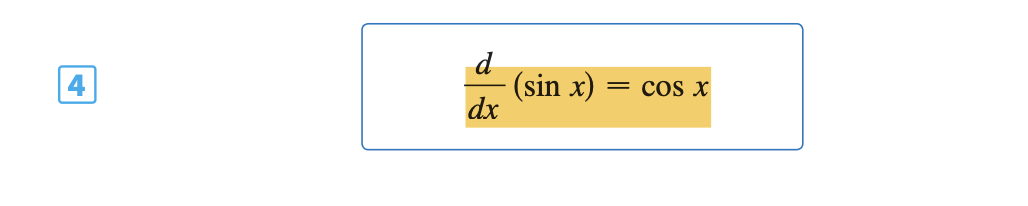
What is the derivative of (cos x) ?
-sin x
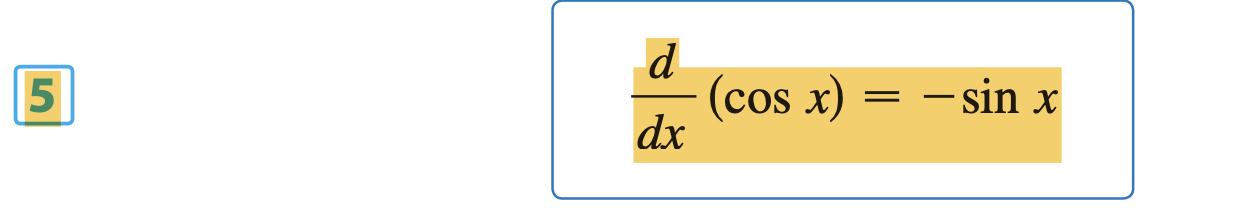
What is the derivative of ( tan x ) ?
sec ² x

What is the derivative of (csc x) ?
-csc x cot x

What is the derivative of ( sec x )?
sec x tan x
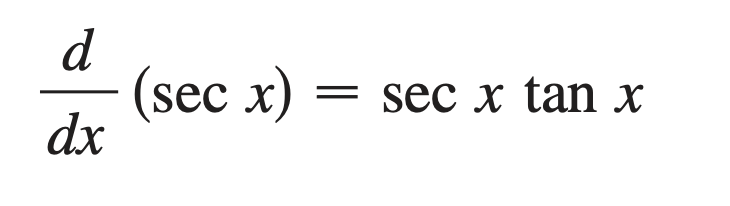
What is the derivative of (cot x) ?
- csc ² x
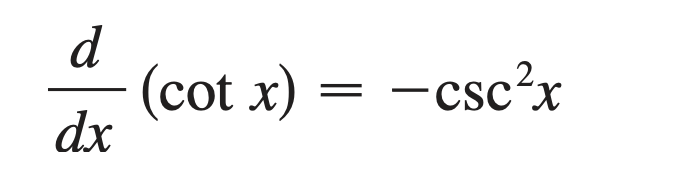
Derivatives of Trigonometric Functions
Trigonometric functions are often used in modeling real-world phenomena. In particular, vibrations, waves, elastic motions, and other quantities that vary in a periodic manner can be described using trigonometric functions.
