mathmetical analysis

операції з множинами

операції з множинами

обʼєднання
перетин
різниця
доповнення (через універсальну множину Х)
декартовий добуток

означення скінченної та нескінченної множини

скінченна - множина, яка складається зі скінченної кількості елементів
нескінченна - множина, яка складається зі нескінченної кількості елементів

означення функції (відображення f:X→Y)

це правило, яке кожному елементу x∈X, ставить у відповідність один і лише один елемент у∈Y

образ множини А

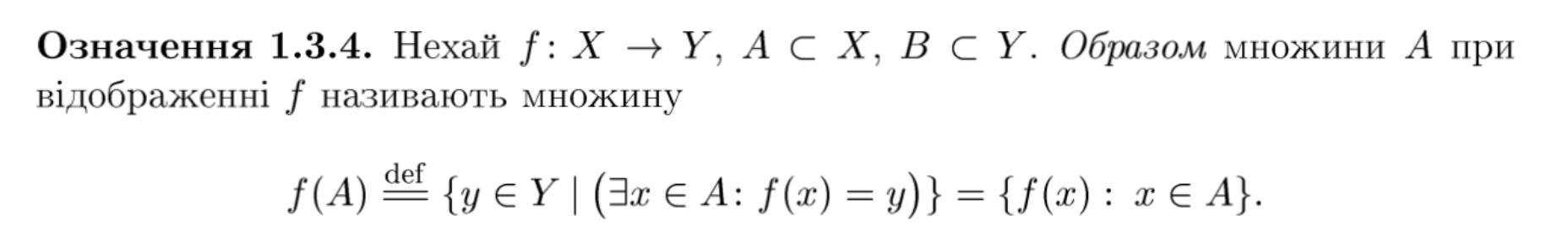
прообраз множини В

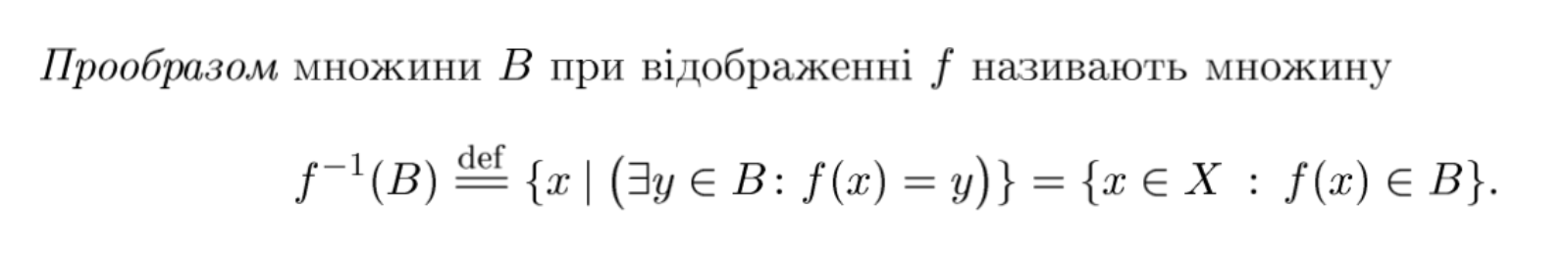
інʼєктивне відображення

для кожного х різні у (у набуває різних значень на всіх області визначення)

сюрʼєктивне відображення

х існує на всій області значень (для кожного у існує хоча б один х)

бієктивне відображення

інʼєктивне і сюрʼєктивне відображення водночас

умова існування оберненої функції

якщо існує бієкція даної функції

множини А і В називають рівнопотужними,

якщо існує бієкція f:A→B

(!!!) теорема(1.4.3) про обʼєднання зліченної кількості зліченних множин

обʼєднання зліченної кількості зліченних множин є зліченною множиною

(!!!) теорема(1.4.4) про існування незліченних множин

існують незліченні множини

множину A⊂R називають обмеженою зверху, якщо

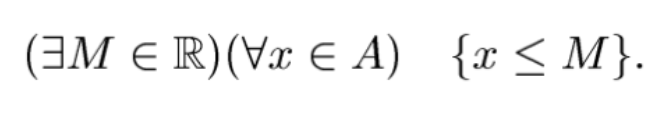
множину A⊂R називають обмеженою знизу, якщо

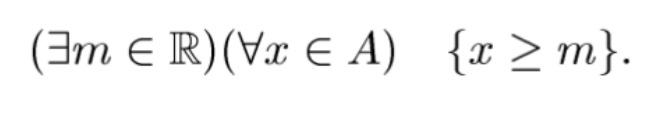
множину A⊂R називають обмеженою,

якщо вона обмежена і зверху, і знизу

означення максимального (найбільшого) елемента (с) множини A⊂R

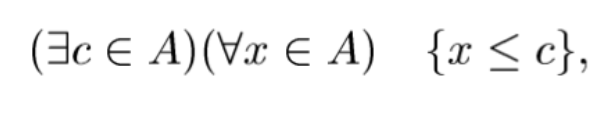
означення мінімального (найменшого) елемента (d) множини A⊂R

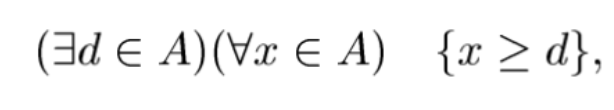
означення точної верхньої межі множини A⊂R

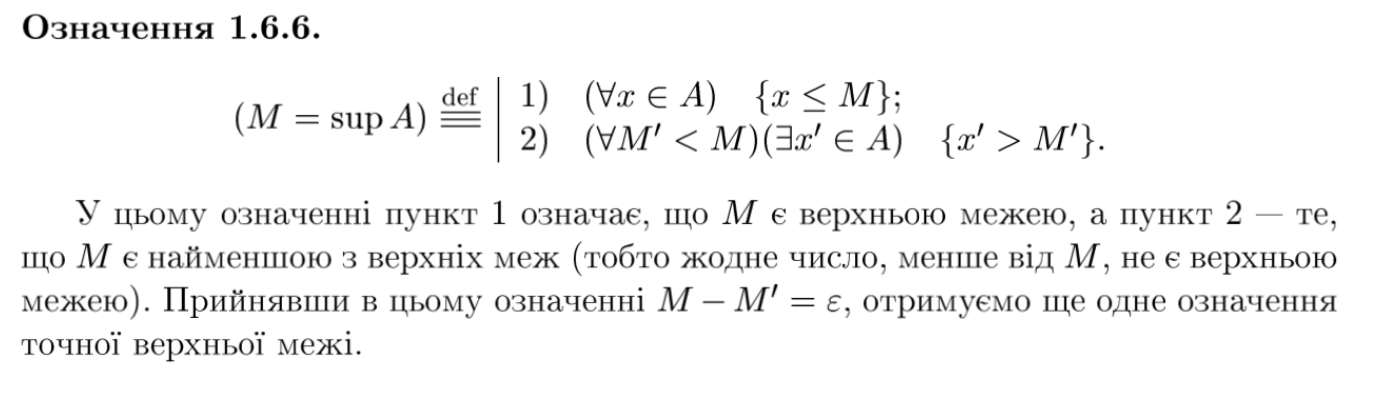
означення точної нижньої межі множини A⊂R

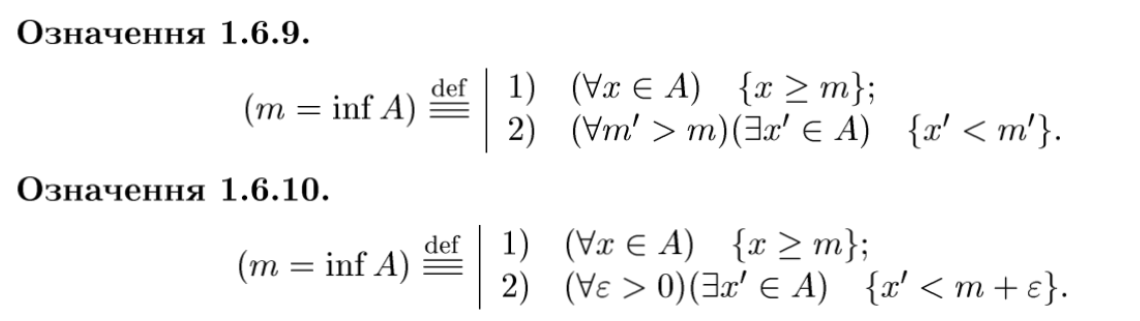
лема(1.6.1) принцип точної верхньої межі

кожна непорожня обмежена зверху підмножина множини дійсних чисел має точну верхню межу і до того ж лише одну

теорема(1.8.1) принцип Архімеда

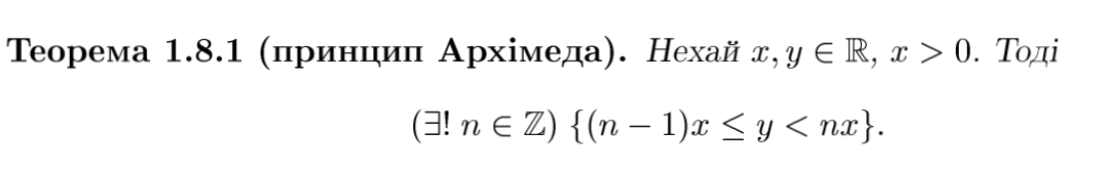
наслідки з принципу Архімеда

теорема(1.9.1) принцип вкладених відрізків

означення границі числової послідовності

ε-окіл числа а

(!!!) теорема(2.2.1) про єдиність границі послідовності

означення обмеженої послідовності (зверху/знизу/обм)

(!!!) теорема(2.2.2) про обмеженість збіжної послідовості

(!!!) теорема(2.2.8) про двох поліцаїв і пʼяного викладача з політєху

означення нескінченно малої послідовності

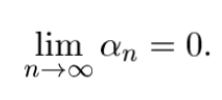
означення нескінченно великої послідовності

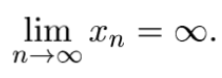
розширена множина дійсних чисел

множина дійсних чисел, включаючи {+∞} та {-∞}

невизначеності

(+∞) + (+∞) = +∞
∞ * ∞ = ∞
0/∞ = 0
∞/0 = ∞

означення зростаючої монотонної послідовності

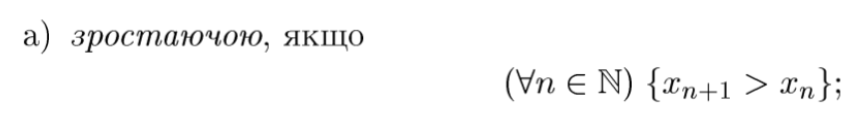
означення неспадної монотонної послідовності

означення спадної монотонної послідовності

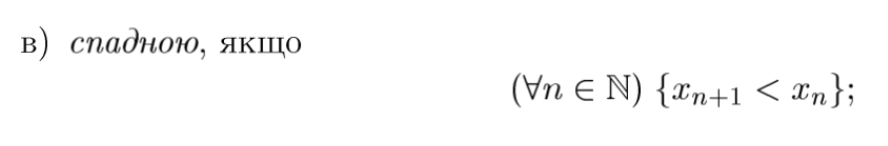
означення незростаючої монотонної послідовності

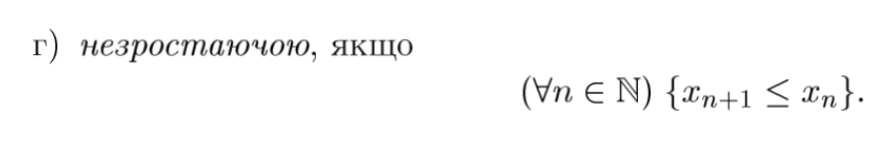
теорема(2.6.1) про збіжність монотонної обмеженої послідовності

монотонна обмежена послідовність має границю

означення підпослідовності послідовності

теорема(2.8.2) принцип Больцано-Вейєрштрасса

із будь-якої обмеженої послідовності можна виділити збіжну підпослідовність

означення фундаментальної послідовності

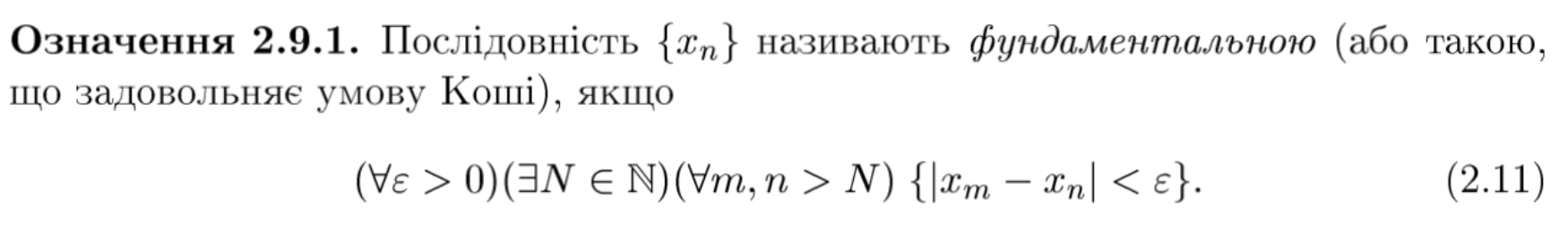
теорема(2.9.1) критерій Коші

для того, щоб послідовність збігалася, необхідноі достатньо, щоб вона була фундаментальною

означення границі функції

за Коші: (∀ε>0)(∃δ>0)(∀x∈(U⁰δ)(x₀)){f(x)∈Uε(A)}

(!!!) перша важлива границя

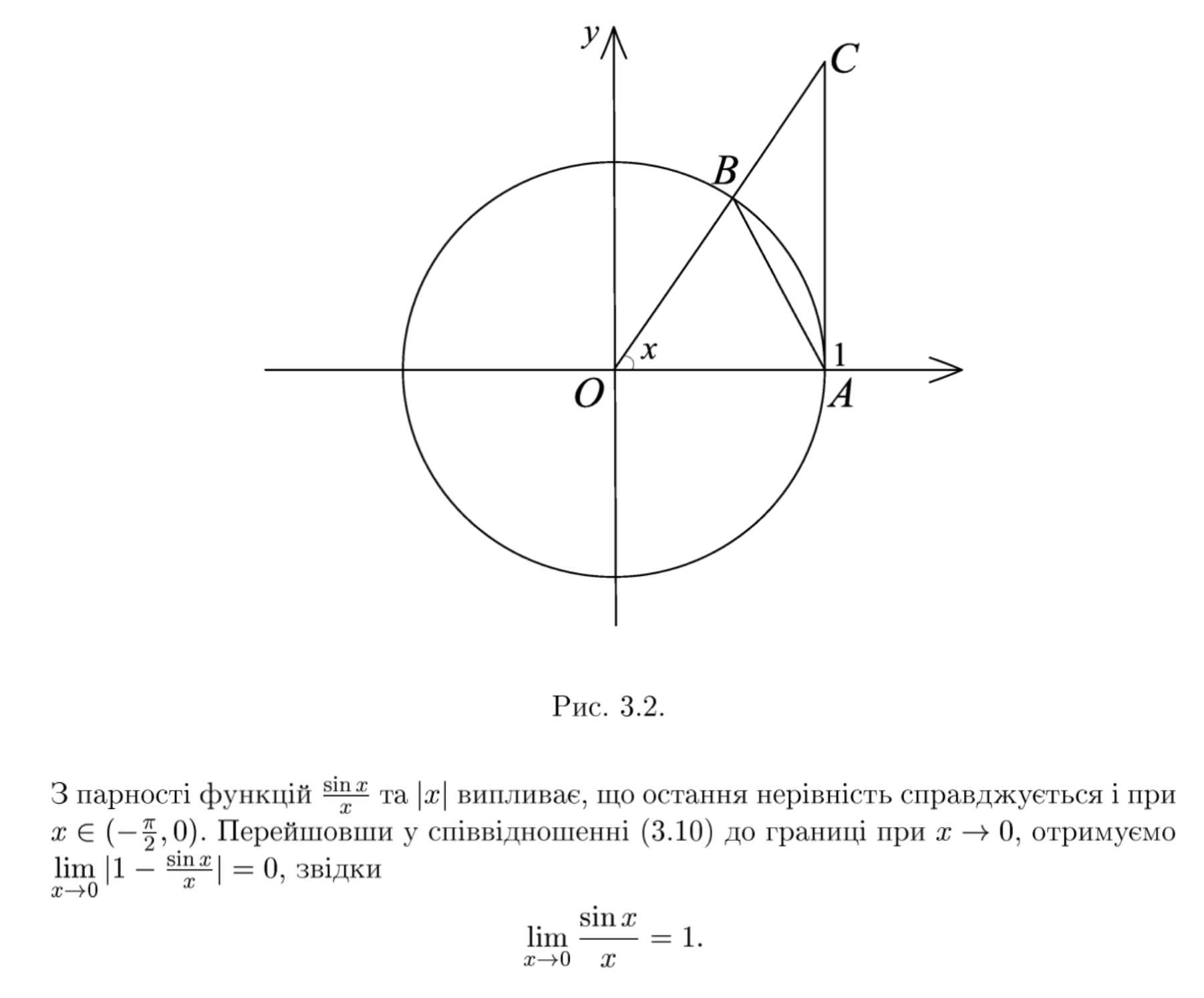
друга важлива границя

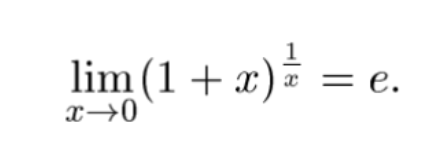
означення неперервної функції в точці х₀

приріст аргумента

∆x=x-x₀

приріст функції

∆y=f(x)-f(x₀)

означення неперервності в точці х₀ зліва/справа

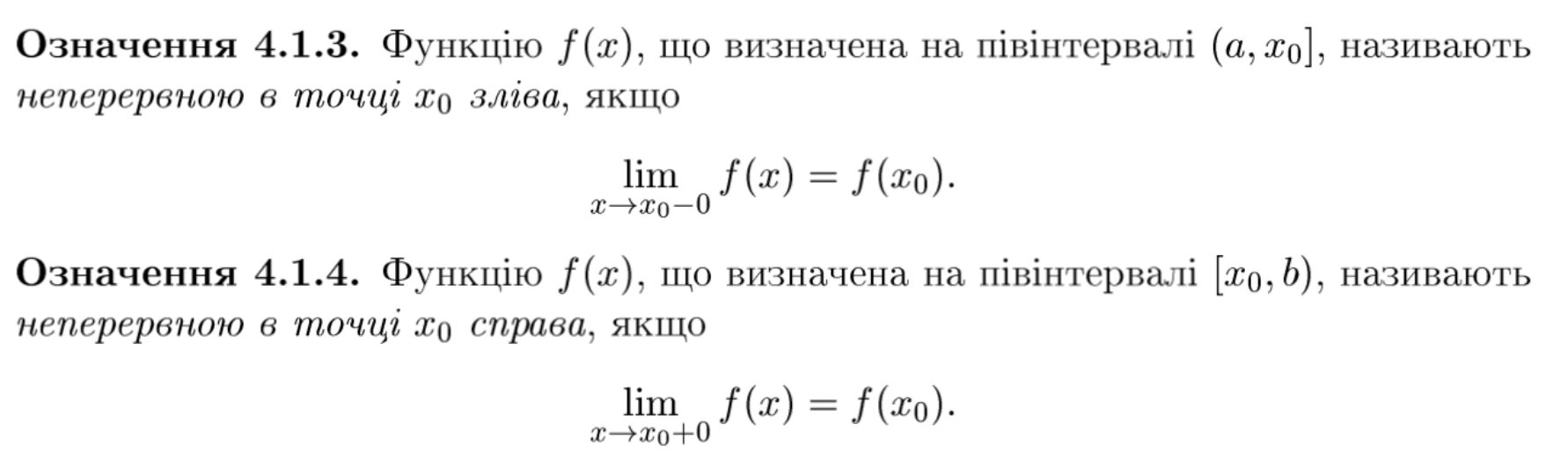
означення точки розриву на інтервалі (a,b)

означення точки розриву першого роду

це точка, яка
1) є точкою розриву
2) існують скінченні односторонні границі

→ пр: y = sgnx

означення точки усувного розриву

це точка розриву першого роду, величина стрибка(різниця право і лвосторонньої границь) якої = 0
→ пр: y = (x+3)/(x²+x-6), x=-3

означення точки розриву другого роду

це точка, яка
1) є точкою розриву
2) одна з односторонніх границь, або не існує, або = ∞
→ пр: y= x/(x²-1)

(!!!) теорема(4.4.1) Вейерштрасса

Якщо функція f(x) є неперервною на відрізку [a,b], то вона обмежена і досягає на ньому своїх верхньої і нижньої точних меж, тобто

(!!!) теорема(4.4.2) Больцано-Коші

нехай функція f(x) неперервна на відрізку [a,b], f(a)=A, f(b)=B; тоді для будь-якого числа С, що лежить між А та В, знайдеться точка x₀∈[a,b] така, що f(x₀)=C

означення рівномірно неперервної функції

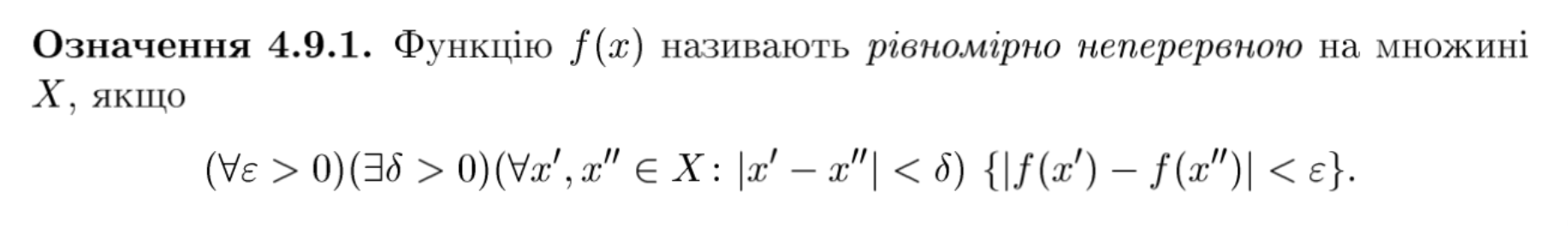
теорема(4.9.1) Кантора

(f(x) - неперервна на [a,b]) ↔ (f(x) - рівномірно неперервна на [a,b])

означення похідної функції

геометричний зміст похідної

k(∆x) = ∆y/∆x = tga(∆x)

означення диференційовної функції в точці х₀

(!!!) теорема(5.3.1) про похідну диференційовної функції

для того, щоб функція f(x) була диференційовною в точці х₀, необхідно і досить, щоб вона мала в цій точці похідну

(!!!) теорема(5.3.2) про неперервність диференційовної функції

якщо функція f(x) диференційовна в точці х₀, то вона неперервна в точці х₀

(!!!) теорема(5.4.1) арифметичні дії з функціями

формула Лейбніца

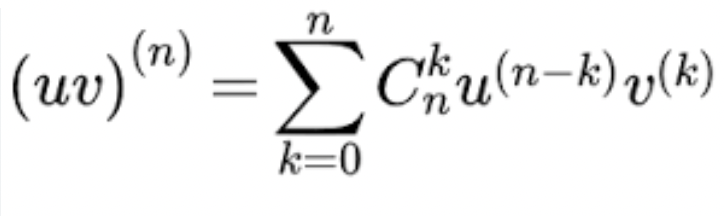
(!!!) теорема(6.1.1) про зростання і спадання диференційовної функції

(!!!) теорема(6.1.2) Ферма

(!!!) теорема(6.2.1) Ролля

(!!!) теорема(6.2.2) Лагранжа

(!!!) теорема(6.2.3) Коші

(!!!) наслідок 1 з теореми Лагранжа

(!!!) наслідок 2 з теореми Лагранжа

(!!!) теорема(6.5.1) перше правило Лопіталя

(!!!) теорема(6.6.1) формула Тейлора

(!!!) теорема(7.2.1) перша достатня умова екстремуму

(!!!) теорема(7.2.2) друга достатня умова екстремуму

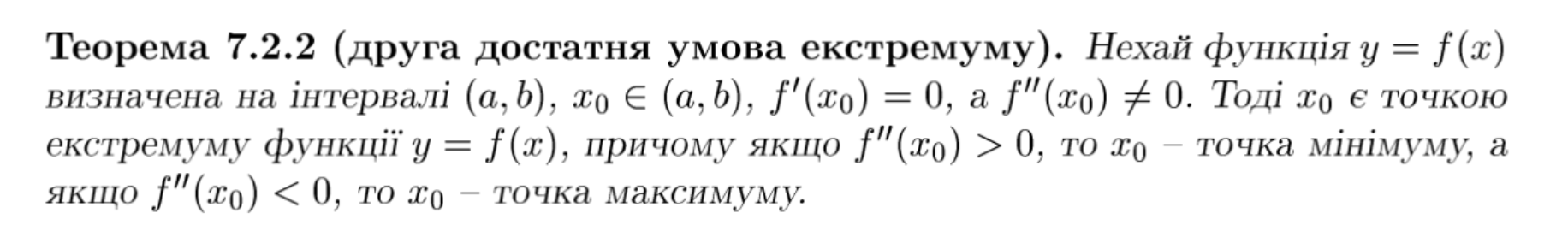
означення опуклої функції

функцію f(x), що визначена на інтервалі (a,b), називають опуклою вниз (опуклою вгору), якщо графік функції лежить не нижче (не вище) від совєї дотичної, проведеної в будь-якій точці інтервалу (a,b)

(!!!) теорема(7.3.1) про характер опуклості функції

теорема (7.4.1) перша двостатня умова перегину

теорема (7.4.2) друга двостатня умова перегину

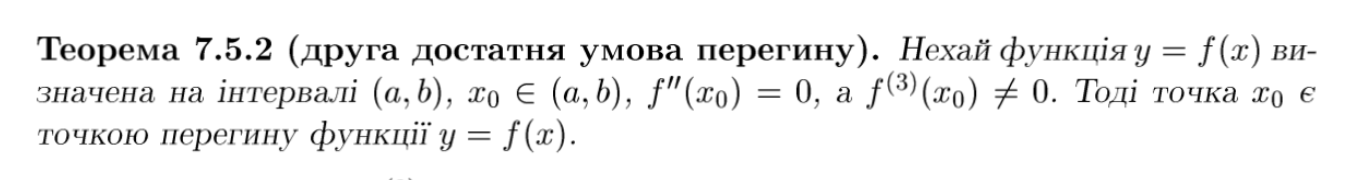
означення вертикальної асимптоти

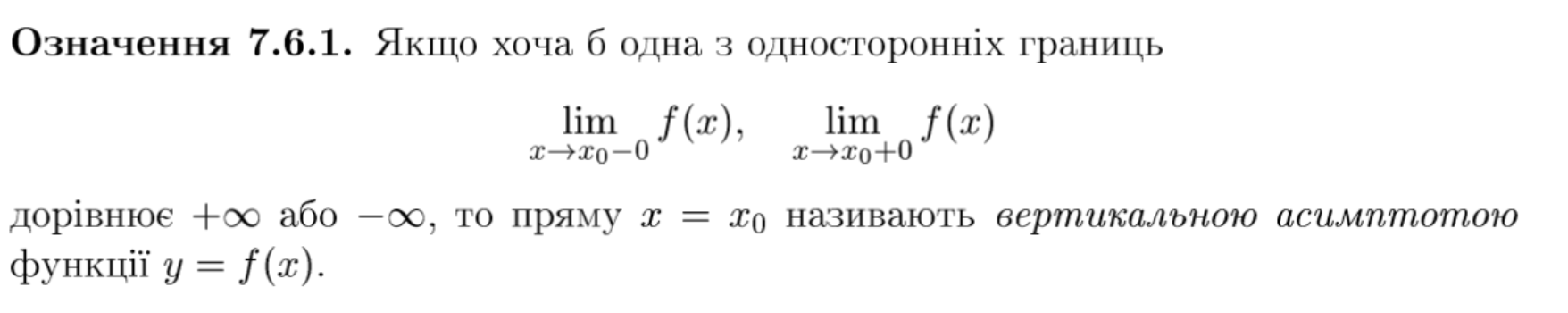
означення похилої асимптоти