W7: Numeric Prediction and Regression Methods

Numeric prediction

Supervised learning method used in business analytics to predict continuous values.

• Unlike classification, which predicts categories, ___ estimates numerical outcomes.

How It Works:

• Uses historical data with known values.

• Learns patterns to predict new, unseen data.

• Accuracy depends on data quality, predictor selection, and model choice.

Key Applications:

• Insurance: Estimating medical expenses for setting premiums.

• Retail: Forecasting sales and managing inventory.

• Real Estate: Predicting property values based on size, location, etc.

Regression Methods Overview

key to numeric prediction, modeling the relationship between a numeric target variable and one or more predictors.

Why It Matters in Business:

• Provides predictions and insights into key factors.

• Helps decision-makers understand what influences outcomes.

Types of Regression:

• Linear Regression

• Advanced Methods

Linear Regression

Assumes a straight-line relationship.

• Simple ____ Regression: One predictor.

• Multiple ___ Regression: Multiple predictors.

Advanced Methods

Non-linear Regression: Captures complex patterns.

Regression Trees: Uses decision trees for predictions.

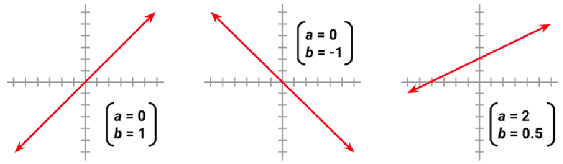
Simple Linear Regression

models the relationship between one independent variable (X) and one dependent variable (Y) using a straight line.

• Positive slope means y increases as x increases.

• Negative slope means y decreases as x increases.

Equation: y = a + bx

• y: Dependent variable (predicted value).

• x: Independent variable.

• a: Intercept (y-value when x = 0)

• b: Slope (rate of change in y for each unit change in x).

The goal is to find the best-fitting line that minimizes prediction error.

• works with one predictor, while multiple regression includes several factors

Ordinary Least Squares Estimation

Finds the best-fit line in linear regression, and minimizes the sum of squared errors between actual and predicted values.

• where x̄ and ȳ are the means of x and y.

• Once a and b are calculated, the equation y = a + bx can be used for predictions.

Multiple Linear Regression

predicts a dependent variable (y) using multiple independent variables (x₁, x₂, ..., xᵢ).

y = β₀ + β₁x₁ + β₂x₂ + ... + βᵢxᵢ +ε

• y is the dependent variable,

• x₁, x₂, ..., xᵢ are the independent variables,

• β₀ is the intercept,

• β₁, β₂, ..., βᵢ are the coefficients for each independent variable, and

• ε is the error term(unexplained variation

Advantages:

• Accounts for multiple factors

• More accurate predictions

• Helps identify key influencers

Multiple Linear Regression (Key components)

Beta Coefficients (β)

Expenses

P-Values

R-Squared (R²)

Overfitting Risk

Beta Coefficients (β)

coefficients indicate the estimated increase in expenses for an increase of one in each of the variables, assuming all other values are held constant.

• Intercept is of little value alone because it is impossible to have values of zero for all features

Expenses

-11836.117831 + 256.402924*age + 335.414456*bmi + 472.939931*children - 47.692891*sexmale + 23435.046128*smokeryes -561.353117*regionnorthwest – 995.537125* regionsouthest – 798.824371* regionsouthwest

P-Values

For each estimated regression coefficient, the p-value, assess whether a predictor significantly impacts the dependent variable.

• Small p-values suggest that the true coefficient is very unlikely to be zero, which means that the variable is extremely unlikely to have no relationship with the dependent variable.

• p-values less than the significance level (<0.05) are considered statistically significant.

R-Squared (R²)

The multiple R-squared value provides a measure of how well our model as a whole explains the values of the dependent variable.

• The model explains nearly 73 percent of the variation in the dependent variable.

Overfitting Risk

A very high R² on training data may indicate overfitting, meaning the model might not perform well on new data.

Evaluation Metrics for Numeric Prediction

evaluate regression model accuracy:

• Mean Absolute Error (MAE)

• Root Mean Squared Error (RMSE)

Mean Absolute Error (MAE)

measures the average absolute difference between predicted and actual values:

• It treats all errors equally and is easy to interpret.

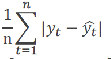
Root Mean Squared Error (RMSE)

gives a relatively high weight to large errors.

• should be more useful when large errors are particularly undesirable.

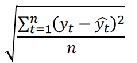
Improving Model Performance

While standard multiple linear regression provides a solid foundation for numeric prediction, we can often enhance model performance by incorporating more complex relationships.

• Several approaches can help us capture non-linear patterns and interactions that might exist in the data.

Adding Non-linear Relationships

• Linear regression assumes a straight-line relationship between variables, but this is not always accurate. For example, medical costs may increase more rapidly as people age.

• To handle this, we can add squared or cubic terms to the model. For instance, using age² (age squared) helps capture the increasing effect of age on costs. In one case, the coefficient for age² was about 2.89, meaning costs rise faster for older individuals.

• This approach improves the model’s accuracy in reflecting real-world patterns.

Converting Numeric Variables to Binary Indicators

• Sometimes, a numeric variable’s effect on the outcome is not gradual but occurs at a specific threshold. In such cases, converting it into a binary variable can improve model accuracy.

• For example, BMI may have little impact on medical costs in the normal range but significantly increases expenses for obese individuals (BMI ≥30). By creating a binary obesity indicator (1 if BMI ≥30, 0 otherwise), we can better capture this threshold effect.

• In our medical expenses model, being obese was linked to an additional cost of about $2,810 beyond BMI’s linear effect. This approach highlights key thresholds where variables have a strong impact.

Incorporating Interaction Effects

What happens when two features together influence the dependent variable?

• In regression models, some variables influence each other, meaning their combined effect is greater than their individual impacts.

• For example, both smoking and obesity raise medical costs, but together, they may lead to even higher expenses. To capture this, we add an interaction term (smoker × obese) in the model.

• Our analysis found that smoking increased medical expenses by about $13,445 for non-obese individuals. However, for obese smokers, the cost increased by $33,461 due to a $20,016 interaction effect. This shows why considering interactions is crucial in regression models.

Improved Regression Model

Using domain knowledge, we refined our regression model by:

• Adding a non-linear term for age

• Creating an obesity indicator

• Including an interaction between obesity and smoking

Regression Trees for Numeric Prediction

• Linear regression models impose a fixed structure on data relationships, while regression trees offer a more flexible approach.

• Regression trees split data into subgroups based on predictor values, using the mean target value in each subgroup as the prediction. They select splits to minimize prediction error, typically using squared differences.

• Unlike linear regression, regression trees do not assume a specific relationship between variables. They naturally capture non-linear patterns and interactions, making them useful for complex datasets.

• For example, in predicting medical expenses, a regression tree might first split data by smoking status, then further divide non-smokers by age or BMI, with each final group providing a specific expense estimate.

Comparing Different Regression Methods

When evaluating different regression approaches, we need to consider both their predictive performance and other practical factors such as interpretability, computational requirements, and robustness to outliers.

For our medical expenses prediction problem, the comparison of different models showed interesting results:

• • Basic linear model with age² term: MAE =3,953.76, RMSE =5,707.45

• • Model with binary obesity indicator: MAE =4,086.90, RMSE =5,658.93

• • Model with interaction effects: MAE =2,309.13, RMSE =4,097.09

• • Regression tree: MAE =2,717.52, RMSE =4,462.88

The model incorporating interaction effects performed best in terms of both MAE and RMSE, highlighting the importance of capturing how variables work together to influence the outcome. The regression tree also performed well, particularly compared to the simpler linear models

Choosing the Right Regression Approach

Regression analysis is a key tool in business analytics, helping organizations make data-driven decisions.

The choice of method depends on data complexity and business needs.

• Simple linear regression: works with one predictor, while multiple regression includes several factors.

• Enhanced models: with non-linear terms, binary indicators, and interactions improve accuracy.

• Regression trees: handle complex patterns automatically, making them useful when relationships are unclear.

Comparing models using metrics like MAE and RMSE helps select the best approach, balancing accuracy, interpretability, and efficiency. As data and computing power grow, regression remains essential for extracting insights and guiding decisions.