Basic Integration Rules, Pythagorean Identities, and some more

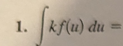
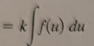
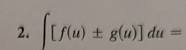
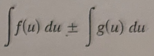
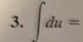
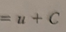
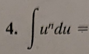
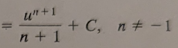
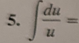
ln|u| + C

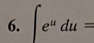
e^u + C

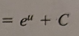
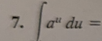
(1/ln|a|)a^u + C

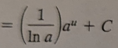
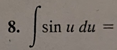
-cos(u) + C

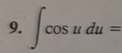
sin(u) + C

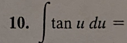
-ln|cos(u)| + C

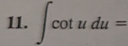
ln|sin(u)| + C

ln|sec(u)+tan(u)| + C

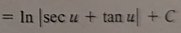
-ln|csc(u)+cot(u)| + C

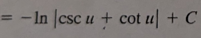
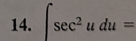
tan(u) + C

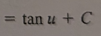
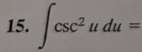
-cot(u) + C

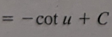
sec(u) + C

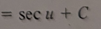
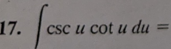
-csc(u) + C

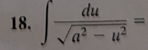
arcsin(u/a) + C

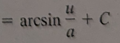
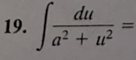
(1/a)arctan(u/a) + C

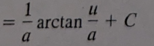
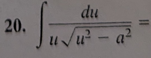
(1/a)arcsec(|u|/a) + C

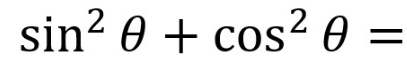
1

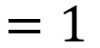
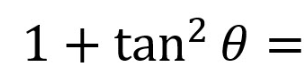
sec²(theta)

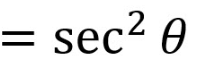
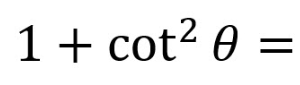
csc²(theta)

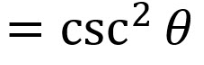
sin(2x) =

2sin(x)cos(x)

cos(2x) =

cos²(x)-sin²(x)

cos²(x) =

1/2(1+cos(2x))

sin²(x) =

1/2(1-cos(2x))

Integration by Part formula

∫udv = uv-∫vdu

∫sin³(x)dx =

∫sin²(x)sin(x)dx = ∫(1-cos²(x))sin(x)dx

∫sin²(2x)cos²(2x)dx

∫(1/2(1-cos(4x))*(1/2(1+cos(4x))dx

∫sec⁴(3x)tan(3x)dx =

∫sec²(3x)sec²(3x)tan(3x)dx = ∫(1+tan²(3x)tan(3x)sec²(3x)dx

a³-b³ =

(a-b)(a²+ab+b²)

a³+b³ =

(a+b)(a²-ab+b²)

Complete the square
x²+10x+5 = 0

x²+10x+(b/2)² = -5+(b/2)²
x²+10x+25 = -5+25
(x+5)² = 20

∫xln(x)dx

(1/2)x²ln(x)-(1/4)x²+C