Lecture 2: Uncertainty

ω

represents every possible situation can be thought of as a world; its probability is P(ω)

0 < P(ω) < 1

every value representing probability must range between 0 and 1.

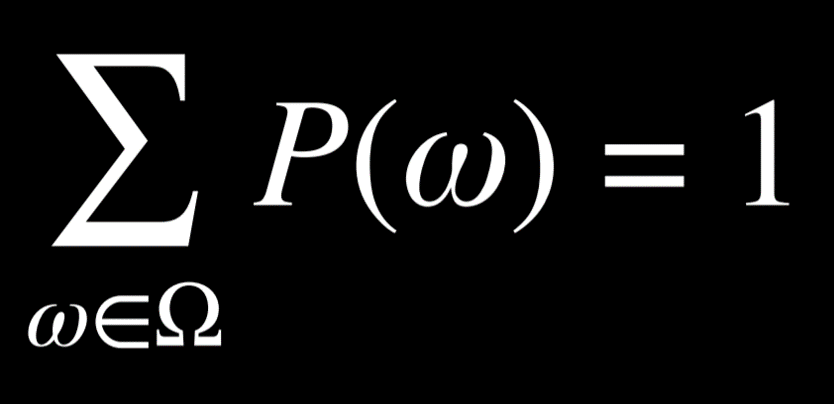
The probabilities of every possible event, when summed together, are equal to 1.

Unconditional Probability

the degree of belief in a proposition in the absence of any other evidence

Conditional Probability

the degree of belief in a proposition given some evidence that has already been revealed

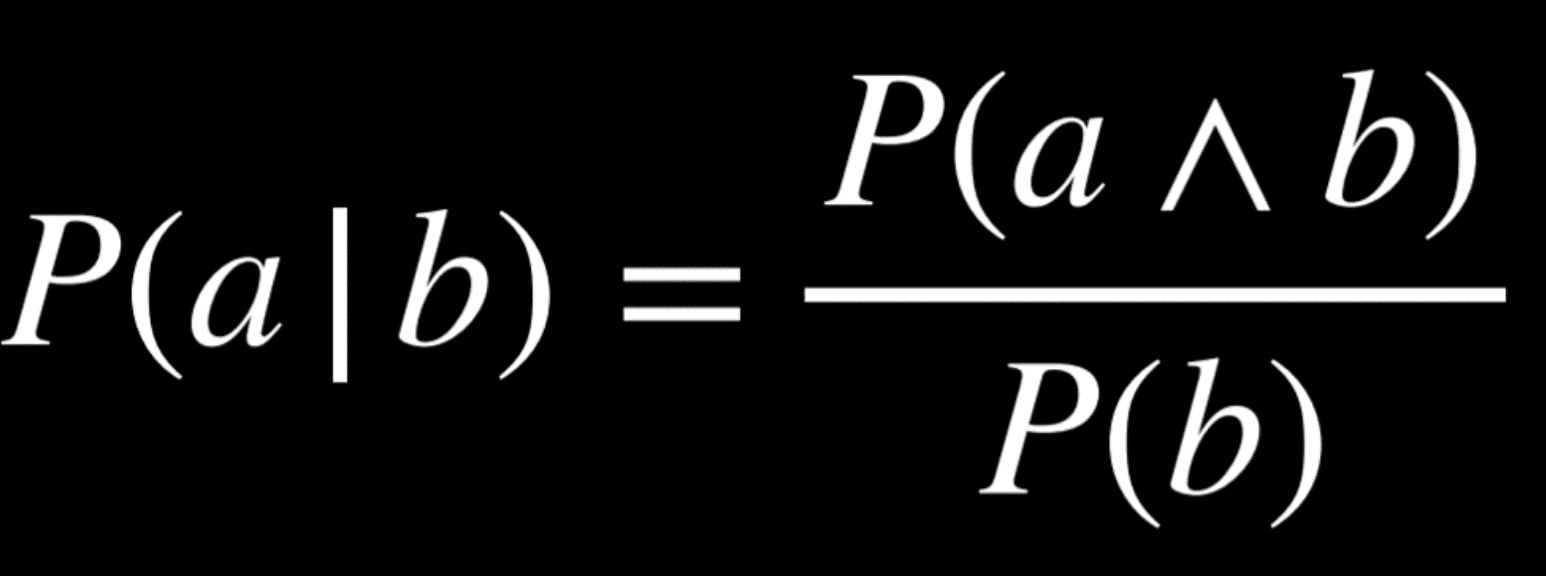
Random Variable

a variable in probability theory with a domain of possible values that it can take on

Independence

the knowledge that the occurrence of one event does not affect the probability of the other event; events a and b are independent if and only if the probability of a and b is equal to the probability of a times the probability of b: P(a ∧ b) = P(a)P(b).

Bayes Rule

commonly used in probability theory to compute conditional probability; says that the probability of b given a is equal to the probability of a given b, times the probability of b, divided by the probability of a.

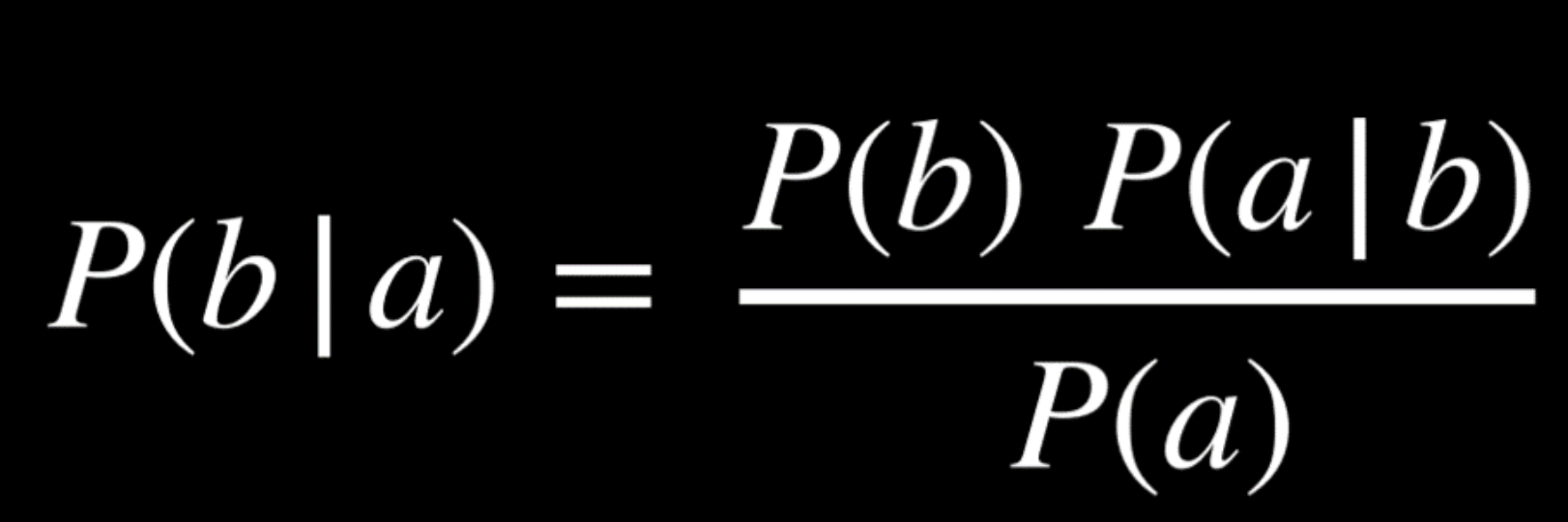
Joint Probability

the likelihood of multiple events all occurring.

Negation

P(¬a) = 1 - P(a); Probability Rule that stems from the fact that the sum of the probabilities of all the possible worlds is 1, and the complementary literals a and ¬a include all the possible worlds

Inclusion-Exclusion

P(a ∨ b) = P(a) + P(b) - P(a ∧ b); Probability Rule that can interpreted in the following way: the worlds in which a or b are true are equal to all the worlds where a is true, plus the worlds where b is true. However, in this case, some worlds are counted twice (the worlds where both a and b are true)). To get rid of this overlap, we subtract once the worlds where both a and b are true (since they were counted twice).

Marginalization

P(a) = P(a, b) + P(a, ¬b); Probability Rule where The idea here is that b and ¬b are disjoint probabilities. That is, the probability of b and ¬b occurring at the same time is 0. We also know b and ¬b sum up to 1. Thus, when a happens, b can either happen or not. When we take the probability of both a and b happening in addition to the probability of a and ¬b, we end up with simply the probability of a.

Marginalization (Random Variables)

• Left side: “The probability of random variable X having the value xᵢ.”

• Right Side = idea of marginalization

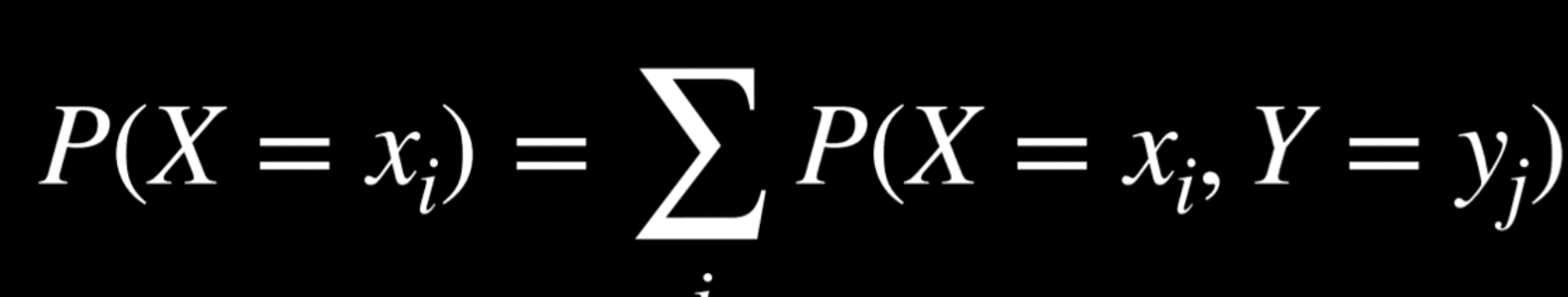
Conditioning

P(a) = P(a | b)P(b) + P(a | ¬b)P(¬b); probability rule with a similar idea to marginalization. The probability of event a occurring is equal to the probability of a given b times the probability of b, plus the probability of a given ¬b time the probability of ¬b.

Bayesian Networks

a data structure that represents the dependencies among random variables

Query X

Inference property; the variable for which we want to compute the probability distribution.

Evidence variables E

Inference Property; one or more variables that have been observed for event e

Hidden variables Y

Inference property; variables that aren’t the query and also haven’t been observed.

The goal

Inference property; calculate P(X | e).

Inference by enumeration

a process of finding the probability distribution of variable X given observed evidence e and some hidden variables Y.

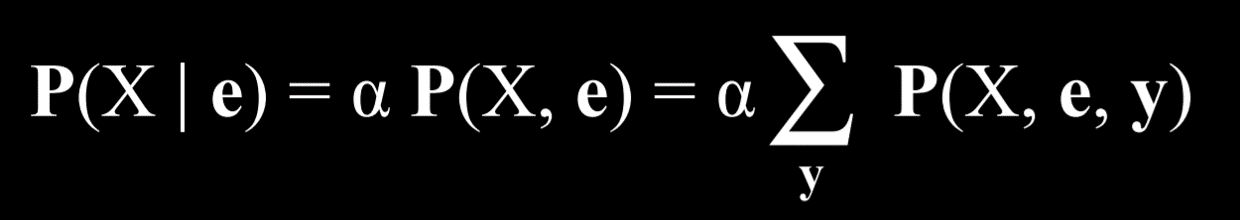
Sampling

a technique of approximate inference where each variable is sampled for a value according to its probability distribution.

Likelihood Weighting

The Markov assumption

an assumption that the current state depends on only a finite fixed number of previous states.

Markov Chain

a sequence of random variables where the distribution of each variable follows the Markov assumption. That is, each event in the chain occurs based on the probability of the event before it.

Hidden Markov Model

a type of a Markov model for a system with hidden states that generate some observed event. This means that sometimes, the AI has some measurement of the world but no access to the precise state of the world. In these cases, the state of the world is called the hidden state and whatever data the AI has access to are the observations

Sensor Markov Assumption

assumes only the hidden state affects an observation

Tasks that can be completed with hidden Markov Models