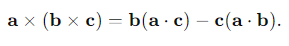The vector product(2)
1/25
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
26 Terms
What is the formula for the vector product a×b?
θ= the angle between the vectors
n^= the unit vector perpendicular to both a and b.
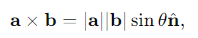
How do you show that 3 vectors are coplanar(lie in the same plane)?
The result of the triple scalar product will=0 if they’re coplanar
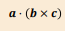
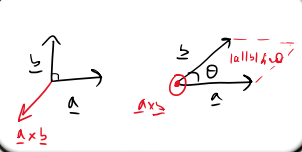
What is the result of the vector (cross) product a×b?
The result of the vector product is a vector that has:
Magnitude ∣a∣∣b∣sinθ|, corresponding to the area of the parallelogram formed by a and b
Direction perpendicular to both a and b, determined by the right-hand rule.
How is the direction of the result of a vector product determined?
The direction is perpendicular to both vectors a and b
It is determined using the right-hand rule.
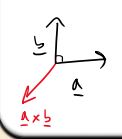
What does the magnitude of the vector product a×b represent?
The magnitude represents the area of the parallelogram formed by vectors a and b.
What is the distributive property of the vector product?
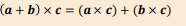
What are the properties of the vector product?
Distributive
Anticommutative
Non-associative
What is the anticommutative property of the vector product?

Is the vector product associative?
No, the vector product is non-associative:
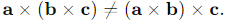
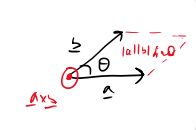
What is the vector product of a vector with itself?
The vector product of a vector with itself is zero since the angle θ=0
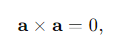
If a×b=0, what can we conclude about the relationship between a and b?
a is parallel or antiparallel to b
What is the result of the vector product for the Cartesian basis vectors?
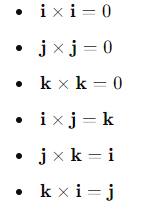
How do you compute the vector product of two vectors in Cartesian components?
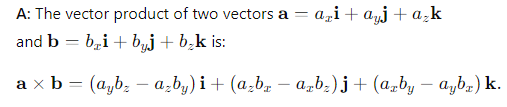
How can you express the vector product of two vectors in a more compact form?
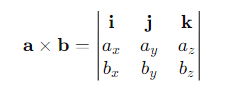
What is the scalar triple product of three vectors a, b, c?
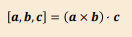
What type of quantity does the scalar triple product result in?
The scalar triple product results in a scalar quantity.
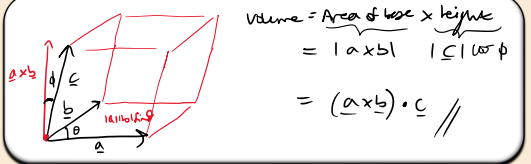
How can the scalar triple product be interpreted geometrically?
The scalar triple product represents the volume of a parallelepiped whose edges are given by the vectors a, b and c
What does it mean if the scalar triple product (a×b)⋅c =0?
If the scalar triple product equals zero, then the vectors a, b and c are coplanar.
Is the scalar triple product commutative?
Yes, the scalar triple product is cyclically commutative:
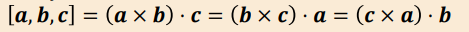
What happens if there are duplicated vectors in the scalar triple product?
If any vector is duplicated, the scalar triple product is zero
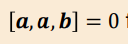
How do you compute the scalar triple product using the components in the Cartesian basis set?
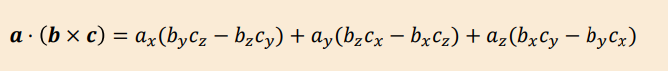
How can the scalar triple product be expressed in determinant form?
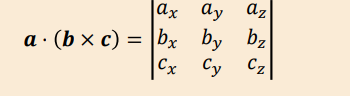
What is the vector triple product of three vectors a, b and c?
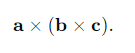
What is the geometric property of the resultant vector in a vector triple product?
The resultant vector is perpendicular to both a and b×c
Additionally, b×c is perpendicular to both b and c.
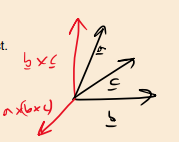
Where does the resultant vector of the vector triple product lie?
The resultant vector lies in the plane containing b and c, and is a linear combination of b and c.
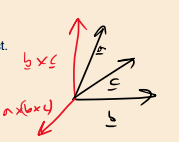
How can the vector triple product be expressed in a simplified form?
This is known as the "bac cab" rule.