math-125 final

integration by parts

∫u dv = uv - ∫v du

LIATE to assign u: Logarithmic functions, Inverse trig functions, Algebraic functions, Trig functions, Exponential functions

sin(θ) = x

√(a²-x²)

tan(θ) = x

√(a²+x²)

sec(θ) = x

√(x²-a²)

partial fraction decomposition

a way to simplify any rational function by splitting the denominator into several lower-degree denominators and solving for the numerators

steps: 1) factor denominator; 2) set up A, B, and C; 3) pick values of x to find A, B, and C; 4) integrate each fraction

improper

an integral is ____ if…

1) it has an unbounded region of interpretation

2) it has an integrand that is unbounded somewhere within the region of integration (lower bound, upper bound, or unbounded within the region

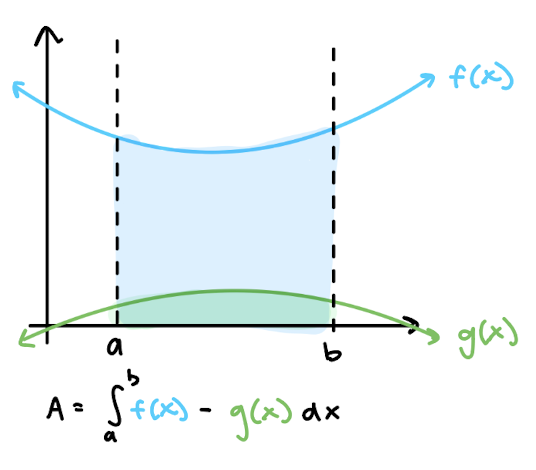
area between curves

top function - bottom function

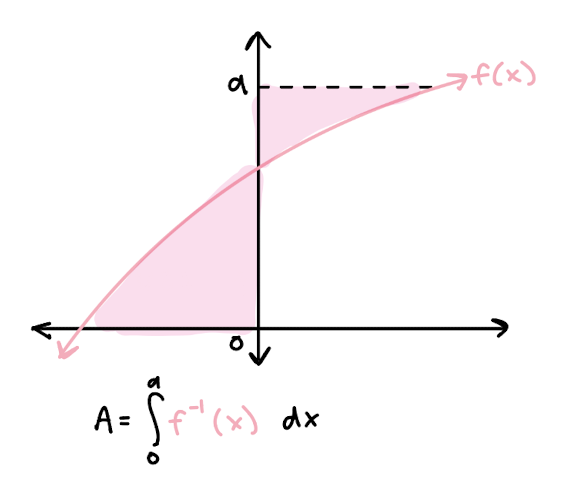
area between function and y-axis

put into terms of y and integrate

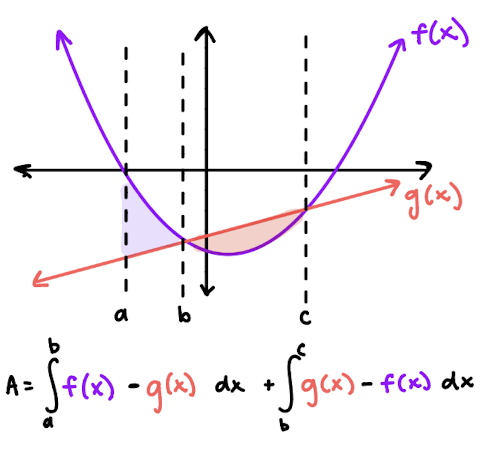
area between curves that intersect

set up two integrals — one before intersection point, one after intersection point

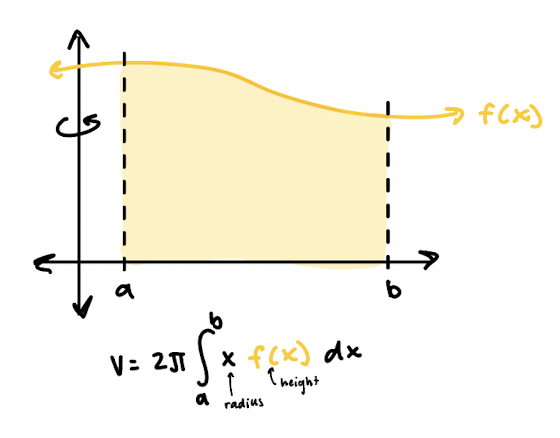
disk method

if f is continuous over a region [a, b] and the solid is obtained by rotating the function about the x-axis, the volume of the solid is…

washer method

the area of cross section = A_outer - A_inner; use when “slices” are perpendicular to axis of rotation

shell method

rotation around the y-axis; use when “slices” are parallel to axis of rotation

arc length

using pythagorean theorem to find small segment lengths of a function

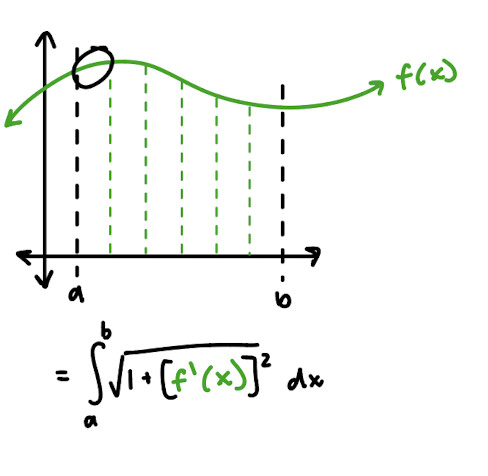
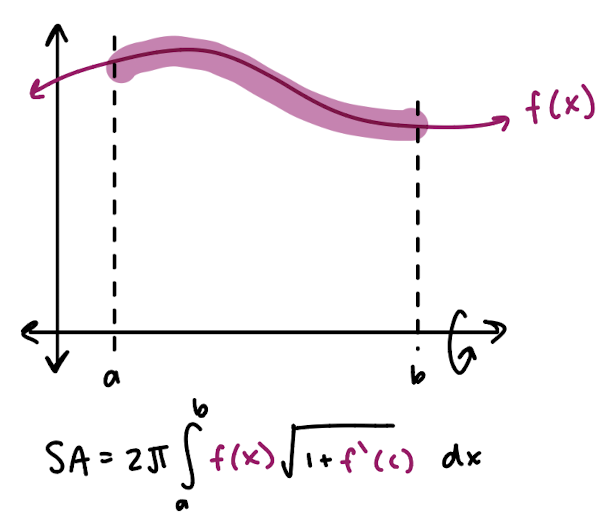
surface of revolution

if f(x) is a continuous, differentiable function and we rotate it around the x-axis, we create a surface of revolution

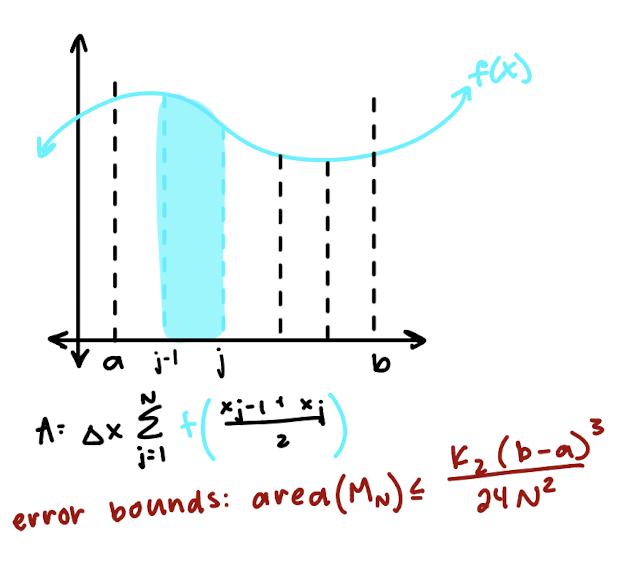
midpoint rule

approximate area by summing rectangles of height f(c_j) and base Δx, where c_j = middpoint between x_j-1 and x_jf

trapezoidal rule

approximate area by summing trapezoids

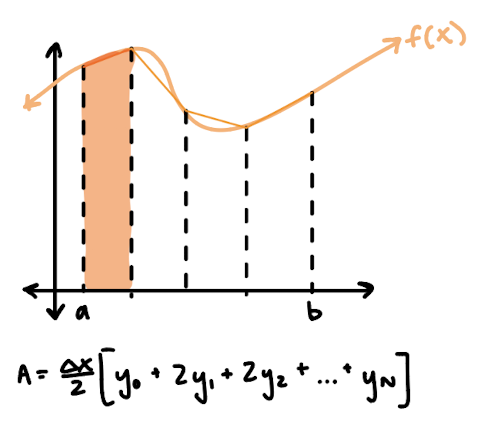
simpson’s rule

fit a parabola to each pair of 2 consecutive intervals and compute area underneath

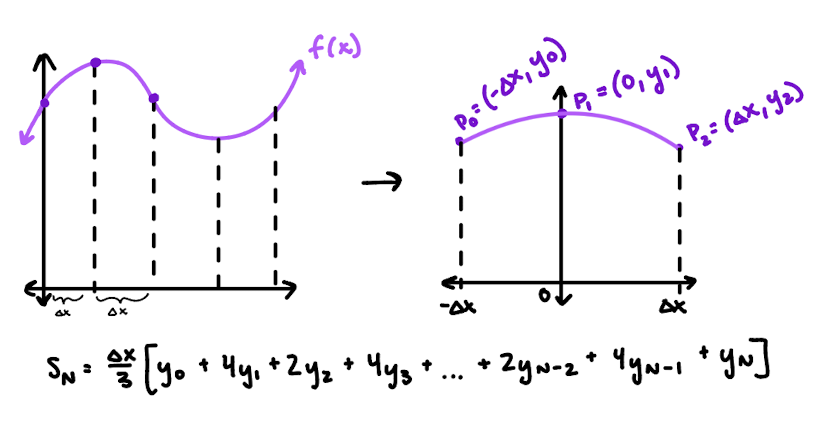
sequence

{a_n}

an ordered collection of numbers defined by some function f on a set of sequential integers

recursive sequences

sequence where the next term is based on previous terms

Fibonaces Sequence: F₀ = 0, F₁ = 1, F_n = F_n-2 + F_n-1

bounded sequence from above

if there is some number M such that a_n </= M, M is called “upper bound”

bounded sequence from below

if there is some number m such that a_n >/= m, m is “lower bound”

monotonic sequence

if {a_n} is increasing for all n (ex: a_n < a_n+1)

if (a_n} is decreasing for all n (ex: a_n > a_n+1)

monotonic sequences converges

if {a_n} is monotonic increasing and a_n < M, then {a_n} converges

if {a_n} is monotonic decreasing and a_n >/= m, then {a_n} converges

convergence of infinite series

an infinite series converges to the sum S if the sequence produced by its partial sums {S_N} converges to S

geometric series

a_n = crⁿ

c₁r does not equal 0

partial sums = [c(1-r^N-1)] / [1-r]

nth term divergence test

if limit of a_n as n approaches infinity doesn’t equal 0, then sum of a_n from n = 1 to infinity diverges

positive series

sum of a_n where a_n > 0

if the partial sums S_N are bounded above, then a_n converges

if the partial sums S_N are not bounded above, then a_n diverges

integral test

a_n = f(n) - positive, decreasing, continuous function of x when x>/= 1

if integral of 1→infinity f(x)dx converges, so does series

if integral of 1→infinity f(x)dx diverges, so does series

p-series convergence

if p > 1 in sum of 1/n^p , the series converges

direct comparison test

assume there exists M > 0 such that 0 </= a_n </= b_n for all values of n greater than or equal to M

if b_n converges, a_n also converges

if b_n diverges, a_n also diverges

limit comparison test

let a_n and b_n be 2 positive sequences such that lim of n→infinity of a_n / b_n = L

if L > 0, then a_n converges if and only if b_n converges

if L = infinity, if a_n converges, b_n converges

if L = 0, if b_n converges, a_n converges

alternating series

terms alternate from positive to negative

(-1)^n-1 a_n or (-1)ⁿ

always converges

converges conditionally if a_n = 1/n (harmonic)

absolute convergence

if |a_n| converges

implies a_n converges

conditional convergence

if a_n converges but not |a_n|

ratio test

assume that the following limit exists

P = lim n→infinity | (a_n+1) / a_n |

if P<1 a_n converges absolutely

if P>1, a_n diverges

if P=1, the test is inconclusive

root test

assume the following limit exists: L = lim n→infinity ⁿ√|a_n|

if L<1, converges absolutely

if L>1, diverges

if L=1, inconclusive

power series

sum of n=0 to infinity of a_n(x-c)ⁿ

converges if |x-c|<R

diverges if |x-c|>R

taylor polynomials

approximations of functions as polynomials that “agree” with the function at a point and that point’s first n derivative (rate of change/slope)

T_N (x) = f(c) + [f’(c)/1!](x-c) + [f’’(c)/2!](x-c)²+…+[f^N(c)/N!](x-c)^N

maclourin series

a Taylor series that is centered at 0