Set Theory

T/F - The following equation is valid:

Given A = {1, 2, 3}; B = {1, 2}

A + B = {1, 1, 2, 2, 3}

False

Sets can only use union, intersection, and complement operations

universal set

largest available set/container

write a set, U, with points “1, 2, 3”

U = {1, 2, 3}

set union

all elements in and between sets

set intersection

all elements shared between sets

set complements

all elements NOT in a set (includes those in universal set)

Write “union between A and B” symbolically

A U B

Write “intersection between A and B” symbolically

A ∩ B

Write “complement of A” symbolically

A^C

Write “A has no elements” symbolically

A = Ø

T/F - The intersection of A = {1, 2} and B = {3, 4} is 0

False
A ∩ B = Ø

Given the following, find A^C U B

U = {1, 2, 3, 4, 5}

A = {1, 2, 3}

B = {1, 3, 5}

A^C U B = {1, 3, 4, 5}

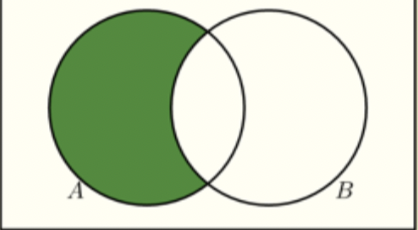
Write the set symbolically

A ∩ B^C

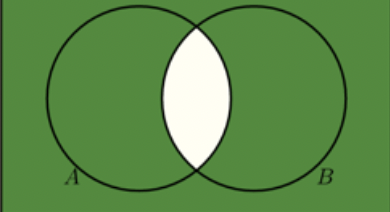
Write the set symbollically

(A ∩ B)^C OR (A^C U B^C)

De Morgan’s Rule

Union and Intersections are complements of each other such that
(A ∩ B)^C = (A^C U B^C)

(A U B)^C = (A^C ∩ B^C)

sample space

collection of all possible outcomes of an experience

What are all the possible outcomes for rolling a die twice (use shorthand)

S = {11, 12, …, 16

21, 22, …, 26

⋮

61, 62, …, 66}

event

any subset of a samplespace

Write “A is a subset of B” symbolically

A ⊆ B

differentiate subsets from mutually exclusive events

• subsets are sets where A = (A ∩ B) [all elements in one are in the other]

• mutually exclusive events describe sets where (A ∩ B) = Ø [no intersection between sets]

Given the following sample space, find the subset

S = {11, 12, …, 16

21, 22, …, 26

⋮

61, 62, …, 66}

E = {xy ∈ S: x = y/2}

E = {12, 24, 36}

Given the following sample space, find the subset

S = {11, 12, …, 16

21, 22, …, 26

⋮

61, 62, …, 66}

E = {xy ∈ S: x + 2 < y}

E = {14, 15, 16, 25, 26, 36}

Write the total number of elements in the set symbolically

S = {11, 12, …, 16

21, 22, …, 26

⋮

61, 62, …, 66}

|S| = 36

T/F - A ⊆ B

A = { 1, 2, 3}

B = { 3, 3, 3}

True

Duplicates are considered the same element