Set Theory

set

a collection of objs called ELEMENTS

• the elements do not have to be of the same “type”

• 1 ∈ A if 1 is an element of set A

two sets are EQUAL if they:

contain the same elements no matter the order or multiplicity (ex. one set may have one 2 and the other set may have two 2’s)

sets can be:

• a simple list of elements

• a description of the elements that are included in the set (ex. A = {3n | n ∈ Z, 1 ≤ n ≤ 12} = {3, 6, 9, ..., 36})

commonb sets in math

set of: natural numbers (N), integers (Z), rational numbers (Q), real numbers (R), positive integers (Z+), negative integers (Z-)

empty set

• denoted ∅ or {} BUT NOT {∅}

• contains NO elements

universal set

• denoted “U”

• set of all elements that are ANALYZED (not every element that could exist, although it could mean that)

subset

let A and B be two sets.

• A is a subset of B (A ⊆ B) if all the elements of A are also elements of B (A is CONTAINED in B), A could also = B)

• if A is a subset of B, then for all x ∈ U, the implication (x ∈ A) → (x ∈ B) is true (if x is an element of A, then it must be true that x is an element of B)

if X is a set, then

∅ (empty set) ⊆ X is a tautology since:

• (F → (x ∈ X)) is a tautology (think back to the IMPLICATION definition of a subset)

proper subset

let A and B be sets.

• A is a proper subset of B if A ⊆ B and A ̸= B. If so, we write A ⊂ B.

• or, A is a subset of B AND A ≠ B

cardinality

if A is a set containing EXACTLY n DISTIINCT (do not count duplicates of elements) elements (where n ≥ 0), then A is a FINITE set and its “cardinality” is n.

• denote the cardinality of A by |A|. (here, |A| = n)

power set

• denoted P(A)

• set of ALL distinct subsets of A

• P(A) = {X | X ⊆ A}

cardinality of a power set

let A be a set

• if |A| = n, then |P(A)| = 2^n

cartesian product

let A and B be sets.

• the cartesian product of A and B, denoted by A × B, is the set of all pairs (a, b) where a ∈ A and b ∈ B (so, rmbr that the cartesian product is a SET)

• A × B = {(a, b) | a ∈ A, b ∈ B}

cardinality of a cartesian product

• let A x B be a cartesian product

• |A × B| = |A||B| → cardinality of A × B is equal to the PRODUCT of the cardinalities of A and B.

properties of a cartesian product

• NOT commutative: A × B = B × A. is generally false

• NOT associative: (A × B) × C = A × (B × C) is generally false

let A1, A2, ..., An be sets. the cartesian product A1 × A2 × ... × An is the set:

A1 × A2 × ... × An = {(a1, a2, ..., an) | ai ∈ Ai, 1 ≤ i ≤ n}

• denoted by A^n

• think of a squared factor like (x - 2)²

• ex. let B = {1, 2, 3}, B³ = {(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)}

• ex. R³ = {(x, y, z) | x, y, z ∈ R} = R x R x R = every 3D point that exists in R³

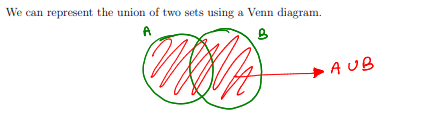
let A, B be two diff sets, the union of A and B:

• A ∪ B = a set that contains every element in A OR B

• A ∪ B = {x | (x ∈ A) ∨ (x ∈ B)} → for every element x, the set A ∪ B is where x belongs to EITHER A OR B)

• see image for diagram

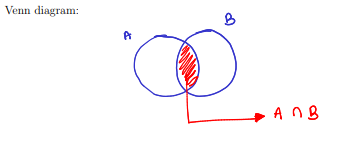
let A, B be two diff sets, the intersection of A and B:

• A ∩ B = the set of all elements that belong to A AND B

• A ∩ B = {x | (x ∈ A) ∧ (x ∈ B)}

sets A and B are DISJOINT if:

• they share no similar elements

• in other words, the set A ∩ B = ∅

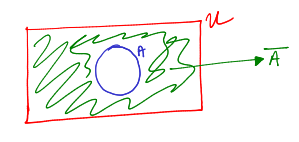
complement of a set

• the complement of a set A is denoted A’

• A’ = {x | x ∈ U ∧ (x /∈ A)} → every element in “universe” that doesn’t belong to A is in the complement set

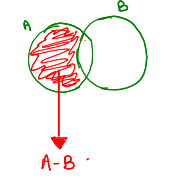
let A, B be two diff sets, the difference of A and B:

• denoted as A - B (B - A would be a completely diff set)

• A - B = {x | (x ∈ A) ∧ (x /∈ B)} → set of every element that belongs to A and DOESN’T belong to B

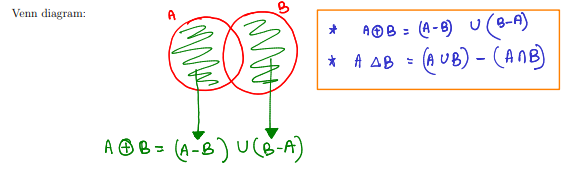
let A, B be two diff sets, the SYMMETRIC difference of A and B:

• denoted as A ⊕ B

• A ⊕ B = {x | (x ∈ A) ⊕ (x ∈ B)} → set of all elements that either in A or in B, but not both

• A ⊕ B = (A - B) U (B - A) → symmetric difference aspect

set identities

see lecture notes 9

• incorporate proof strats

• rmbr the mathematical definitions of unions, intersections, subsets, etc

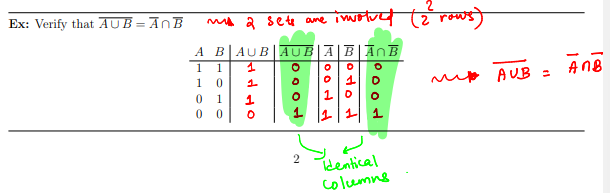
membership table

• used to verify set identities

• almost the same as a truth table

• if n sets are contained in identity, then the num of rows = 2^n (same as truth table w proposition variables)

• for a set A, truth value of 1 means x belongs to A, and 0 means x does not belong to A

• recall that two things are logically equivalent (equal to each other) if they have the same truth values (←> “if and only if” is a tautology)