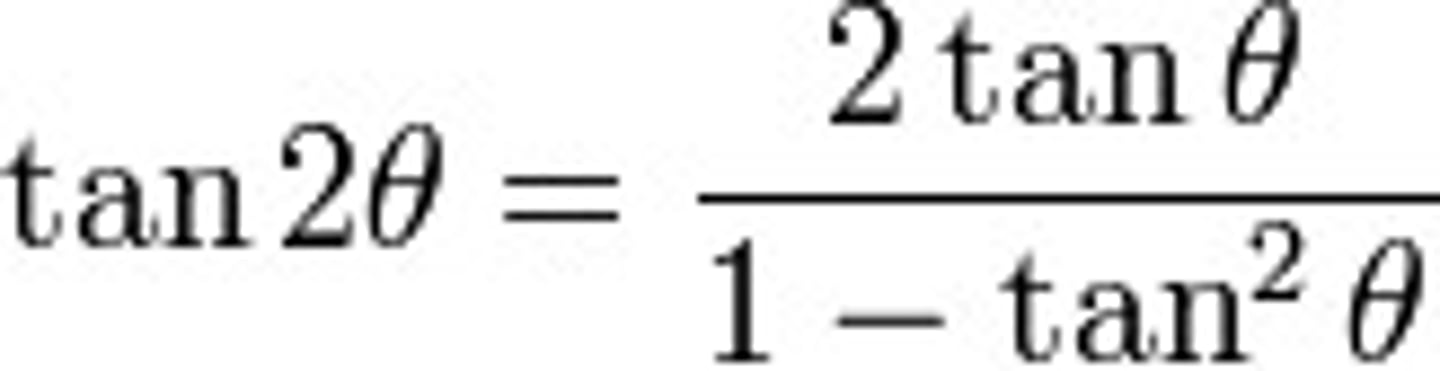AP Precalculus - Trig Identities
1/31
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
32 Terms
Reciprocal identity of sinx
sinx = 1/cscx
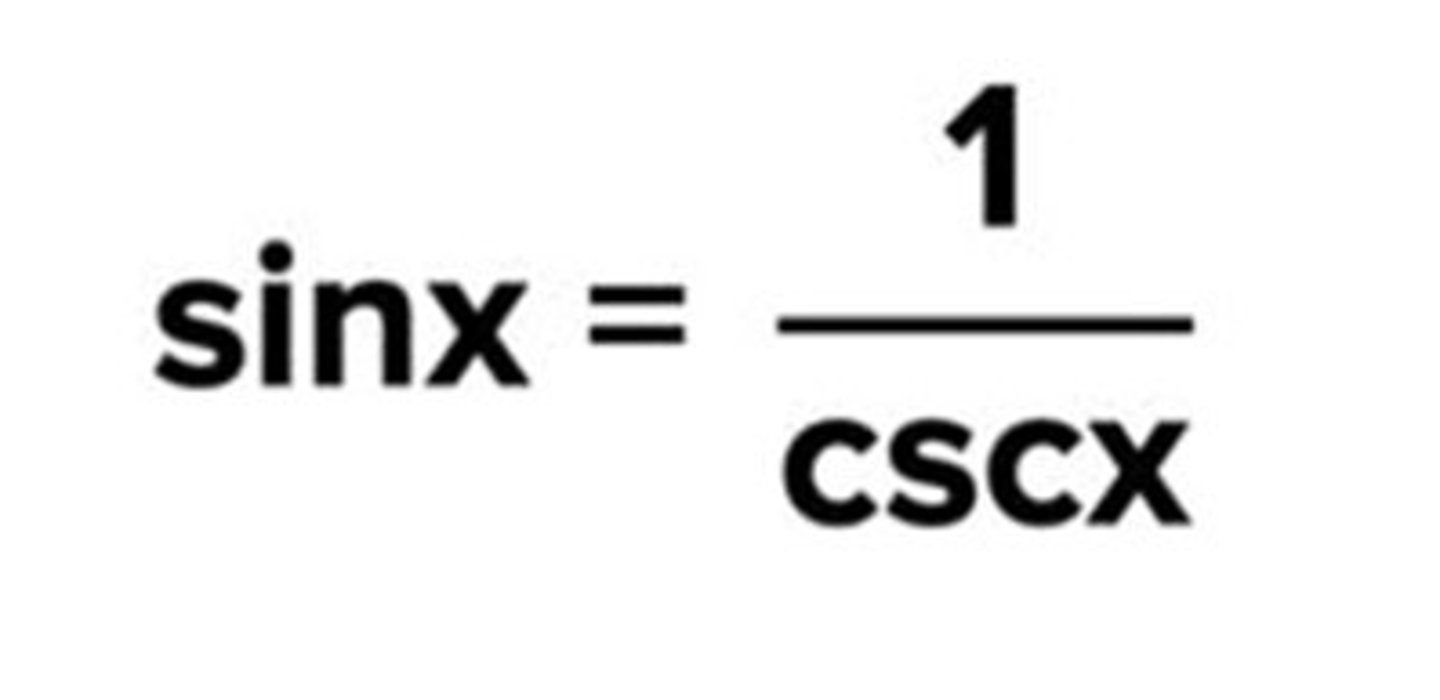
Reciprocal identity of cosx
cosx = 1/secx
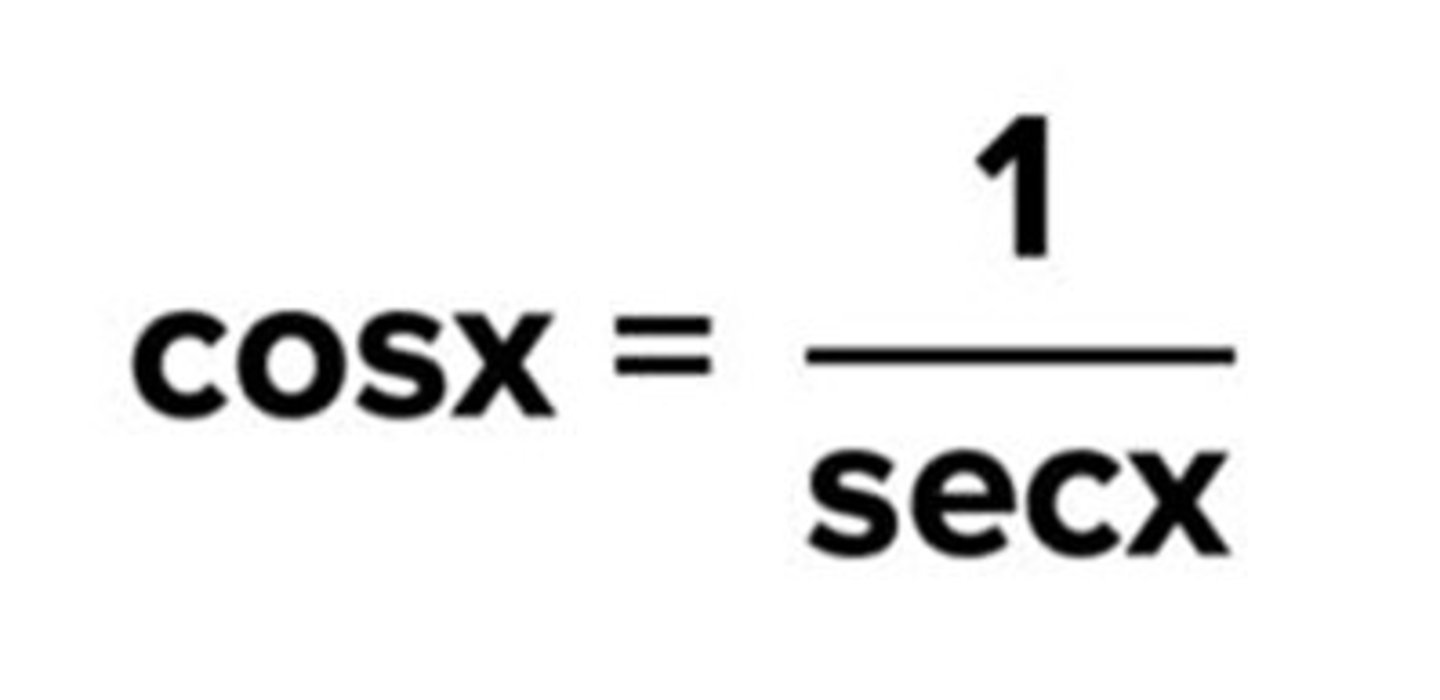
Reciprocal identity of tanx
tanx = 1/cotx
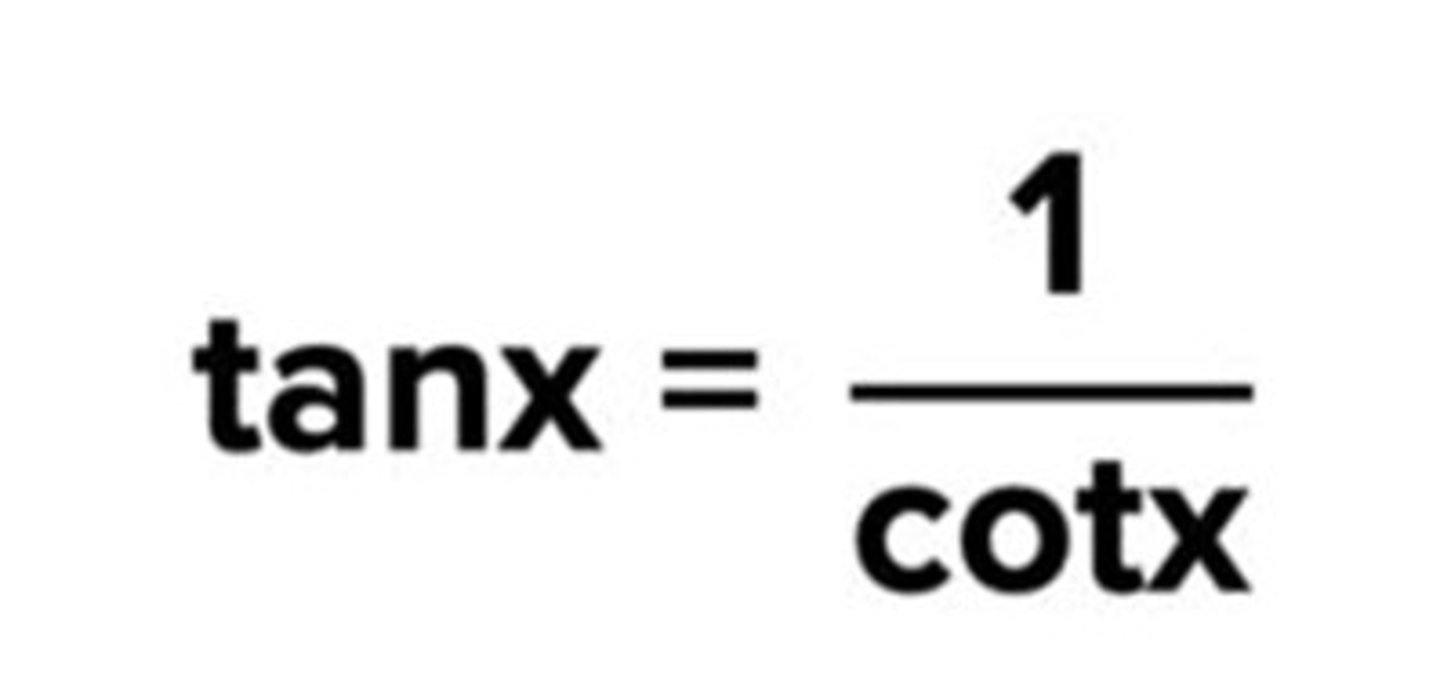
Reciprocal identity of cscx
cscx = 1/sinx
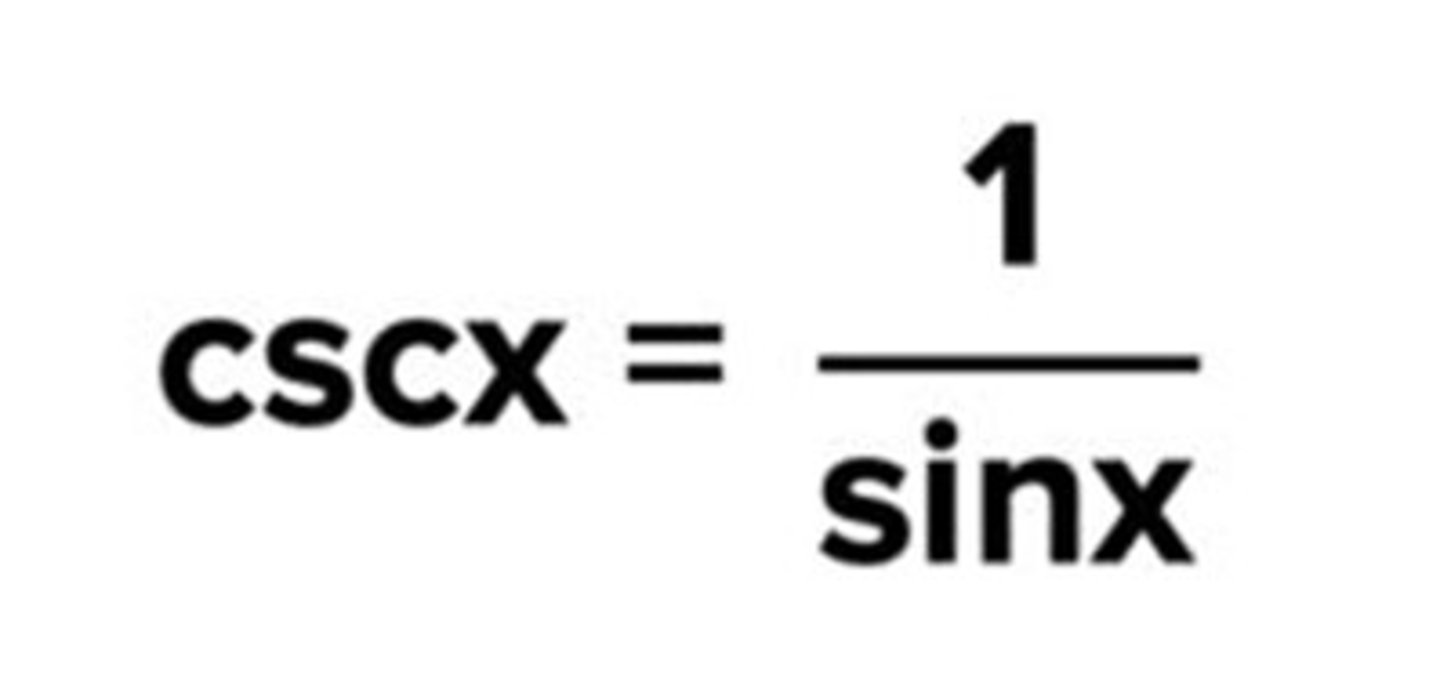
Reciprocal identity of secx
secx = 1/cosx
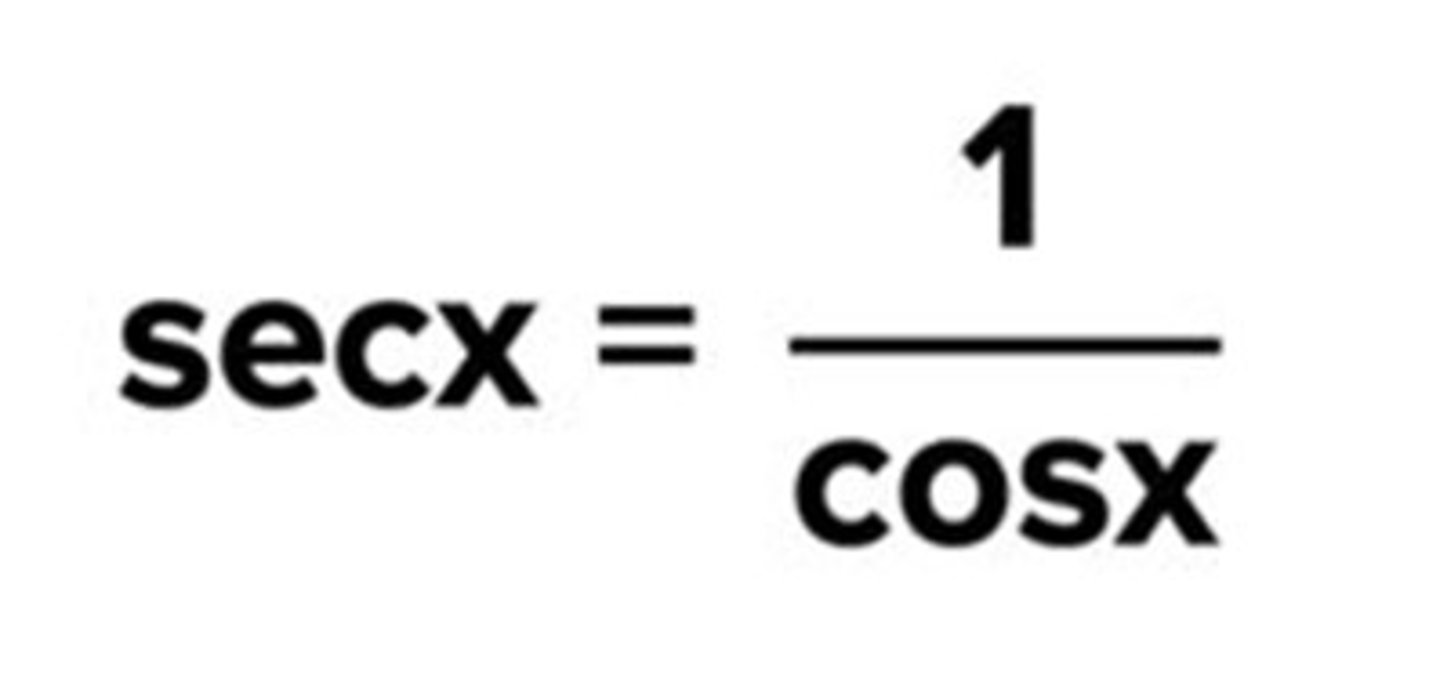
Reciprocal identity of cotx
cotx = 1/tanx
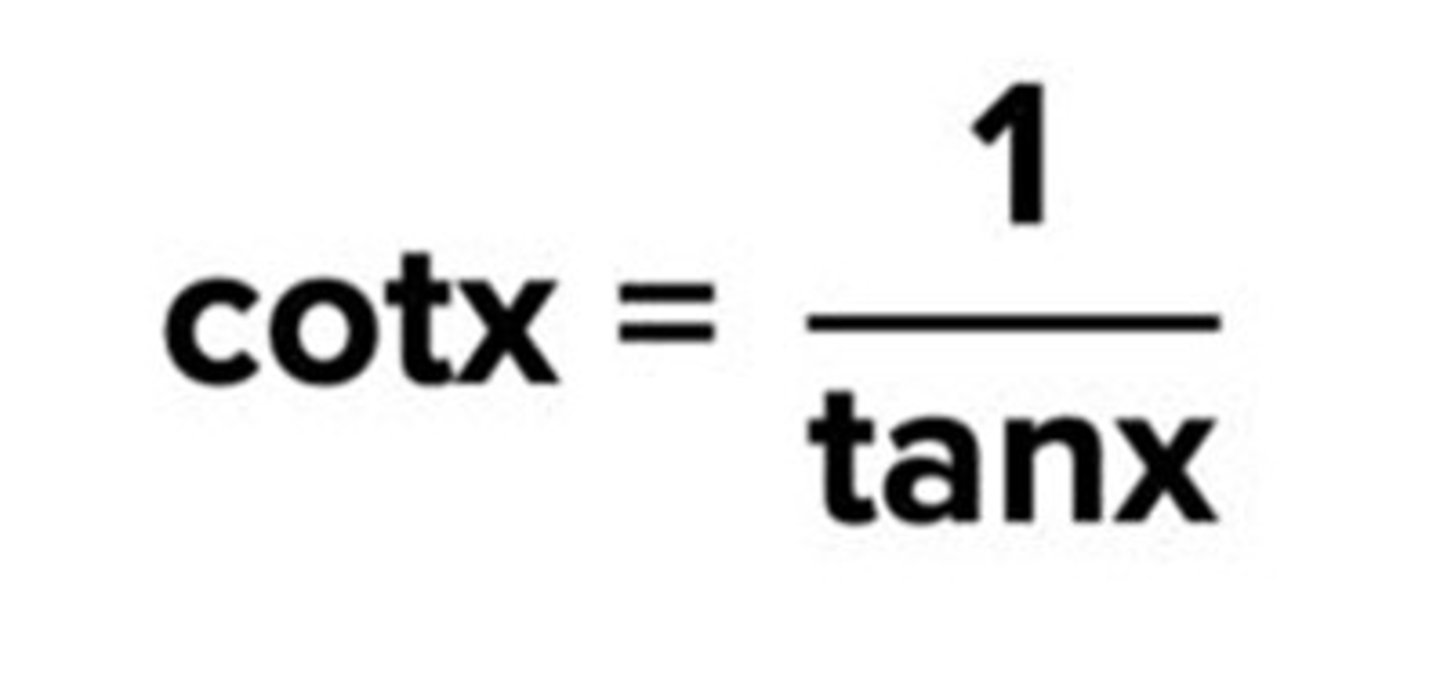
Quotient identity of tanx
tanx = sinx/cosx
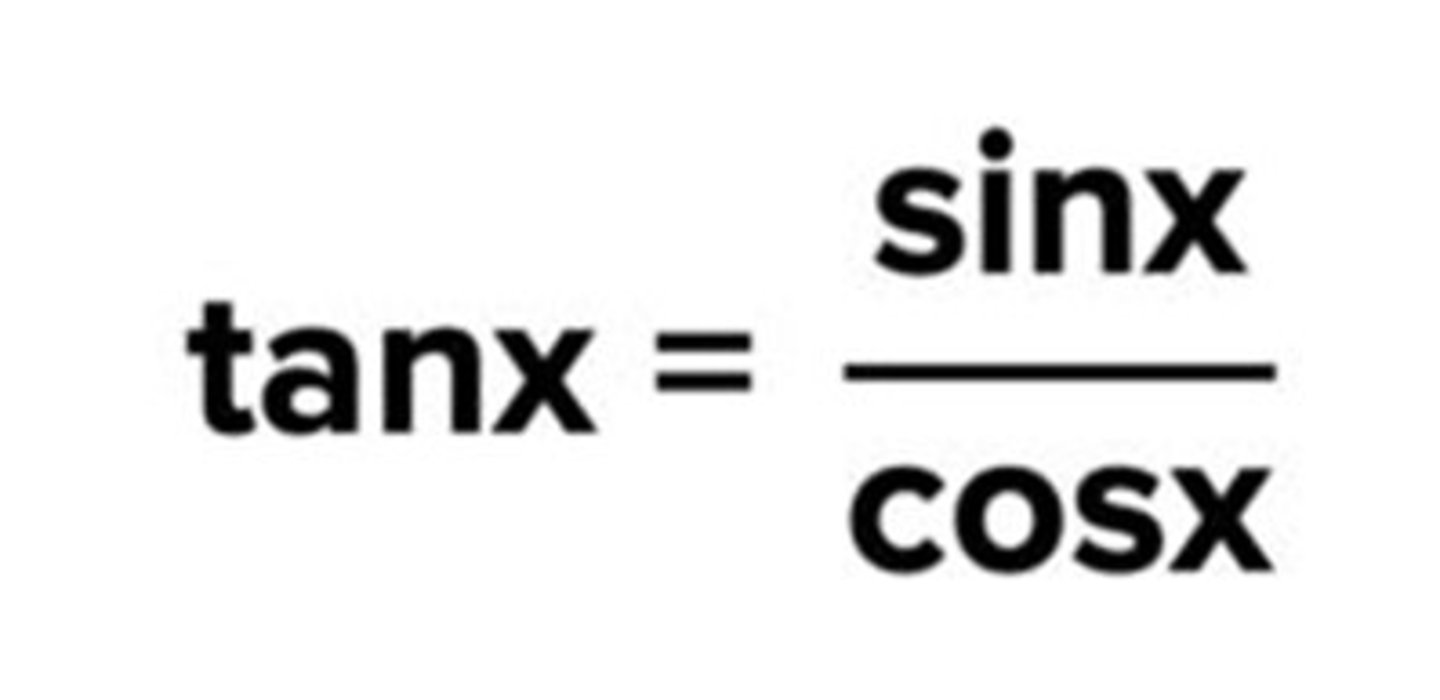
Quotient identity of cotx
cotx = cosx/sinx
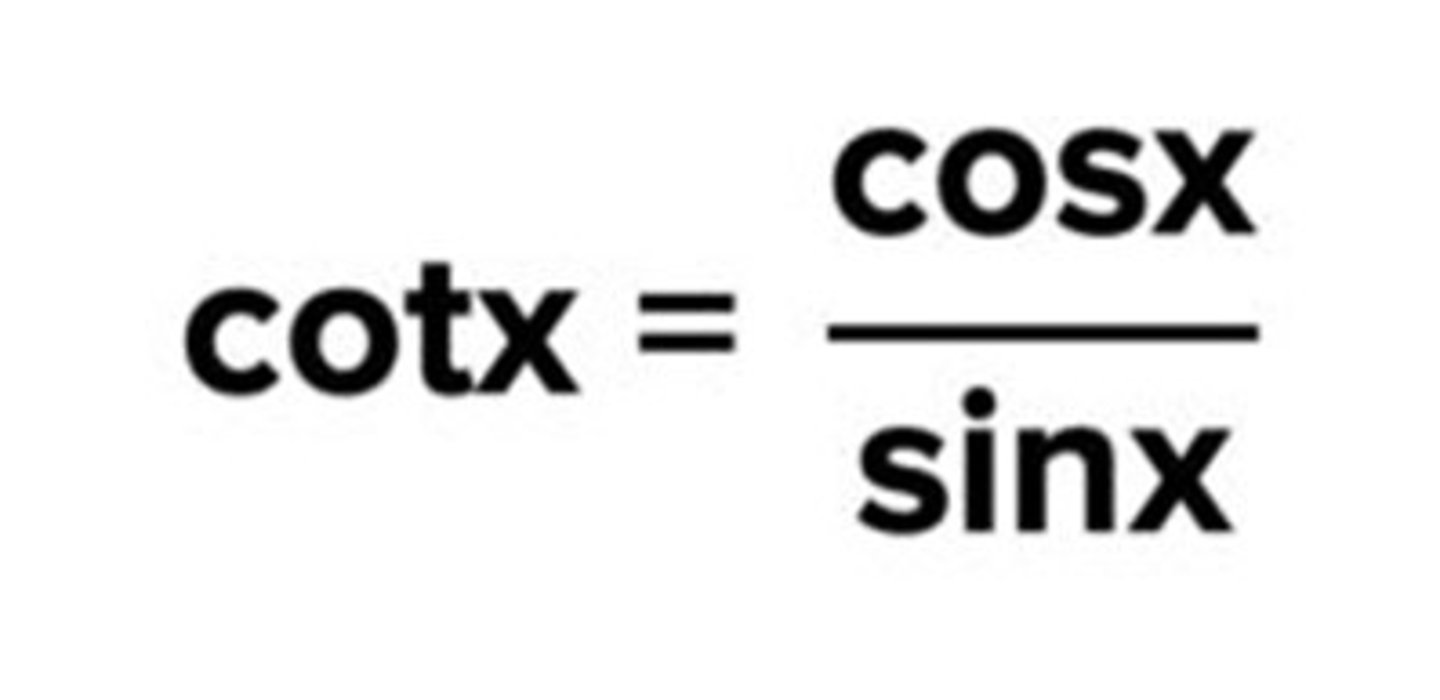
Pythagorean identity of sin and cos
sin²x + cos²x = 1
cos²x = 1 - sin²x
sin²x = 1 - cos²x
cos²x + 1 = -sin²x
sin²x + 1 = -cos²x
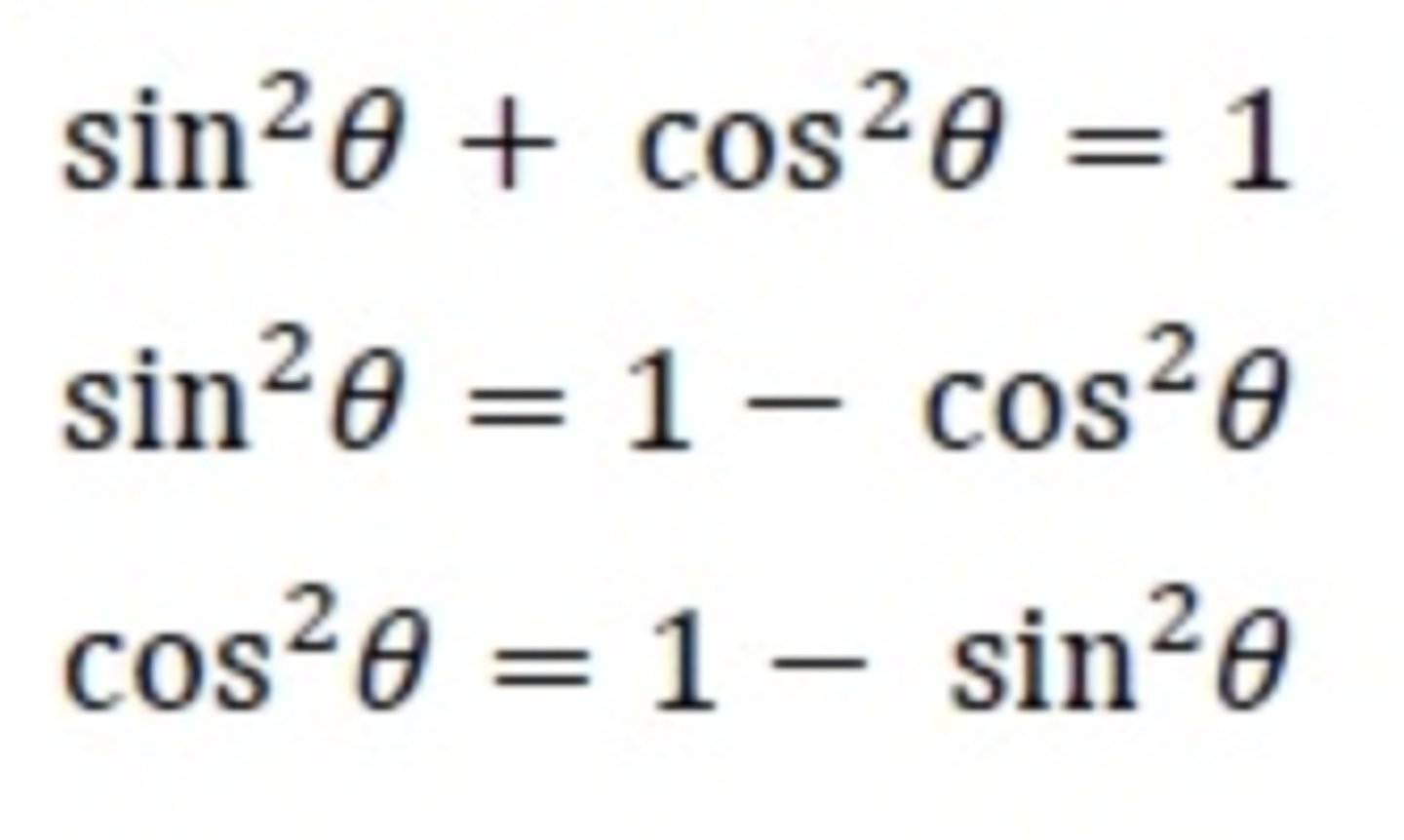
Pythagorean identity of tan and sec
1 + tan²x = sec²x
tan²x = sec²x - 1
1 = sec²x - tan²x
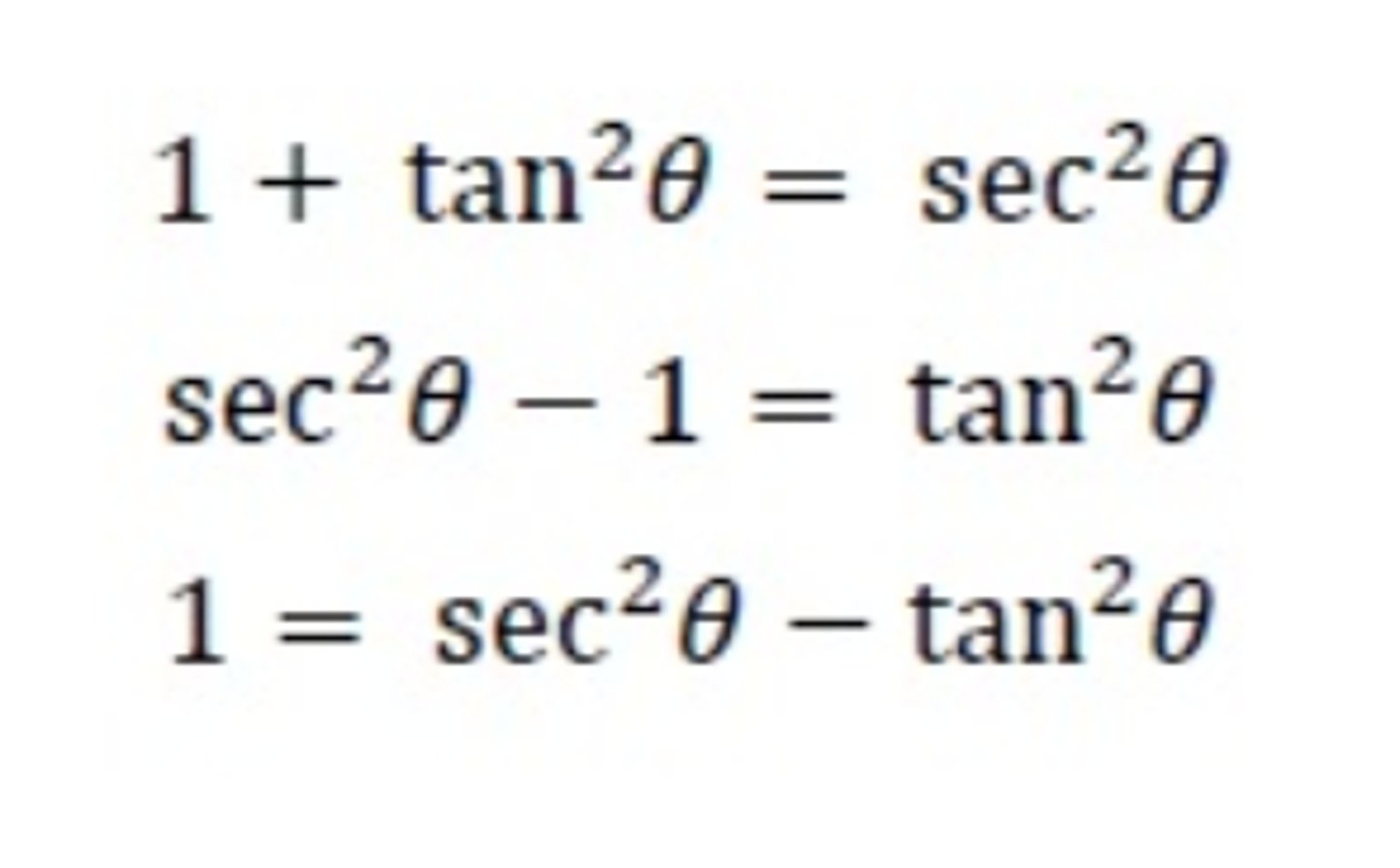
Pythagorean identity of cot and csc
1 + cot²x = csc²x
cot²x = csc²x - 1
1 = csc²x - cot²x
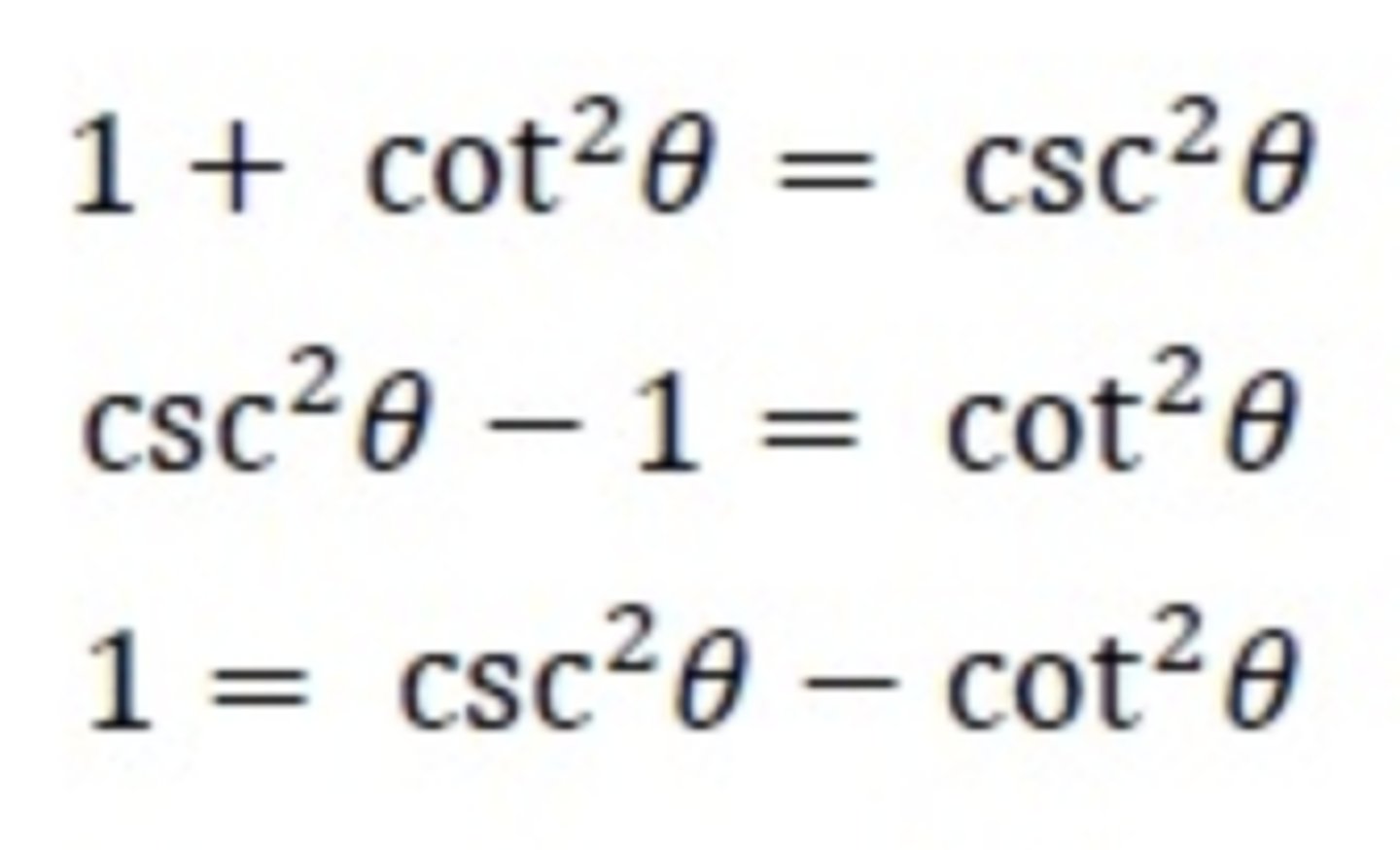
Cofunction identity of sin
sin(π/2 - x) = cosx
Cofunction identity of cos
cos(π/2 - x) = sinx
Cofunction identity of tan
tan(π/2 - x) = cotx
Cofunction identity of cot
cot(π/2 - x) = tanx
Cofunction identity of sec
sec(π/2 - x) = cscx
Cofunction identity of csc
csc(π/2 - x) = secx
Odd identity of sin
sin(-x) = -sinx
Odd identity of csc
csc(-x) = -cscx
Even identity of cos
cos(-x) = cosx
Even identity of sec
sec(-x) = secx
Odd identity of tan
tan(-x) = -tanx
Odd identity of cot
cot(-x) = -cotx
Sum formula for sine
sin(u + v) = sin(u)cos(v) + cos(u)sin(v)
Difference formula for sine
sin(u - v) = sin(u)cos(v) - cos(u)sin(v)
Sum formula for cosine
cos(u + v) = cos(u)cos(v) - sin(u)sin(v)
Difference formula for cosine
cos(u - v) = cos(u)cos(v) + sin(u)sin(v)
Sum formula for tangent
tan(u + v) = (tan(u) + tan(v)) / (1 - tan(u)tan(v))
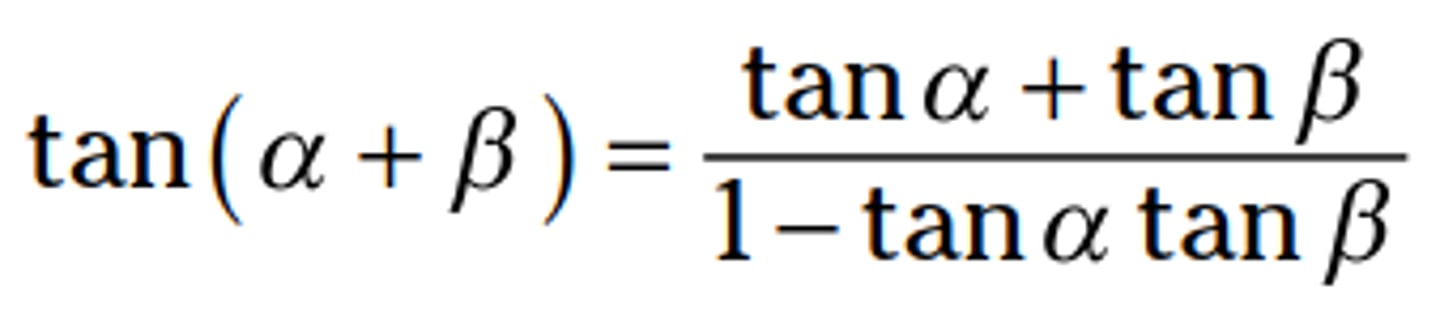
Difference formula for tangent
tan(u - v) = (tan(u) - tan(v)) / (1 + tan(u)tan(v))
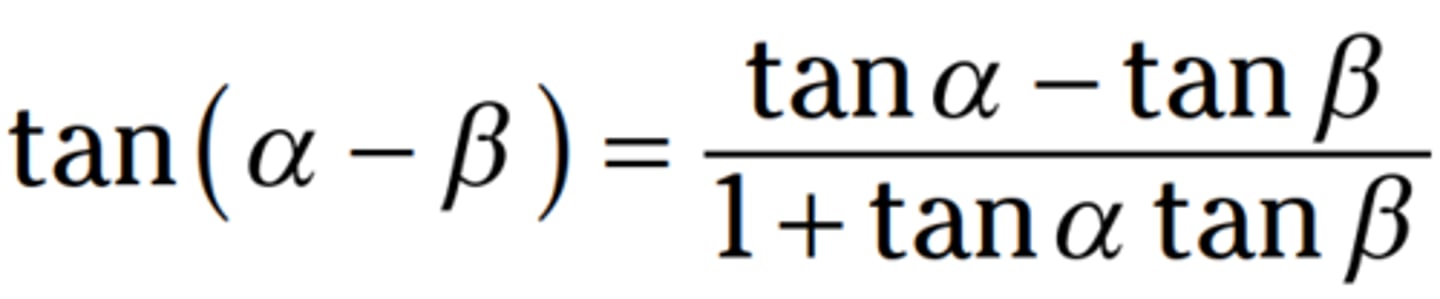
Double angle formula for sine
sin(2x) = 2sin(x)cos(x)
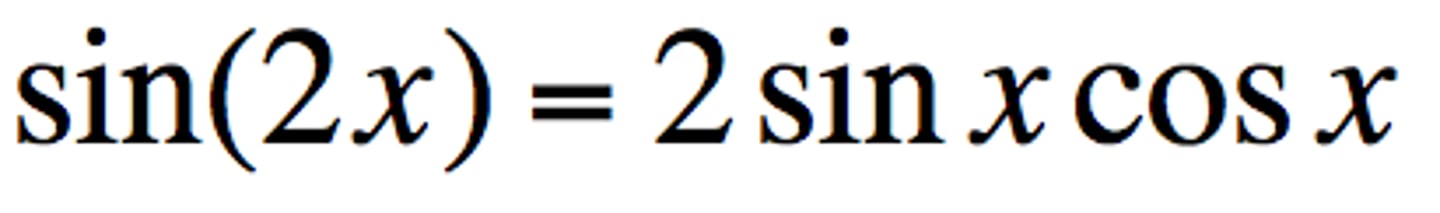
Double angle formula for cosine
cos(2x) = cos²x - sin²x
= 2cos²x - 1
= 1 - 2sin²x
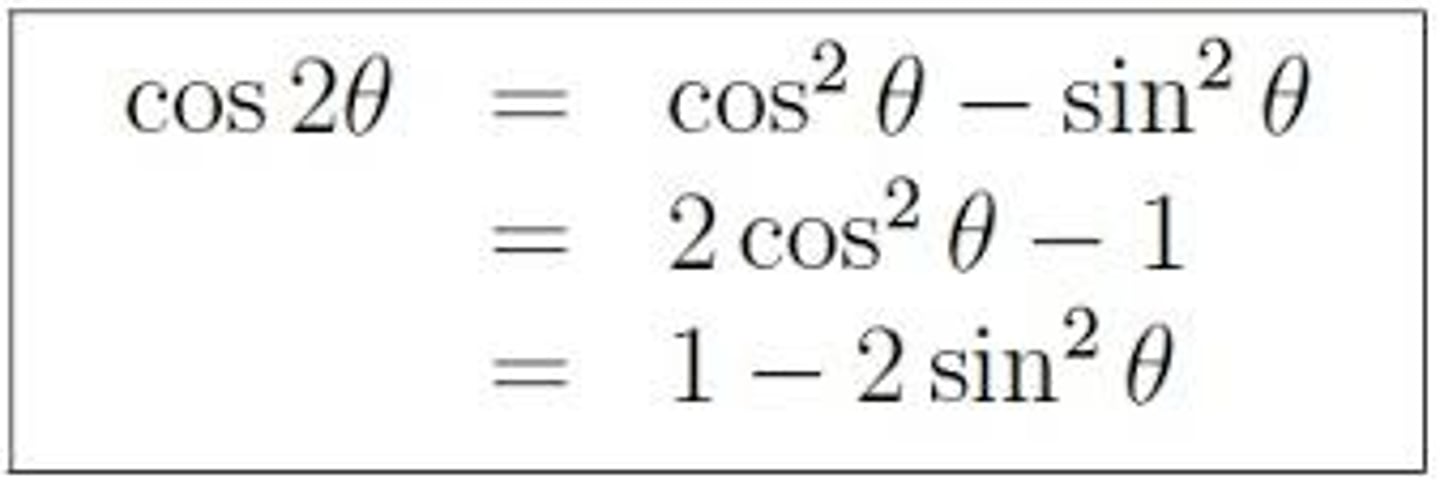
Double angle formula for tangent
tan(2x) = 2tan(x) / (1 - tan²x)