Calculus 1: Chapter 4 Test Review

Find the limit: lim x→∞ (1+a/x)^bx

1. Find derivative using Chain Rule/Quotient Rule

2. Apply L' Hospital Rule Once

3. Convert log back into e^ab

4. Final Answer: e^ab

Find the limit: lim x→∞ ((2x-3)/(2x+5)^2x+1

1. Convert [f(x)]^g(x) —> limx→∞ lny = limx→∞ g(x) ln[f(x)]

2. Apply L’Hospital Rule Once

3. Find derivative using Quotient Rule/Chain Rule 

4. Convert back limx→∞ lny = -8 

5. Final Answer: e^-8

How to determine where f is increasing or decreasing?

Take the first derivative ——→ f’(x) 

f’(x)>0 = increasing 

f’(x)<0 = decreasing 

How to determine where f is concave up or down?

Same as finding where f is inc/dec but just take f’’(x)

cosx=0 on?

x = π/2, 3π/2

sinx = -1 on?

x = 3π/2

How to determine inflection points?

1. Solve where f’’(x) = 0, Critical Numbers

2. Input numbers into f’’(x) before and after C.N to find where f"(x) changes from (+) to (-)/vise versa

Prove that limx→∞ (e^x)/(Xⁿ) = ∞

1. Use L’Hospital Rule 

2. Derivative of e^x stays e^x

3. Derivative of Xⁿ becomes nx^n-1 (a constant) 

4. It will always be ∞

Prove that limx-∞ (lnx)/(X^p) for any p>0

1. Use L’Hospital Rule

2. Derivative of lnx = 1/x

3. Derivative of X^p is px^p-1

4. Limit becomes 1/px^p1 

5. If p>0, then X^p will approach ∞

6. Basically 1/∞ = 0

If an initial amount A₀ of money is invested at an interest rate r compounded n times a year, the value of the investment after t years is

A(t) = A₀ (1 + r/n)^nt

If we let n→∞ it represents continuous compounding: A(t) = A₀ e^rt

Show that A(t) = A₀ (1 + r/n)^nt can equal to A(t) = A₀ e^rt if n approaches infinity.

1. Convert [f(x)]^g(x) —> limx→∞ lny = limx→∞ g(x) ln[f(x)]

2. Apply L’Hospital Rule

   1. Use chain rule: g’[h(x)] h’

   2. Factor out n

3. Convert log back

4. Final answer: A₀e^rt

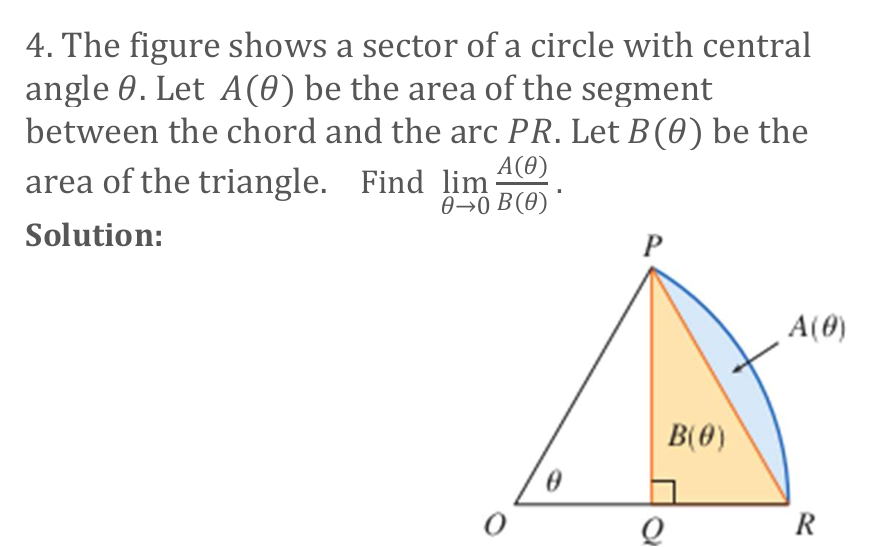
1. Find the area of Bθ 

   1. Base = 2sinθ

   2. Triangle Area: ½ (base)(height)

   3. Plug numbers into area of a triangle

2. Since r=1… B(θ) = ½ sinθ

3. Find area of A(θ)

   1. Sector Area: ½ θ

   2. Sector Area: sector area - triangle area

4. Plug into Aθ/Bθ

5. Evaluate Limit

6. Final Answer: 0

1. Plug in values into limx→∞ g(x) ln[f(x)]

2. (∞) *( -∞) = -∞

3. Convert back to log

4. e^{^}-∞

5. Final Answer: 0^∞ always goes to 0 so NOT indeterminate

Use guidelines to sketch the curve

y = x / x² - 4

1. Find Domain by setting denominator to = 0

2. Find Y-int by plugging in 0

3. Find X-int by setting it = 0

4. Find where its inc/dec and local extremas

5. Find concavity

6. Use graphing calculator to make sure!!

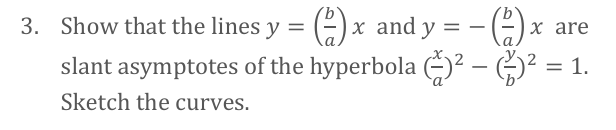
Horizontal Hyperbola: (x/a)² - (y/b)² = 1

1. Solve for y

   1. y = +- b * square root of ((x²/a²) - 1)

2. Find asymptotes by setting horizontal hyperbola to 0

3. Plug into calculator and use a = 3, b=2

4. Use graphing calculator to graph!!

1. Plug into limx→∞ [f(x) - x²] = 0 

2. Take limit

   1. 1/∞ = 0

3. Find x and y intercepts

4. Use graphing calculator to confirm!

1. Perimeter constraint 

   1. x + 3x + 2h = 1200

   2. 4x + 2h = 1200

2. Solve for h

3. Area formula for trapezoid: A = ½ (b₁ + b₂)(h)

4. Take derivative

5. Set =0

6. Final Answer: Area is 90000 ft²

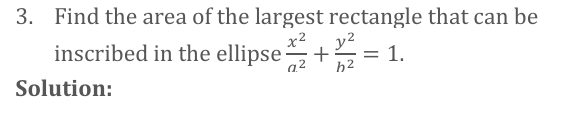
1. Solve ellipse for y 

2. Plug into area: A = 4xy 

3. Take Derivative

4. Find max area 

5. Final Answer: A_max = 2ab 

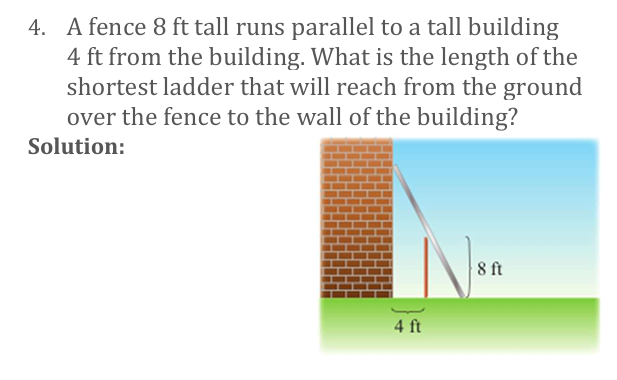
1. Using similar triangles

   1. Ladder length squared: L² = (x+4)² + (8(x+4)/x)²

2. Minimize this and derivative gives x=4

3. X = 4, then L = 16 ft

4. Final Answer: L = 16 ft

1. Average cost: c(x) = C(x)/x 

2. To minimize average cost, Take derivative 

3. set = 0 

4. Solve