Pure maths key facts (AS)

A tangent to a circle is…

Perpendicular to the radius

An angle inscribed in a semicircle is a…

Right angle/90°

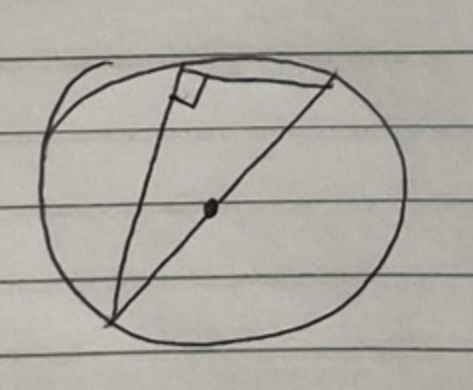
How do you go about proving that an angle is 90°?

You could look at the gradients of the two lines that meet to create the 90° angle.
Perpendicular lines' gradients multiply to give -1.

A perpendicular bisector of a chord…

Passes through the centre of the circle

Two perpendicular bisectors of a chord…

Meet at the centre of the circle

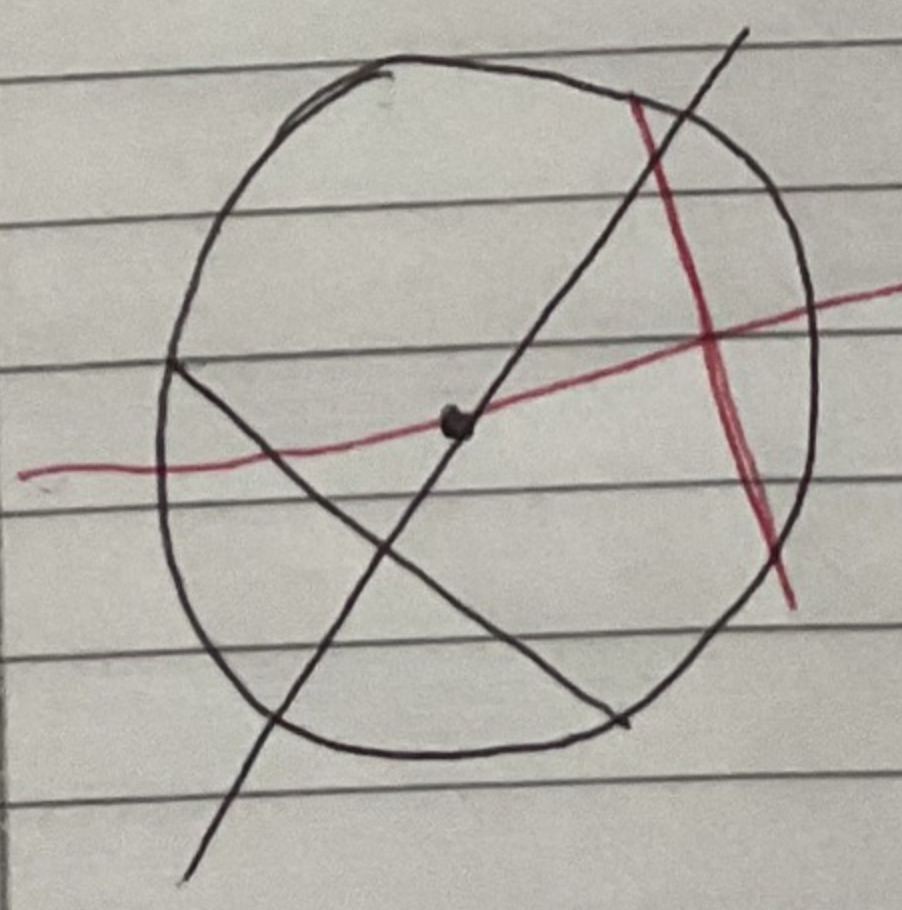
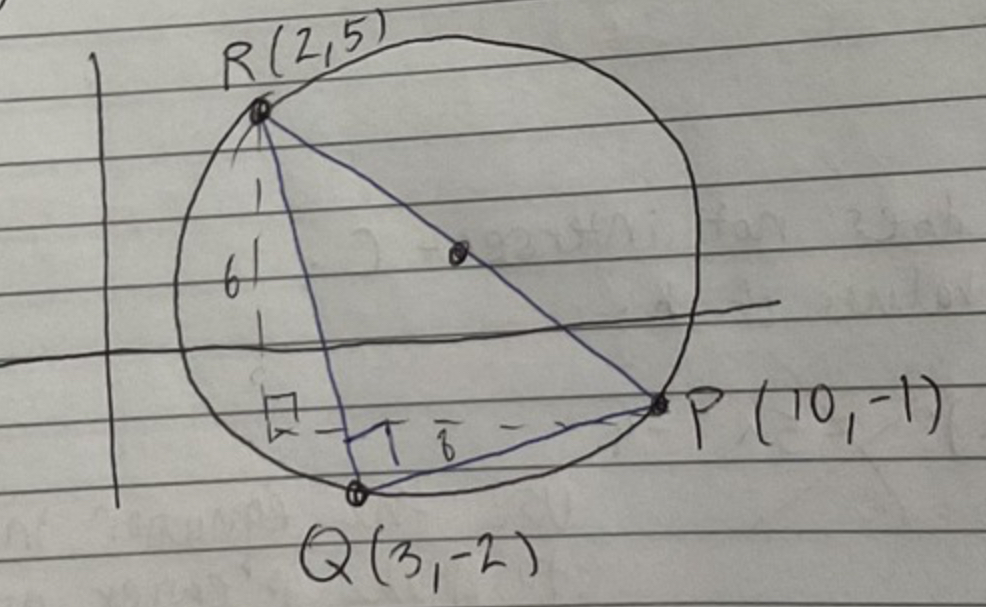
Equation of a circle

(x-h)²+(y-k)²=r²

What two things do you need to find the equation of a circle?

1. Coordinates of the centre
2. Length of the radius

How do you find the length of a line on the circle (e.g. the diameter, radius, a chord, etc), given two points?

1. Draw on a right-angle triangle that connects the two points
2. Find the difference between the y values and x values to find the length of a and b
3. Find c using Pythagoras
4. Square root c
   Note: if finding a radius, make sure to half the final value.

Chapter 7

Chapter 7

When finding the remainder, what do you do? Example equation = x³ + 10x² + 5 / x + 2

1. In the final box, there is -48 left.
2. You take away 5 from -48.
3. 5- -48 = 53. The remainder is 53.
4. Remember: original final number - final number in the box

if f(p) = 0, then…

(x-p) is a factor of f(x)

When using the factor theorem, you must state…what?

"…Hence, by the factor theorem"

When proving that something is divisible using the factor theorem, you must say… (Example: prove that 2x… is divisible by (x-1))

"If divisible by (x-1), then f(1) will equal 0"

Chapter 7b

Chapter 7b

Proof by deduction

• Starting from known facts or definitions, then using logical steps to reach the desired conclusion.
• Example: using 2n for even numbers, 2n+1 for odd numbers

Proof by exhaustion

Breaking the statement into smaller cases and proving each case separately.

Disproof by Counterexample

Using an example to disprove a statement — basically, an incorrect example that doesn't fit the hypothesis.

When finishing a proof question, write:

Hence, (repeat the statement)

Exam tip

'do something' to get started - be it factorising, combining two fractions, expanding, etc.
Also consider using even and odd numbers.

Chapter 8

Chapter 8

n choose r

n!
———
r!(n-r)!

Chapter 9

Chapter 9

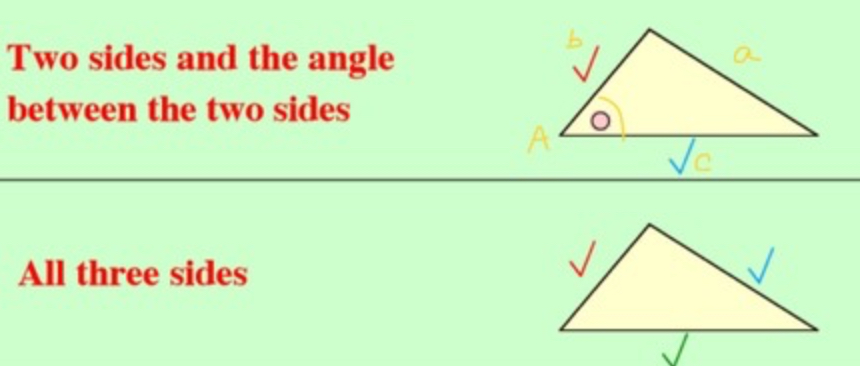
What is the cosine rule?

a² = b² + c² - 2bcCosA (for finding sides)

cos A = b² + c² - a² / 2bc (for finding angles)

When do you use the cosine rule?

• when you see an angle sandwiched between 2 known sides

• when you are given all three sides
  (No known opposites)

What is the sine rule?

a/sin A = b/sin B = c/sin C (for finding sides)

sin A/a = sin B/b = sin C/c (for finding angles)

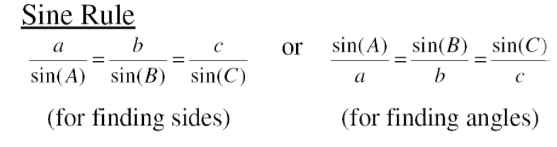
When do you use the sine rule?

• when given 2 sides and an angle
• when given 2 angles and a side
  One pair of opposites

Sine rule ambiguous case

When given that the angle is obtuse, you have to take away your found angle from 180°.

What is the sine rule for area?

Area = 1/2 abSinC

• when you see an angle sandwiched by both sides (no opposites)

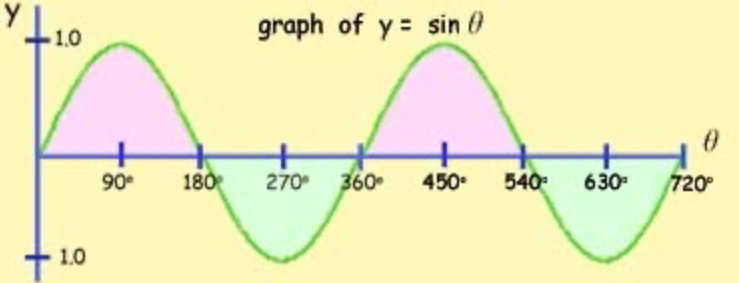
Sine graph

• sinx = sin(180-x)

• starts at 0

• crosses the x axis at = 0, 180, 360, 540

• repeats itself every 360° (positive and negative part)

• "leads" a cos graph by 90 degrees

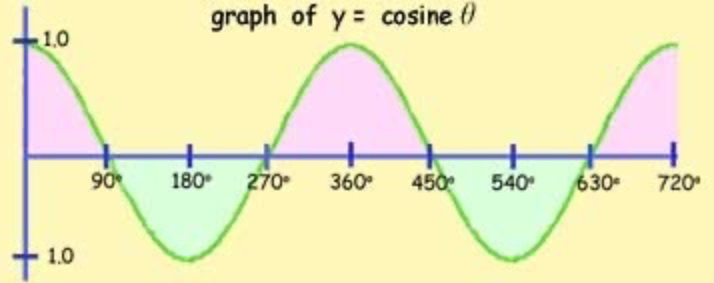
Cosine graph

• cosx = cos(360-x)

• starts at 1

• crosses the x axis at = -90, 90, 270, 450

• repeats itself every 360° (positive and negative part)

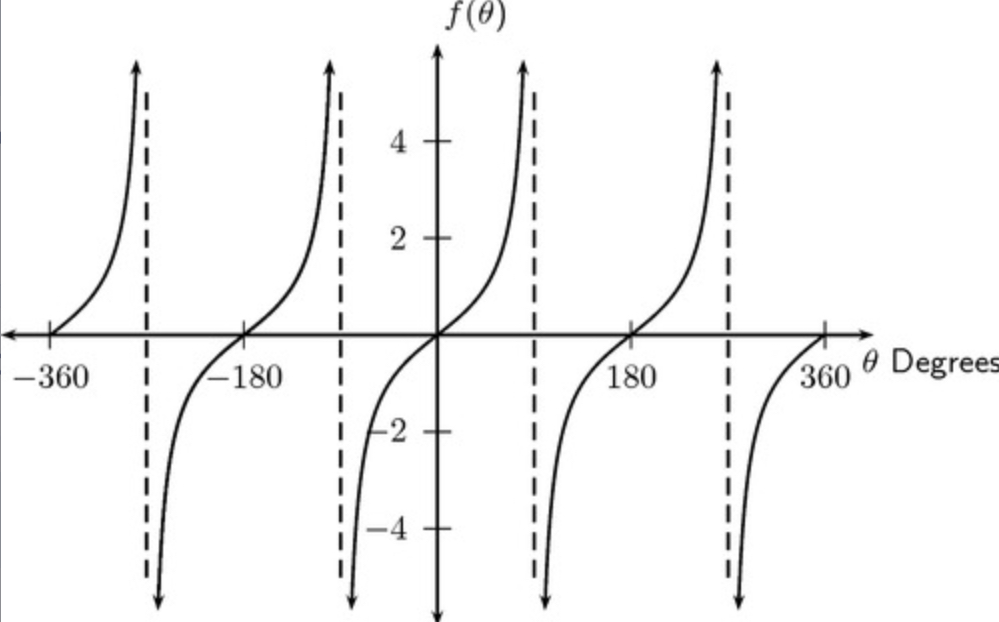
Tangent graph

• y=tanx
• repeats every 180°
• crosses the X axis at -180, 0, 180, 360
• no max + min values
• vertical asymptotes= -90, 90, 270

sin 0°

0

cos 0°

1

tan 0°

0

sin 90°

1

cos 90°

0

tan 90°

undefined

sin 45°

1/√2 or √2/2

cos 45°

1/√2 or √2/2

tan 45°

1

sin 30°

1/2

cos 30°

√3/2

tan 30°

1/√3 or √3/3

sin 60°

√3/2

cos 60°

1/2

tan 60°

√3

Chapter 10

Chapter 10

tanθ =

sin θ/cos θ

sin²θ+cos²θ=

1

The cosine function

sinθ = cos(90-θ)

cosθ = sin(90-θ)

Solving equations with sinθ

First, find the starting two angles: θ and (180-θ). Then add or subtract 360° as needed.

Solving equations with cosθ

First, find the starting two angles: θ and (360-θ). Then add or subtract 360° as needed.

Solving equations with tanθ

First, find the starting angle, θ. Then add or subtract 180° as needed.

Equations with linear inputs - expression inside the bracket

1. Change the range

2. Solve for new range first

3. Solve these answers for x/θ/etc.

4. If given a mixture of sin/cos/tan, then convert them into one thing and try to get just one of the three. (Example: divide sin(2x-20) by cos(2x-20) to get tan(2x-20)).

Chapter 11

Chapter 11

AB position vector

= AO + OB
= b - a

unit vector of a

(1/|a|)a

A unit vector in the direction of a = 3i + 4j

Magnitude = 5
Unit vector = 3/5i + 4/5j

Chapter 12

Chapter 12

Volume of a cylinder

V=πr²h

Volume of a sphere

4/3πr³

Volume of any prism

Area of cross section x length

Chapter 14

Chapter 14

Differentiate 3e^2x

6e^2x

What things do you need to think about when transforming an exponential graph?

SYA

• Shape
• y-intercept
• asymptotes