Biochem SI 5- Hemoglobin Allostery, Protein Methods, and Enzymes I/II

You are given the following data for the citrate → cis-aconitate reaction in a cell: [citrate] = 2.0 mM, [cis-aconitate] = 0.05 mM, ΔG°’ = +8.4 kJ/mol.

Calculate ΔG under these conditions (use RT = 2.48 kJ/mol at 25 °C) and state whether the reaction is favorable. Show your reasoning.

ΔG= ΔG°’+RT*ln([cis-aconitate]/[citrate])

ΔG= 8.4+2.48*ln(0.05/2)= -0.75 kJ/mol→ favorable b/c negative

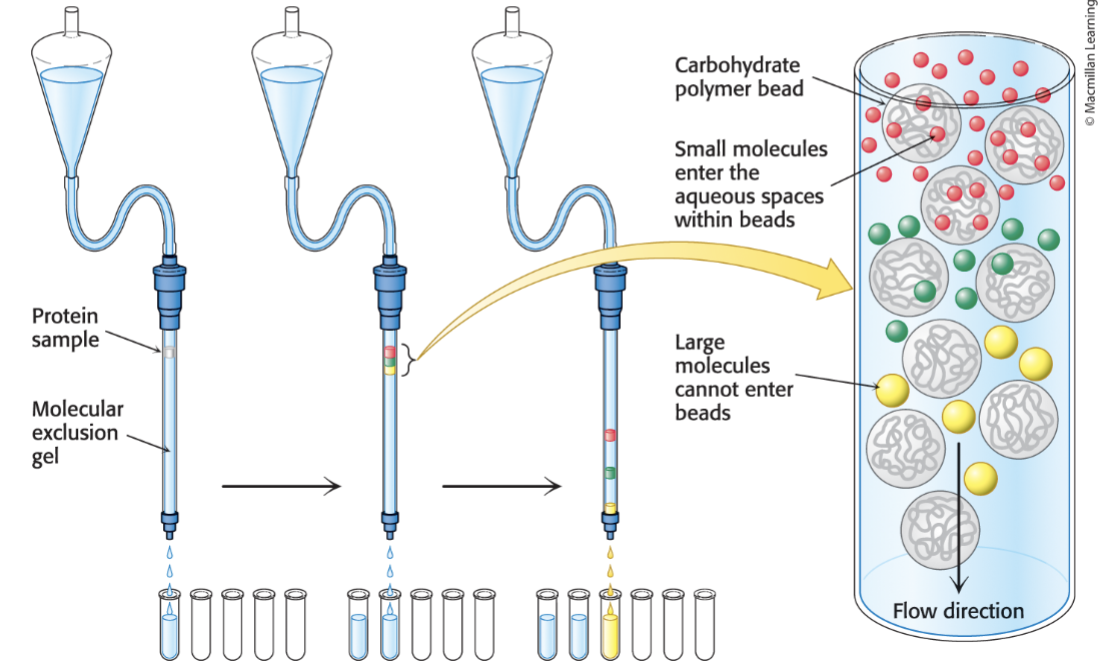
What is the principle of size-exclusion chromatography?

SEC separates molecules by size→ molecules are passed through a porous matrix.

Large molecules→ too large to enter the pores of the beads (matrix), so they move around and go through the column, so they elute first

Small molecules→ enter the pores of the beads (matrix), which slows their path. They elute later

Name one assay commonly used to detect enzyme activity during purification.

The presence of LDH (lactate dehydrogenase) can be detected by adding pyruvate and NADH to the mixture and measuring the absorbance at 340 nm over time→ NADH has absorbs light at 340 nm. This works because LDH catalyzes the conversion of NADH+pyruvate→lactate and NAD⁺. If LDH is present, it will consume NADH during the reaction, causing the absorbance at 340 nm to decrease steadily.

What does the diffraction pattern in x-ray crystallography represent?

The distribution of electrons/electron density in the protein→ aka its molecular structure

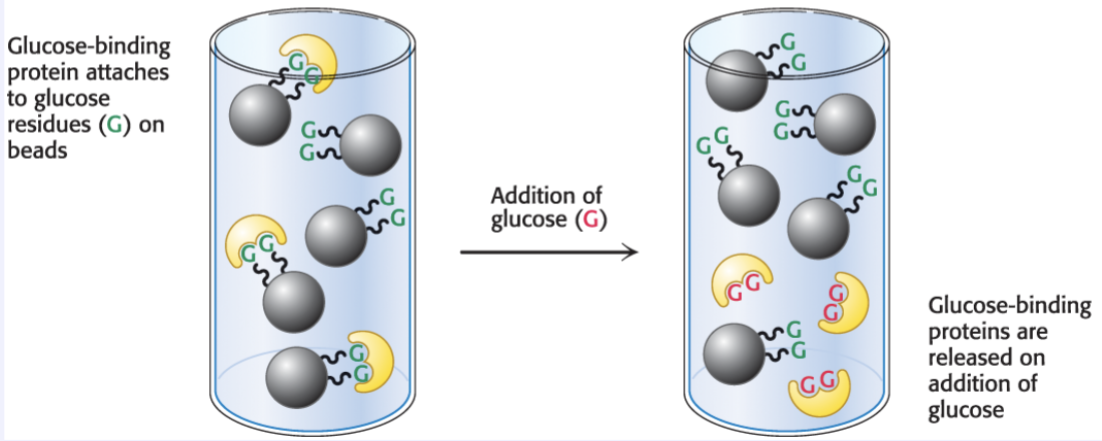
Compare ion-exchange chromatography and affinity chromatography in terms of what separates proteins.

Ion exchange→ Proteins are separated based on their charge and are placed in a charged matrix

• Anion exchange→ negatively charged proteins bind with positively charged beads

• Cation exchange→ positively charged proteins bind with negatively charged beads

Affinity→ Proteins are separated based on specific binding and are placed an a ligand-coated matrix

• Ligand binds only the target protein, and the unbound proteins wash away

• Target is eluted by adding a competing ligand or changing conditions to disrupt binding

Why must proteins usually be crystallized for x-ray diffraction studies?

In a crystal, all molecules are aligned in the same orientation, so the X-rays diffract in a consistent, predictable way→ structure can be analyzed

Suppose you are studying a newly discovered enzyme. Propose a step-by-step purification strategy and the methods you would use to confirm purity

1. Lyse cells (lysis)

• Process of breaking down or disrupting a cell membrane→ releases intracellular contents

• Can be done chemically (detergents/chemicals), mechanically (physical force such as freezing/thawing), or enzymatically (use enzymes that target and degrade cell membrane)

2. Ultracentrifugation

• spin lysates very fast→ organelles and proteins separate based on density

• Select appropriate on known protein localization or assay fraction

3. Chromatography

• Affinity→ separates based on specific binding, choose matrix based on specific ligand bound by the enzyme

• IEC→ separates based on charge, choose matrix based on net charge of enzyme

• SEC→ removes large aggregates, choose matrix based on size

• A→IEC→SEC is most practical because A is the most specific to the enzyme (decrease in specificity through methods)

4. Purity check

• Utilize an assay to determine presence/purity

The conversion of glycerol + phosphate → glycerol-3-phosphate has a ΔG°’ of +9.2 kJ/mol. Explain why this reaction proceeds in cells, and describe specifically how energy coupling allows this to happen.

This reaction uses energy coupling, involving the hydrolysis of adenosine triphosphate (ATP). The ΔG°’ of the hydrolysis of ATP is -30.5 kJ/mol, so when it is coupled with the conversion of glycerol + phosphate → glycerol-3-phosphate, the conversion becomes thermodynamically favorable through the increase in free energy provided by the hydrolysis of ATP→ total ΔG°’=(-30.5)+9.2= -21.3 kJ/mol

Peptide bond hydrolysis has a ΔG°’ of about –10 kJ/mol, but the half-life of an uncatalyzed peptide bond is roughly 31 years. Explain why a reaction that is thermodynamically favorable can still be kinetically slow, and how an enzyme solves this problem.

Thermodynamics determines spontaneity (ΔG), while kinetics depends on activation energy (ΔG‡). Peptide bond hydrolysis is favorable (–ΔG) but has a huge activation barrier, so it is slow. Enzymes stabilize the transition state, lowering ΔG‡ and increasing the rate

Compare and contrast the lock-and-key and induced fit models of enzyme specificity. Provide an example of how induced fit can increase catalytic efficiency

Lock and key model→ enzymes assume a certain conformation prior to substrate binding that fits the substrate perfectly like a lock and key. (Less accurate)

Induced fit model→ enzymes slightly adjust their conformation upon substrate binding to effectively bind the substrate.

Induced fit can increase catalytic efficiency because it allows the enzyme to change conformation slightly to more tightly bind the transition state→ lowers activation energy and speeds up reaction.

Given the following data for an enzyme-catalyzed reaction ([E]T = 10⁻³ μM): Vmax = 6 μM min⁻¹ KM = 0.5 mM

(a) Calculate kcat.

(b) Calculate kcat/KM and interpret whether this enzyme is near the diffusion-

controlled limit

Vmax= 6 μM min⁻¹→ 6×10^-6 M min^-1→ (divide by 60) 10^-7 M sec^-1

Km= 0.5 mM→ 5×10^-4 M

[E]t= 10^-3μM→ 10^-9 M

kcat= Vmax/[E]t= 10^-7M sec^-1/ 10^-9 M= 100 sec^-1

kcat/Km= 100 sec^-1/ 5×10^-4M= 2×10⁵ M^-1 sec^-1

Not near diffusion controlled limit (approx 10⁹ M^-1 sec^-1) but efficient

You are given a double-reciprocal plot with y-intercept = 0.167 min/μM and x-intercept = –2.0 mM⁻¹.

(a) Determine Vmax and KM.

(b) How would a competitive inhibitor affect the slope and x-intercept of this plot?

1/Vmax= 0.167 min/μM→ Vmax= 5.98 μM/min→(multiply by 10^-6 and divide by 60) 10^-7 M/sec

-1/Km= 2 mM→ Km= 0.5 mM→ (multiply by 10^-3) 5×10^-4 M

A competitive inhibitor would result in a larger/less negative x-intercept (larger Km) and a steeper slope. (slope is Km/Vmax, so a larger Km means a steeper slope) Vmax is NOT affected

Two enzymes catalyze the same reaction:

Enzyme A: kcat = 500 s⁻¹, KM = 10 μM

Enzyme B: kcat = 100 s⁻¹, KM = 1 μM

Which enzyme is more catalytically efficient? Show your calculation and explain why kcat alone is not sufficient to make this judgment

Specificity constant A: 500 s⁻¹/ 10 μM= 50 μM^-1 s⁻¹

Specificity constant B: 100 s⁻¹/ 1μM= 100 μM^-1 s⁻¹

Specificity constant→ expresses catalytic efficiency of an enzyme at converting substrate to product and is expressed as a ratio of kcat/Km. kcat alone is not sufficient to make this judgement because it simply expresses how quickly an enzyme produces a single molecule of P per unit of time and does not account for the difference in affinity of the enzyme for the substrate→ For example, an enzyme with a very high kcat but a low Km may be less efficient in catalysis despite having a high turnover number

A reaction in glycolysis has a ΔG°’ > 0 but still proceeds forward in the cell. Explain how intracellular metabolite concentrations drive the reaction toward product formation despite its positive standard free energy change.

Because the overall reaction favorability depends both on the value of ΔG°’ and the value of RT*ln([P]/[R])→ overall free energy is determined by the equation ΔG= ΔG°’+ RT*ln([P]/[R]), so if the ratio of [P]:[R] is low (low product conc and high substrate conc) through metabolite control (ex. energy coupling/rapid product removal), ΔG can become negative and the reaction can proceed.

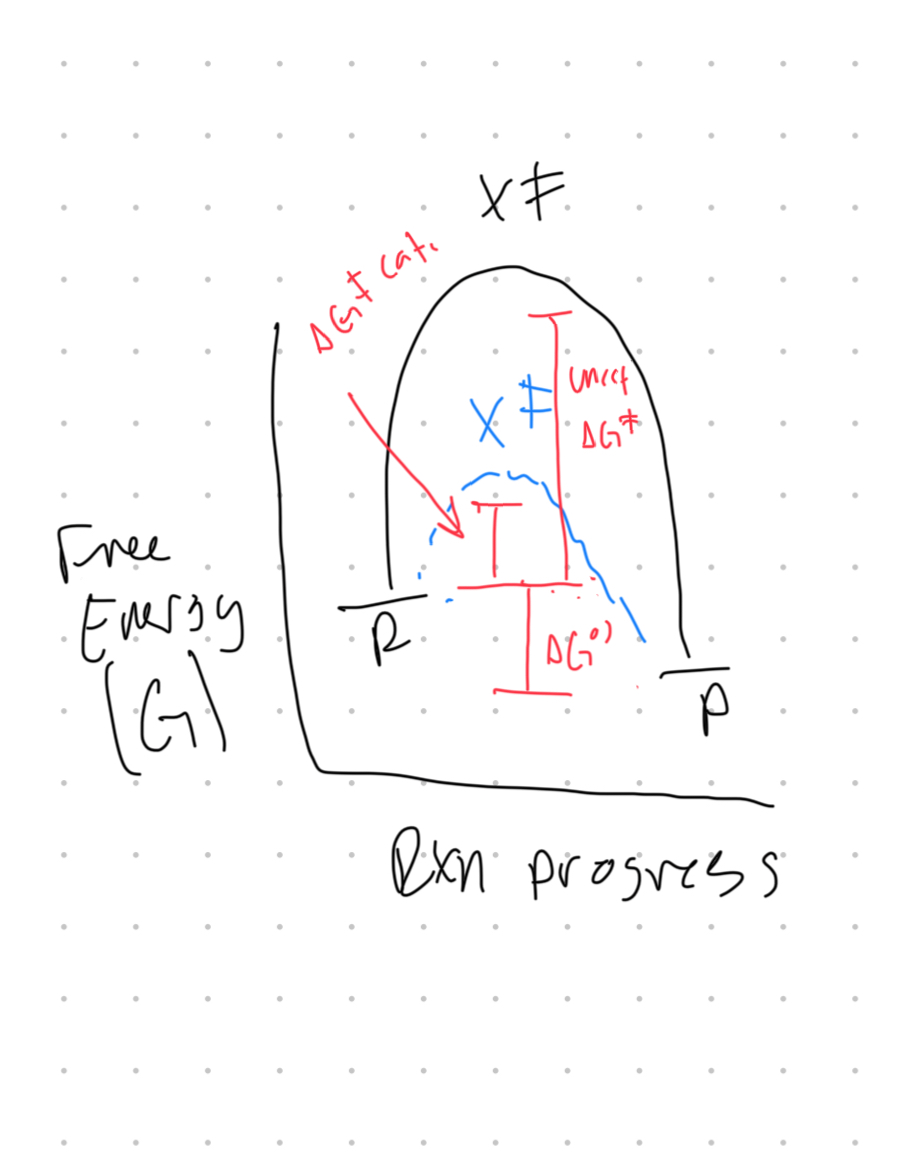
Draw an energy diagram showing how an enzyme lowers the activation energy (ΔG‡) without changing ΔG°’. Explain why this does not affect the equilibrium constant.

Enzymes catalyze reactions by lowering the activation energy (ΔG‡)/stabilizing the transition state. They do not impact the free energy of the reactants or products, so ΔG°’ (dif. in free energy of products and reactants) remains unchanged. The equilibrium constant remains the same because enzymes impact the speed at which equilibrium is reached not the equilibrium itself.

Imagine an enzyme that follows Michaelis-Menten kinetics but exhibits a sigmoidal rate curve when a regulatory molecule binds. Explain what type of regulation this represents and how it might affect Vmax and/or KM.

This indicates cooperativity induced by the binding of an allosteric effector at a regulatory site. Allosteric effectors bind at regulatory sites and typically cause conformational changes that impact ligand binding at functional sites→cooperativity→sigmoidal binding curve.

This would likely lower Vmax and increase Km, because M-M kinetics are hyperbolic, indicating a conformation that readily allows binding. Allosteric effectors can cause a conformational change to a lower affinity state that exists in equilibrium with the higher affinity conformation. Because of this equilibrium, there will be a decrease in both max. reaction velocity when saturated with substrate and overall affinity.