COMP306 #12 Hash Based Indexing

the motivation for indexing in general

if your table is very large linear search will be very slow (full table scan).

what is an index in the context of dbms

a data structure that enables locating data quickly without having to do a full table scan.

what is hash-based indexing good for?

equality selections (condition in the where clause is like something = something), not so good for range selection

which index do we use for range selections

tree based indexes.

CREATE INDEX

where are indexes also used?

in the internals of the dbms.

disadvantages of indexes.

must be updated when the table are,

also before they are updated, they should be locked, potentially affecting other transaction’s throughput.

indexes cost space.

general advice for indexes

create them when they are useful but don’t create redundant indexes!

a hash table

an associative array that maps keys to values

a hash function

used to map data of arbitrary size into fixed size values e.g. integers

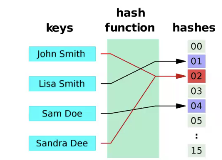
hash collision

when two different keys are mapped to the same hash value.

desired properties of hash functions

quick to compute (not necessarily cryptographically secure), low collision rate.

static hashing

allocate a large array that has one slot for each record.

each slot holds one record.

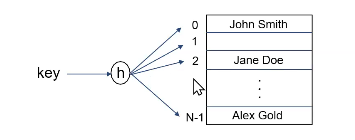
potential hash fn for static hashing

h(k) mod N, where N: #of records.

static hashing works fine when

you know the #of records (N) ahead of time
hash function is perfect, i.e. no hash collisions.

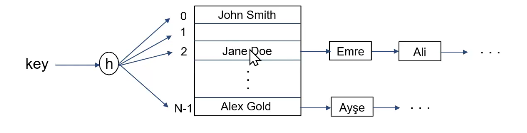
Overflow chaining

a straightforward extension of static hashing to handle hash collisions, if there is a hash collision create overflow buckets

overflow buckets become a chain (can be treated like a linked list)

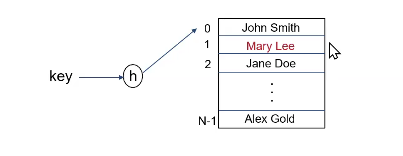
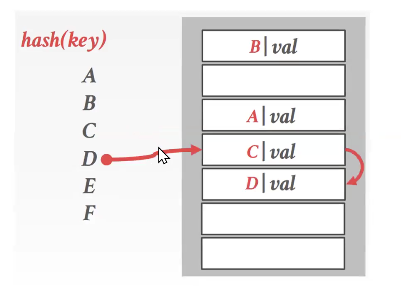
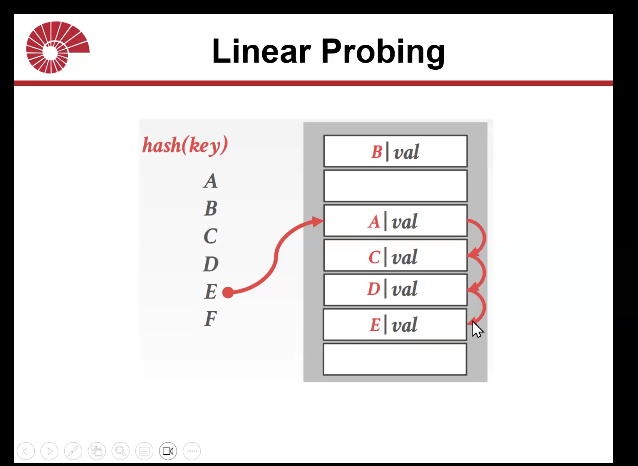
linear probing

another extension of static hashing to handle hash collisions

resolve collisions by linear seraching (probing) for the next free slot in the hash table

hash to the key’s location and start scanning.

when you find an empty slot, insert the record there.

the problem with linear probing delete

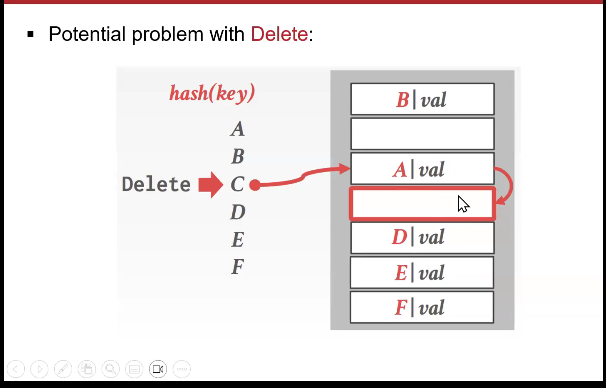
we delete c and try to find d.

well, if this empty, maybe d isn’t in the table? that would be incorrect, so we have to mark the cells as deleted.

linear probing deletion solution

the tombstone approach

if we approach a tombstone well carry on searching bozo 😂

non-unique hash keys

for simplicity, we’ll make the assumption that our hash keys are unique.

handling non-unique keys

store duplicate key’s entries separately in the hashtable
same ide can be used in other hashing schemes as well

in which way is extendible hashing different than static hashing?

it is a dynamic hashing approach

extendible hashing

directory contains pointers to buckets

to find the bucket for r, take the last global depth #of bits of h®

h® = 5 = binary 101 so it is placed in bucket pointed by 01

we represent r by h® in the figures for clarity.

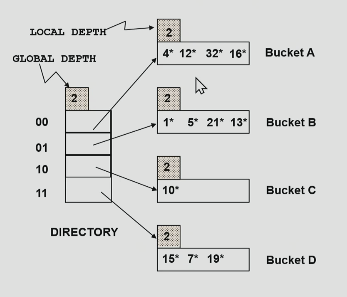
extendible hashing

lecture explains it quite well, it has a lot to do with least significant bits.

global depth in extendible hashing

the number of least significant bits which consider the hash value.

local depth in extendible hashing

it determines how many least significant bits that bucket looks at.

when a bucket is full and a new insertion arrives the bucket should

split, the directory may or may not have to double when a split occurs.

compare global depth vs local dept.

splitting (causing directory doubling)

when local depth > global depth

notice that buckets B, C, D are not modified by insertion of 20.

extendible hashing deletions

if bucket becomes empty and has a split image, they merge.

if each directory element points to same bucket as its split image, halve the directory.

linear hashing

as opposed to extendible hashing, always split the bucket that is pointed by the “next” pointer

splitting is not guaranteed to fix overflows

next pointer is linear - will eventually get to overflows

if no overflow, no need to split or advance Next pointer.

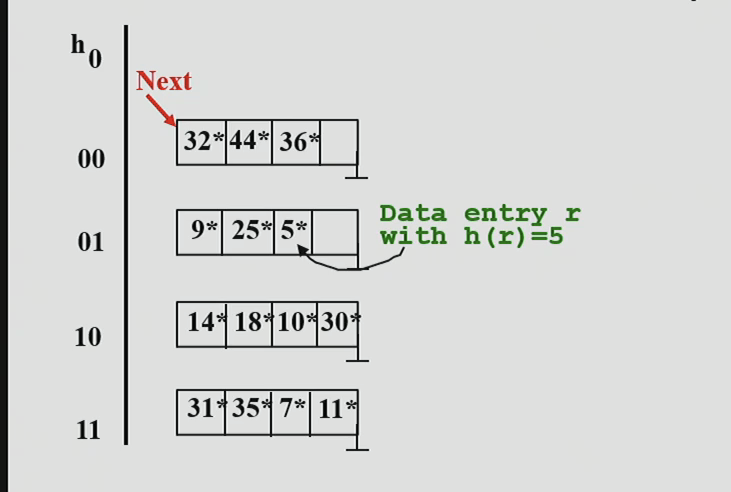
h0 represents our initial hash level.

linear hashing similartity with extendible hashing

the binary idea remains the same.

what causes splitting at the next pointer and it being moved?

inserting into an overflow (so it can be the first overflow i.e. inserting into a full bucket for the first time, or it can be another insertion while overflow).

how can the next pointer move to the beginning instead of moving on to the next bucket?

if it has does one pass over the hash level. it will move to the next hash level.

deletion in a linear hash

issue here.

delete 7 and 31.

strategy #1: merge buckets, decrement next pointer
when there’s a new overflow eventually, you’ll need to re-do the work and the splitting
you may again end up with an empty bucket.

strategy #2: do nothing (let the bucket remain empty)
cannot reclaim previously allocated memory
this is the strategy will use