Nummód I.
5.0(8)
Card Sorting
1/211
Earn XP
Description and Tags
Beugró kérdések a nummód I. (B) vizsgához. Véletlen került bele néhány nummód II.es is.¯\_(ツ)_/¯
Last updated 1:50 PM on 6/19/23
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
212 Terms
1
New cards
Melyik állítás igaz az alábbiak közül az A = UDV\* szinguláris felbontásra?
(A) A U oszlopai az A\*A mátrix sajátvektorai
(B) A V oszlopai az AA\* mátrix sajátvektorai
(C) D nem nulla elemei az A szinguláris értékei.
(A) A U oszlopai az A\*A mátrix sajátvektorai
(B) A V oszlopai az AA\* mátrix sajátvektorai
(C) D nem nulla elemei az A szinguláris értékei.
C) D nem nulla elemei az A szinguláris értékei.
2
New cards
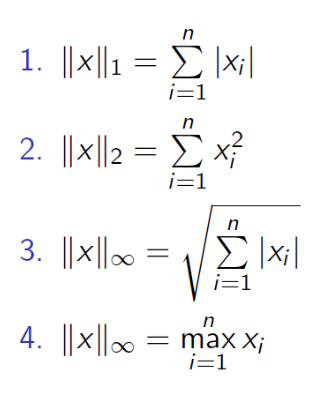
Legyen n ∈ N+ és x ∈ Rⁿ vektor. Az alábbi összefüggések közül melyik helyes?
\
\
3
New cards
Az alábbiak közül melyik formula alkalmazható az A mátrix 2-es kondíciószámának kiszámításához, ha b ≠ 0?
\
(A) cond₂ (A) = ||A||₂ \* ||A⁻¹||₂
(B) cond₂ (A) = max |λᵢ (A)| / min |λᵢ (A)|
(C) Mindkettő
(D) Egyik sem
\
(A) cond₂ (A) = ||A||₂ \* ||A⁻¹||₂
(B) cond₂ (A) = max |λᵢ (A)| / min |λᵢ (A)|
(C) Mindkettő
(D) Egyik sem
(A) cond₂ (A) = ||A||₂ \* ||A⁻¹||₂
4
New cards
Ha az A mátrix sajátértékei: -3, -1, 0, 1, 3, akkor az A - pl eltolásra alkalmazott hatványmódszer mikor a leggyorsabb az alábbiak közül?
(A) p = -3 esetén.
(B) p = -1 esetén.
(C) p = -2 esetén.
(A) p = -3 esetén.
(B) p = -1 esetén.
(C) p = -2 esetén.
(B) p = -1 esetén.
5
New cards
Melyik állítás igaz a hasonló mátrixokra?
(A) A hasonló mátrixok nyoma azonos.
(B) Ha a mátrixok hasonlók, akkor invertálhatóak.
(C) A szimmetrikus mátrixhoz hasonló mátrixok is szimmetrikusak.
(A) A hasonló mátrixok nyoma azonos.
(B) Ha a mátrixok hasonlók, akkor invertálhatóak.
(C) A szimmetrikus mátrixhoz hasonló mátrixok is szimmetrikusak.
(A) A hasonló mátrixok nyoma azonos.
6
New cards

C
7
New cards
A Jacobi-módszer esetén a diagonálison kívüli elemek négyzetösszege milyen ütemben tart nullához?
(A) 1/n(n-1)-gyel arányosan csökken.
(B) Mértani nullasorozattal majorálhatóan.
(C) 2/n(n-1)-gyel arányosan csökken.
(A) 1/n(n-1)-gyel arányosan csökken.
(B) Mértani nullasorozattal majorálhatóan.
(C) 2/n(n-1)-gyel arányosan csökken.
(B) Mértani nullasorozattal majorálhatóan.
8
New cards

C
9
New cards
Szimmetrikus (önadjungált) mátrix esetén melyik állítás nem igaz a reziduum vektorra?
(A) Becsülhető vele a sajátvektor.
(B) A Rayleigh-hányados minimalizálja a 2-es normáját.
(C) Becsülhető vele a sajátérték közelítés jósága.
(A) Becsülhető vele a sajátvektor.
(B) A Rayleigh-hányados minimalizálja a 2-es normáját.
(C) Becsülhető vele a sajátérték közelítés jósága.
A) Becsülhető vele a sajátvektor.
10
New cards

A
11
New cards
Válassza ki a helyes állítást
(A) A ∥ · ∥2-es mátrixnorma illeszkedik a ∥ · ∥2-es vektornormára.
(B) A ∥ · ∥F mátrixnorma illeszkedik a ∥ · ∥2-es vektornormára.
(C) (A) és (B) is hamis.
(D) (A) és (B) is igaz
(A) A ∥ · ∥2-es mátrixnorma illeszkedik a ∥ · ∥2-es vektornormára.
(B) A ∥ · ∥F mátrixnorma illeszkedik a ∥ · ∥2-es vektornormára.
(C) (A) és (B) is hamis.
(D) (A) és (B) is igaz
(D) (A) és (B) is igaz
12
New cards
Túlhatározott teljes rangú esetben az általánosított inverz számítására melyik képlet használható?
\
(A) A+ = A\*(AAᵀ)⁻¹
(B) A+ = (A\*A)⁻¹A\*
(C) A+ = A(A\*A)⁻¹
(D) A+ = (A\*A)⁻¹A
\
(A) A+ = A\*(AAᵀ)⁻¹
(B) A+ = (A\*A)⁻¹A\*
(C) A+ = A(A\*A)⁻¹
(D) A+ = (A\*A)⁻¹A
(B)
13
New cards

(C)
14
New cards
Legyen a = 2 egy ∆a = 1 hibával terhelt mennyiség. Az alábbi lehetőségek közül mi lehet ∆f (a) értéke, ha f (x) = x^2 + 1.
(A) ∆f (a) = 6.
(B) ∆f (a) = 5.
(C) ∆f (a) = 4.
(D) ∆f (a) = 3.
(A) ∆f (a) = 6.
(B) ∆f (a) = 5.
(C) ∆f (a) = 4.
(D) ∆f (a) = 3.
(A) ∆f (a) = 6.
15
New cards
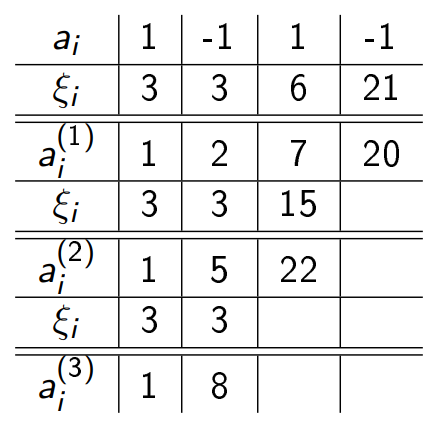
Az alábbi, P értékeire vonatkozó Horner-algoritmusból adódó táblázat alapján mi lesz P ′′(3)?
(A) 16
(B) 8
(C) 24
(D) 20
(A) 16
(B) 8
(C) 24
(D) 20
(A) 16
16
New cards

(B)
17
New cards

(B)
18
New cards

(C)
19
New cards
Tegyük fel, hogy az M(t, k −, 1) gépi számhalmaz esetén ε1 < ε0. Az alábbi állítások közül melyik igaz a számábrázolás pontosságát illetően bármely ábrázolható x ∈ R esetén?
(A) |x − fl(x)| ≤ ε0|x|/2
(B) |x − fl(x)| ≤ ε0
(C) |x − fl(x)| ≤ ε1|x|/2
(D) |x − fl(x)| ≤ ε1/2
(A) |x − fl(x)| ≤ ε0|x|/2
(B) |x − fl(x)| ≤ ε0
(C) |x − fl(x)| ≤ ε1|x|/2
(D) |x − fl(x)| ≤ ε1/2
(B) |x − fl(x)| ≤ ε0
20
New cards

(C)
21
New cards
Az alábbiak közül melyik lineáris spline a \[0,4\] intervallumon?
(A) x+1 (0≤ x
(A) x+1 (0≤ x
(D) 2-x (0≤ x
22
New cards
Legyen H Hilbert-tér (R felett) és gᵢ ∈ H (i = 1... ..n) lineárisan függetlenek. Ekkor a Gram-mátrix nem feltétlenül
(A) szimmetrikus.
(B) diagonális.
(C) pozitív definit.
(D) invertálható.
(A) szimmetrikus.
(B) diagonális.
(C) pozitív definit.
(D) invertálható.
(B) diagonális.
23
New cards

D
24
New cards
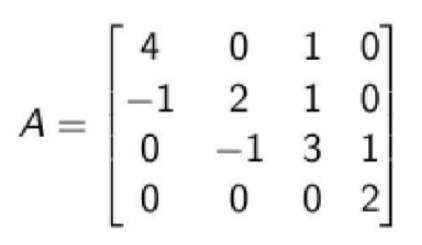
Szigorúan diagonálisan domináns-e az alábbi mátrix?
* Igen, a soraira.
* Igen, az oszlopaira.
* Igen, a soraira és az oszlopaira is.
* Se a soraira, se az oszlopaira.
* Igen, a soraira.
* Igen, az oszlopaira.
* Igen, a soraira és az oszlopaira is.
* Se a soraira, se az oszlopaira.
Canvas szerint: Igen, a soraira és az oszlopaira is. Definíció alapján: Igen, az oszlopaira.
25
New cards
Tekintsük az alábbi interpolációs alappontokat: x₀ = 0, x1 = 1, x₂ = 2. Melyik nem lesz az adott alappontokhoz tartozó Lagrange-alappolinom?
\
* (x-1)(x-2)/2
* x(x-2)/2
* x(x-1)/2
\
* (x-1)(x-2)/2
* x(x-2)/2
* x(x-1)/2
x(x-2)/2
26
New cards
Tekintsük az M(t, k- ,k+) gépi számok halmazat! M∞, ε0, ε1 ábrázolás nevezetes paraméterei. Melyik formula helyes az alábbiak közül:
\
* M∞ = 2ᵏ⁺
* ε0 = 2ᵏ⁻
* ε1 = 2¹⁻ᵗ
\
* M∞ = 2ᵏ⁺
* ε0 = 2ᵏ⁻
* ε1 = 2¹⁻ᵗ
ε1 = 2¹⁻ᵗ
27
New cards
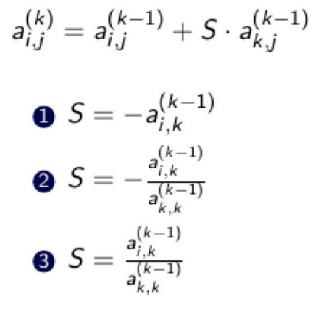
Mi az S helyes értéke a Gauss-elimináció transzformációs képletében?
\
\
2
28
New cards
Legyen ||x|| egy rögzített vektornorma, ||Al| pedig az általa indukált mátrixnorma. Legyen továbbá ||A||ₘ, egy tetszőleges mátrix norma. Ha teljesül az alábbi egyenlőtlenség ||Ax|| < ||A||ₘ ||x|| minden x vektorra, melyik igaz az alábbi összefüggések közül?
\
* ||A|| = ||A||ₘ
* ||A|| ≤ ||A||ₘ
* ||A|| > ||A||ₘ
\
* ||A|| = ||A||ₘ
* ||A|| ≤ ||A||ₘ
* ||A|| > ||A||ₘ
||A|| ≤ ||A||ₘ
29
New cards

Melyik nem igaz a mátrix kondíció számával kapcsolatos összefüggések közül? Legyen A invertálható mátrix, cond(A) jelölje a kondíció számát!
2
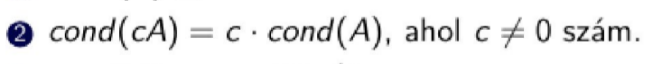
30
New cards
A φ(x) függvény melyik fontos tulajdonsága következik az alábbi feltételből? φ ∈ C1\[a, b\] és
|φ’(x)| < 1 teljesül ∀ x ∈ \[a, b\]?
* A φ szigorúan monoton növekedő függvény \[a, b\] intervallumon.
* ∃ x\* ∈ \[a, b\] úgy, hogy x\* *=* φ(x\*)
* A φ függvény kontrakció az \[a, b\] intervallumon.
* A φ függvénynek van zérushelye az \[a, b\] intervallumon.
|φ’(x)| < 1 teljesül ∀ x ∈ \[a, b\]?
* A φ szigorúan monoton növekedő függvény \[a, b\] intervallumon.
* ∃ x\* ∈ \[a, b\] úgy, hogy x\* *=* φ(x\*)
* A φ függvény kontrakció az \[a, b\] intervallumon.
* A φ függvénynek van zérushelye az \[a, b\] intervallumon.
A φ függvény kontrakció az \[a, b\] intervallumon.
31
New cards
Ha P tetszőleges polinom és valamely ξ helyen P(x) = P(ξ) + (x - ξ)Q(x), akkor az alábbiak közül mi teljesül a Q polinomra?
\
(A) ∃x ∈ R: P’(x) = Q(x)
(B) ∀x ∈ R: P’(x) ≠ Q(x)
(C) ∀x ∈ R: P’(x) = Q(x)
(D) ∀x ∈ R: P(x) = Q’(x)
\
(A) ∃x ∈ R: P’(x) = Q(x)
(B) ∀x ∈ R: P’(x) ≠ Q(x)
(C) ∀x ∈ R: P’(x) = Q(x)
(D) ∀x ∈ R: P(x) = Q’(x)
(A) ∃x ∈ R: P’(x) = Q(x)
32
New cards
Tegyük fel, hogy az M(t, k, k) gépi számhalmazban M∞ = 63. Mi következik ebből?
* k = 2
* k = 4
* k = 6
* k = 8
* k = 2
* k = 4
* k = 6
* k = 8
k = 6
33
New cards
Legyen n ∈ N, n ≥ 3. A polinomok gyökeinek becslésére tanult tétel alapján mennyi a (R - 1)/r mennyiség értéke a
xⁿ/n + xⁿ⁻¹/n-1 + …… + x²/2 + x + 2
polinom esetén?
* 2
* n/3
* 3/n
* 3n
xⁿ/n + xⁿ⁻¹/n-1 + …… + x²/2 + x + 2
polinom esetén?
* 2
* n/3
* 3/n
* 3n
3n
34
New cards
Tegyük fel, hogy a φ függvényre teljesülnek a Brouwer-féle fixponttétel feltételei. Melyik állítás hamis az alábbiak közül?
* ∃ x\* ∈ \[a, b\] úgy, hogy φ(x\*) = x\*
* φ : \[a, b\] → \[a, b\]
* φ kontrakció
* φ ∈ C\[a, b\]
* ∃ x\* ∈ \[a, b\] úgy, hogy φ(x\*) = x\*
* φ : \[a, b\] → \[a, b\]
* φ kontrakció
* φ ∈ C\[a, b\]
φ kontrakció
35
New cards

Legyen A ∈ Rⁿˣⁿ egy szimmetrikus pozitív definit mátrix, A⁽¹⁾ pedig a Gauss-elimináció első lépésében kapott felsőháromszög mátrix. Milyen állítások igazak A⁽¹⁾ jobb alsó (bekeretezett) B ∈ R⁽ⁿ⁻¹⁾ˣ⁽ⁿ⁻¹⁾ sarok mátrixára?
\
* B szimmetrikus
* det(B) ≠ 0
* B szimmetrikus és pozitív definit.
* Mindegyik
\
* B szimmetrikus
* det(B) ≠ 0
* B szimmetrikus és pozitív definit.
* Mindegyik
* Mindegyik
36
New cards

Az alábbi iterációk közül melyik lesz bizonyos feltételek mellett másodrendben konvergens iteráció?
1
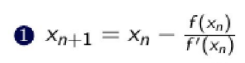
37
New cards
Az alábbi feltételek adottak a Newton iteráció monoton konvergencia tételének feltételei közül:
* f ∈ C2\[a, b\]
* ∃ x\* ∈ \[a, b\] úgy, hogy f(x\*) = 0
* f’(x) ≠ 0 és f’’(x) ≠0
Melyik a hiányzó feltétel az alábbiak közül?
* x₀ ∈ \[a, b\] tetszőleges.
* x₀ ∈ \[a, b\] úgy, hogy f(x₀)f’’(x₀) < 0
* x₀ ∈ \[a, b\] úgy, hogy f(x₀)f’’(x₀) > 0
* x₀ ∈ \[a, b\] úgy, hogy f(x₀)f’’(x₀) = 0
* f ∈ C2\[a, b\]
* ∃ x\* ∈ \[a, b\] úgy, hogy f(x\*) = 0
* f’(x) ≠ 0 és f’’(x) ≠0
Melyik a hiányzó feltétel az alábbiak közül?
* x₀ ∈ \[a, b\] tetszőleges.
* x₀ ∈ \[a, b\] úgy, hogy f(x₀)f’’(x₀) < 0
* x₀ ∈ \[a, b\] úgy, hogy f(x₀)f’’(x₀) > 0
* x₀ ∈ \[a, b\] úgy, hogy f(x₀)f’’(x₀) = 0
x₀ ∈ \[a, b\] úgy, hogy f(x₀)f’’(x₀) > 0
38
New cards

Az interpoláció hibatételének feltételei mellett, a bizonyításban szereplé gₓ(z) függvényre melyik nem igaz?
\
\
2
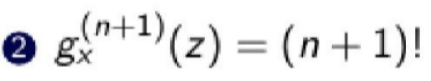
39
New cards
Az alábbi számok közül melyiket nem tartalmazza az M(6,-1,5) számhalmaz?
(A) - \[01101| 0\]
(B) - \[01101| -1\]
(C) - \[10101| 2\]
(D) - Egyiket sem
(A) - \[01101| 0\]
(B) - \[01101| -1\]
(C) - \[10101| 2\]
(D) - Egyiket sem
(D) - Egyiket sem
40
New cards
Ha az e szám értékét 3-mal közelítjük, melyik a jó abszolút hibakorlát az alábbiak közül?
(A) - △₃ = 0.15
(B) - △₃ = 0.3
(C) - △₃ = 0.05
(D) - Egyik sem
(A) - △₃ = 0.15
(B) - △₃ = 0.3
(C) - △₃ = 0.05
(D) - Egyik sem
(B) - △₃ = 0.3
41
New cards
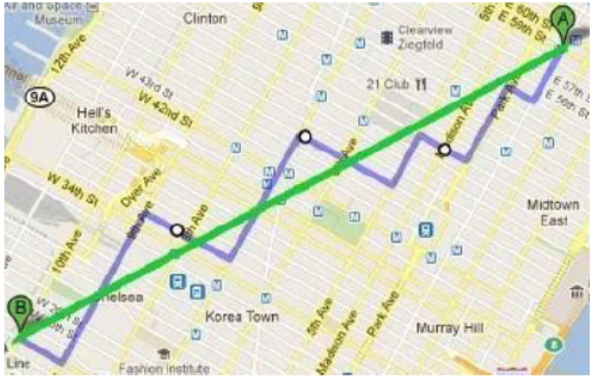
Egy városban csak észak-déli, kelet-nyugati irányú utcákon közlekedhetünk. A fenti ábrán a kék vonal egy olyan megengedett útvonalat szemléltet, melyen el lehet jutni A-ból B-be. A zöld vonal nem egy valós útvonal, mert átlós utak nincsenek. Ha az A és B pontokat kétdimenziós vektorokkal adjuk meg, akkor a kékkel jelölt útvonal hossza melyik távolságnak felel meg?
(A) - ||A-B||₂
(B) - ||A-B||₁
(C) - ||A-B||∞
(D) - ||A-B||F
(A) - ||A-B||₂
(B) - ||A-B||₁
(C) - ||A-B||∞
(D) - ||A-B||F
(B) - ||A-B||₁
42
New cards
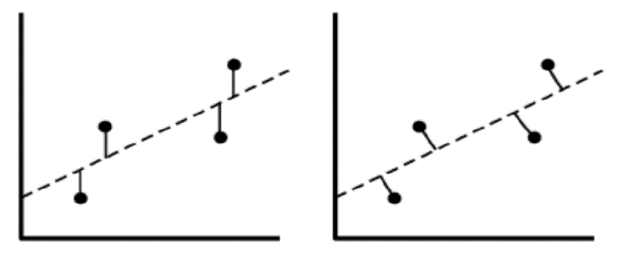
Melyik ábra szerinti távolságok négyzetösszegét minimalizálja az előadáson tanult legkisebb négyezetes egyenesillesztés?
(A) A bal oldali ábrán lévő távolságokat.
(B) A jobb oldali ábrán lévő távolságokat.
(C) Mindkettőt.
(D) Egyiket sem.
(A) A bal oldali ábrán lévő távolságokat.
(B) A jobb oldali ábrán lévő távolságokat.
(C) Mindkettőt.
(D) Egyiket sem.
(A) A bal oldali ábrán lévő távolságokat.
43
New cards
Tekintsük az (xᵢ, yᵢ), i = 0,….,n alappontokra illeszkedő interpolációs polinom Lagrange-alakját Lₙ(x) és a Newton-alakját Nₙ(x). Melyik állítás igaz az alábbiak közül?
(A) ∃ x ∈ R: Lₙ(x) ≠ Nₙ(x)
(B) ∀ x ∈ R: Lₙ(x) = Nₙ(x)
(C) ∀ x ∈ R: Lₙ(x) = Nₙ(x) + Nₙ₋₁(x)
(D) Mindegyik igaz.
(A) ∃ x ∈ R: Lₙ(x) ≠ Nₙ(x)
(B) ∀ x ∈ R: Lₙ(x) = Nₙ(x)
(C) ∀ x ∈ R: Lₙ(x) = Nₙ(x) + Nₙ₋₁(x)
(D) Mindegyik igaz.
(B) ∀ x ∈ R: Lₙ(x) = Nₙ(x)
44
New cards
Legyen x ∈ Rⁿ . Ekkor:
(A) ||x||p ≤ ||x||q, ha p ≥ q ≥ 1
(B) ||x||p ≤ ||x||q, ha p ≤ q ≥ 1
(C) ||x||p ≥ ||x||q, ha p ≤ q ≥ 1
(D) ||x||p ≥ ||x||q, ha p ≥ q ≥ 1
(A) ||x||p ≤ ||x||q, ha p ≥ q ≥ 1
(B) ||x||p ≤ ||x||q, ha p ≤ q ≥ 1
(C) ||x||p ≥ ||x||q, ha p ≤ q ≥ 1
(D) ||x||p ≥ ||x||q, ha p ≥ q ≥ 1
(A) ||x||p ≤ ||x||q, ha p ≥ q ≥ 1
45
New cards
Legyenek az A ∈ Rⁿˣⁿ szimmetrikus mátrix sajátértékei: λ₁,λ₂,….,λₙ. Ha tudjuk, hogy minden i = 1,…,n esetén λᵢ > 0, akkor mit lehet mondani A egy tetszőleges Schur-komplementerének \[A|A₁₁\] sajátértékeiről?
(A) \[A|A₁₁\] -nak csak negatív sajátértékei vannak.
(B) \[A|A₁₁\] -nak csak pozitív sajátértékei vannak.
(C) \[A|A₁₁\] -nak pozitív és negatív sajátértékei vannak.
(D) \[A|A₁₁\] -nak lesz nulla sajátértéke.
(A) \[A|A₁₁\] -nak csak negatív sajátértékei vannak.
(B) \[A|A₁₁\] -nak csak pozitív sajátértékei vannak.
(C) \[A|A₁₁\] -nak pozitív és negatív sajátértékei vannak.
(D) \[A|A₁₁\] -nak lesz nulla sajátértéke.
(B) \[A|A₁₁\] -nak csak pozitív sajátértékei vannak.
46
New cards

2
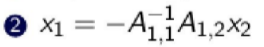
47
New cards
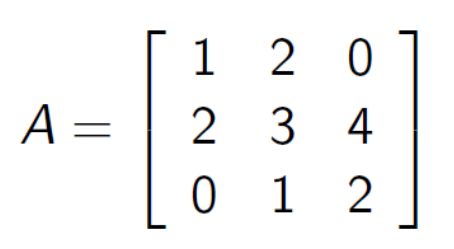
Az alábbi mátrixxal felírt Ax = b lineáris egyenletrendszert melyik tanult módszerrel oldhatjuk meg a legkevesebb művelettel?
(A) Gauss-eliminációval.
(B) LU felbontással.
(C) Progonka módszerrel.
(D) Mindegyik ugyanannyi műveletet igényel.
(A) Gauss-eliminációval.
(B) LU felbontással.
(C) Progonka módszerrel.
(D) Mindegyik ugyanannyi műveletet igényel.
(C) Progonka módszerrel.
48
New cards
Az M := M(t, k-, k+) gépi számhalmazra vonatkozó állítások közül melyik igaz?
(A) M tartalmazza a 0-t.
(B) Bármely 2 szomszédos elem távolsága azonos.
(C) M elemei ε₀-ra szimmetrikusan helyezkednek el.
(D) M páros számú elemet tartalmaz.
(A) M tartalmazza a 0-t.
(B) Bármely 2 szomszédos elem távolsága azonos.
(C) M elemei ε₀-ra szimmetrikusan helyezkednek el.
(D) M páros számú elemet tartalmaz.
(A) M tartalmazza a 0-t.
49
New cards
Az alapműveletek hibakorlátaira vonatkozó ismereteink szerint mely állítás hamis?
\
(A) Két egymáshoz közeli szám összegének képzése nem növeli nagy mértékben az eredmény relatív hibakorlátját.
(B) Két egymáshoz közeli szám összegének képzése nem növeli nagy mértékben az eredmény abszolút hibakorlátját.
(C) Két egymáshoz közeli szám különbségének képzése nem növeli nagy mértékben az eredmény relatív hibakorlátját.
(D) Két egymáshoz közeli szám különbségének képzése nem növeli nagy mértékben az eredmény abszolút hibakorlátját.
\
(A) Két egymáshoz közeli szám összegének képzése nem növeli nagy mértékben az eredmény relatív hibakorlátját.
(B) Két egymáshoz közeli szám összegének képzése nem növeli nagy mértékben az eredmény abszolút hibakorlátját.
(C) Két egymáshoz közeli szám különbségének képzése nem növeli nagy mértékben az eredmény relatív hibakorlátját.
(D) Két egymáshoz közeli szám különbségének képzése nem növeli nagy mértékben az eredmény abszolút hibakorlátját.
(C) Két egymáshoz közeli szám különbségének képzése nem növeli nagy mértékben az eredmény relatív hibakorlátját.
50
New cards
Az Ax = b lineáris egyenletrendszer megoldását Gauss-elimináció segítségével szeretnénk kiszámítani. Az alábbi állítások közül melyik igaz?
\
(A) Ha det(A) = 0, akkor a Gauss-elimináció nem hajtható végre sor- és oszlopcsere nélkül.
(B) Ha det(A) = 0, akkor a lineáris egyenletrendszernek biztosan nincs megoldása.
(C) Ha det(A) ≠ 0, akkor a Gauss-elimináció lehet, hogy nem hajtható végre sor- és oszlopcsere nélkül.
(D) Ha det(A) ≠ 0, akkor a lineáris egyenletrendszernek lehet, hogy két megoldása van.
\
(A) Ha det(A) = 0, akkor a Gauss-elimináció nem hajtható végre sor- és oszlopcsere nélkül.
(B) Ha det(A) = 0, akkor a lineáris egyenletrendszernek biztosan nincs megoldása.
(C) Ha det(A) ≠ 0, akkor a Gauss-elimináció lehet, hogy nem hajtható végre sor- és oszlopcsere nélkül.
(D) Ha det(A) ≠ 0, akkor a lineáris egyenletrendszernek lehet, hogy két megoldása van.
(C) Ha det(A) ≠ 0, akkor a Gauss-elimináció lehet, hogy nem hajtható végre sor- és oszlopcsere nélkül.
51
New cards
Az Ax = b lineáris egyenletrendszer megoldását Gauss-elimináció segítségével szeretnénk kiszámítani. Az alábbi állítások közül melyik igaz?
\
(A) Ha det(A) = 0, akkor a Gauss-elimináció nem hajtható végre sor- és oszlopcsere nélkül.
(B) Ha det(A) = 0, akkor a lineáris egyenletrendszernek lehet, hogy nincs megoldása.
(C) Ha det(A) ≠ 0, akkor a Gauss-elimináció végrehajtható sor- és oszlopcsere nélkül.
(D) Ha det(A) ≠ 0, akkor a lineáris egyenletrendszernek lehet, hogy két megoldása van.
\
(A) Ha det(A) = 0, akkor a Gauss-elimináció nem hajtható végre sor- és oszlopcsere nélkül.
(B) Ha det(A) = 0, akkor a lineáris egyenletrendszernek lehet, hogy nincs megoldása.
(C) Ha det(A) ≠ 0, akkor a Gauss-elimináció végrehajtható sor- és oszlopcsere nélkül.
(D) Ha det(A) ≠ 0, akkor a lineáris egyenletrendszernek lehet, hogy két megoldása van.
(B) Ha det(A) = 0, akkor a lineáris egyenletrendszernek lehet, hogy nincs megoldása.
52
New cards
Az f(x) = e⁻ˣ² = 0 megoldását szeretnénk közelíteni az \[1;2\] intervallumon Newton-módszer segítségével. Milyen x₀-ból indítva kapunk konvergens eljárást?
(A) Csak x₀ > x\* esetén.
(B) Csak x₀ < x\* esetén.
(C) A Newton-módszer nem lesz konvergens ebben az esetben.
(D) Bármely x₀ ∈ \[1; 2\] esetén konvergens a Newton-módszer.
(A) Csak x₀ > x\* esetén.
(B) Csak x₀ < x\* esetén.
(C) A Newton-módszer nem lesz konvergens ebben az esetben.
(D) Bármely x₀ ∈ \[1; 2\] esetén konvergens a Newton-módszer.
(C) A Newton-módszer nem lesz konvergens ebben az esetben.
53
New cards
Legyen adott v ∈ Rⁿ olyan, hogy ||v||₂ =1, és x ∈ Rⁿ. Tegyük fel, hogy H(v)(H(v)x) = x, ahol H(v) a v-hez tartozó Householder-mátrix.
Ekkor:
(A) v ⊥ x,
(B) v=x,
(C) (A) és (B) is lehetséges.
Ekkor:
(A) v ⊥ x,
(B) v=x,
(C) (A) és (B) is lehetséges.
(C) (A) és (B) is lehetséges.
54
New cards
Melyik mátrixnorma nem indukált az alábbiak közül?
\
(A) ||.||₁
(B) ||.||₂
(C) Minden mátrixnorma indukált.
(D) ||.||F
\
(A) ||.||₁
(B) ||.||₂
(C) Minden mátrixnorma indukált.
(D) ||.||F
(D) ||.||F
55
New cards
Tekintsünk egy 23 pontra épülő interpolációs feladatot! Hány darab harmadrendű osztott differencia tartozik az adott osztópont rendszerhez?
\
(A) 20
(B) 21
(C) 19
(D) 0
\
(A) 20
(B) 21
(C) 19
(D) 0
(A) 20
56
New cards
Mely feltétel nem szükséges a Newton módszer lokális konvergenciájához?
\
(A) f ∈ C²\[a,b\]
(B) ∃m > 0 : ∀x ∈ (a,b): |f’(x)| < m
(C) ∃M> 0 : ∀x ∈ (a,b): |f’’(x)| < M
(D) Mindháromra szükség van.
\
(A) f ∈ C²\[a,b\]
(B) ∃m > 0 : ∀x ∈ (a,b): |f’(x)| < m
(C) ∃M> 0 : ∀x ∈ (a,b): |f’’(x)| < M
(D) Mindháromra szükség van.
(B) ∃m > 0 : ∀x ∈ (a,b): |f’(x)| < m
57
New cards
Az alábbiak közül melyik intervallumon van fixpontja az f(x) := x³ - 3x függvénynek?
\
(A) \[2.5;3\].
(B) \[-1;-0.5\].
(C) \[4;5\].
(D) \[0;2\].
\
(A) \[2.5;3\].
(B) \[-1;-0.5\].
(C) \[4;5\].
(D) \[0;2\].
(D) \[0;2\].
58
New cards
Melyik állítás igaz az n-fokú polinomokra tanult Horner algoritmusra?
\
(A) Műveletigénye a fokszámmal négyzetes arányban nő.
(B) Tetszőleges folytonos függvény gyökeinek meghatározására alkalmazható.
(C) Szélsőérték meghatározására is közvetlenül alkalmazható.
(D) Polinom deriváltjainak kiszámítására is alkalmazható.
\
(A) Műveletigénye a fokszámmal négyzetes arányban nő.
(B) Tetszőleges folytonos függvény gyökeinek meghatározására alkalmazható.
(C) Szélsőérték meghatározására is közvetlenül alkalmazható.
(D) Polinom deriváltjainak kiszámítására is alkalmazható.
(D) Polinom deriváltjainak kiszámítására is alkalmazható.
59
New cards
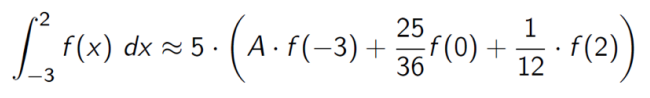
Tekintsük az ábrán látható kvadratúraformulát.
Hogyan válasszuk meg az A együttható értékét, hogy interpolációs kvadratúraformulát kapjunk?
\
(A) A = 2/3.
(B) A = 0.
(C) A = 2/9.
(D) A = 9/2.
Hogyan válasszuk meg az A együttható értékét, hogy interpolációs kvadratúraformulát kapjunk?
\
(A) A = 2/3.
(B) A = 0.
(C) A = 2/9.
(D) A = 9/2.
(C) A = 2/9.
60
New cards
Legyen x és y két egymáshoz közeli, hibával terhelt mennyiség. Az alábbi összefüggések közül melyik igaz?
(A) δx+y magas.
(B) δx−y magas.
(C) ∆x+y magas.
(D) ∆x−y magas.
(A) δx+y magas.
(B) δx−y magas.
(C) ∆x+y magas.
(D) ∆x−y magas.
(B) δx−y magas.
61
New cards

(A)
62
New cards

(A)
63
New cards
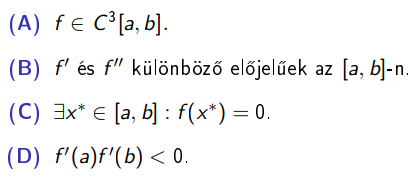
Az f (x) = 0 egyenlet megoldásához Newton-módszert szeretnénk használni. Melyik feltétel teljesülése esetén lehetünk biztosak abban, hogy a monoton konvergencia tétel **nem** alkalmazható?
(D)
64
New cards
Az alábbiak közül melyik tanult tétel garantálja a legmagasabb rendű konvergenciát?
\
(A) Húrmódszer konvergenciatétele.
(B) Banach-féle fixponttétel.
(C) Newton módszer monoton konvergenciája.
(D) Mindegyik csak 1-rendű konvergenciát igényel.
\
(A) Húrmódszer konvergenciatétele.
(B) Banach-féle fixponttétel.
(C) Newton módszer monoton konvergenciája.
(D) Mindegyik csak 1-rendű konvergenciát igényel.
(D) Mindegyik csak 1-rendű konvergenciát igényel.
65
New cards
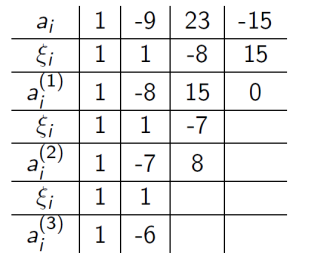
Az alábbi, P értékeire vonatkozó Horner-algoritmusból adódó táblázat alapján mi lesz ( Q(3) + 1/2) P’’(1) értéke, ahol P(x) = Q(x)(x-1)?
\
(A) -6.
(B) 6
(C) -3
(D) 3
\
(A) -6.
(B) 6
(C) -3
(D) 3
(A) -6.
66
New cards
Tegyük fel, hogy az A ∈ Rⁿˣⁿ mátrix rendelkezik az alábbi tulajdonságokkal:
* zᵀ Az > 0 minden Z ∈ Rⁿ, z ≠ 0 vektorra.
* aᵢ,ⱼ = aⱼ,ᵢ (i, j = 1,…..,n).
Az A mátrix LLᵀ felbontása ekkor
\
(A) Nem létezik.
(B) Egyértelműen létezik.
(C) Nincs elegendő információnk ahhoz, hogy a Cholesky-felbontás létezését megállapítsuk.
* zᵀ Az > 0 minden Z ∈ Rⁿ, z ≠ 0 vektorra.
* aᵢ,ⱼ = aⱼ,ᵢ (i, j = 1,…..,n).
Az A mátrix LLᵀ felbontása ekkor
\
(A) Nem létezik.
(B) Egyértelműen létezik.
(C) Nincs elegendő információnk ahhoz, hogy a Cholesky-felbontás létezését megállapítsuk.
(B) Egyértelműen létezik.
67
New cards
Melyik állítás **nem** teljesül minden H = H(v) ∈ Rⁿˣⁿ Householder-mátrixra?
\
(A) H(v)v = v
(B) H(-v)v = -v
(C) H(v)v = -v
(D) H(-v)(-v) = v
\
(A) H(v)v = v
(B) H(-v)v = -v
(C) H(v)v = -v
(D) H(-v)(-v) = v
(A) H(v)v = v
68
New cards
Tegyük fel, hogy az A mátrix **______**, és az Ax = b LER-re felírt Jacobi-iteráció konvergens tetszőleges x⁽⁰⁾ esetén. Mit írjunk **______** helyére, hogy a Gauss-Seidel módszer biztosan kétszer gyorsabban tartson a megoldáshoz?
\
(A) pozitív definit
(B) szigorúan diagonálisan domináns a soraira nézve
(C) tridiagonális
(D) negatív definit
\
(A) pozitív definit
(B) szigorúan diagonálisan domináns a soraira nézve
(C) tridiagonális
(D) negatív definit
(C) tridiagonális
69
New cards
Az alapműveletek hibakorlátaira vonatkozó ismereteink szerint mely állítás igaz?
\
(A) A nagy pozitív számmal való osztás nagy mértékben növeli az eredmény abszolút hibakorlátját.
(B) A nagy pozitív számmal való osztás nagy mértékben növeli az eredmény relatív hibakorlátját.
(C) Két kicsi pozitív szám összeadása nagy mértékben növeli az eredmény abszolút hibakorlátját.
(D) Két kicsi pozitív szám összeadása nagy mértékben növeli az eredmény relatív hibakorlátját.
\
(A) A nagy pozitív számmal való osztás nagy mértékben növeli az eredmény abszolút hibakorlátját.
(B) A nagy pozitív számmal való osztás nagy mértékben növeli az eredmény relatív hibakorlátját.
(C) Két kicsi pozitív szám összeadása nagy mértékben növeli az eredmény abszolút hibakorlátját.
(D) Két kicsi pozitív szám összeadása nagy mértékben növeli az eredmény relatív hibakorlátját.
(D) Két kicsi pozitív szám összeadása nagy mértékben növeli az eredmény relatív hibakorlátját.
70
New cards
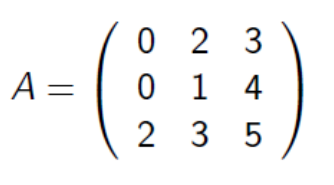
Tekintsük az alábbi mátrixot. A következő állítások közül melyik igaz?
\
(A) A főátlóban 0 van, ezért a mátrix determinánsa 0.
(B) A Gauss-elimináció nem hajtható végre sor- és oszlopcsere nélkül.
(C) A Gauss-elimináció végrehajtható sor- és oszlopcsere nélkül.
(D) A Gauss-elimináció egyik változata sem hajtható végre.
\
(A) A főátlóban 0 van, ezért a mátrix determinánsa 0.
(B) A Gauss-elimináció nem hajtható végre sor- és oszlopcsere nélkül.
(C) A Gauss-elimináció végrehajtható sor- és oszlopcsere nélkül.
(D) A Gauss-elimináció egyik változata sem hajtható végre.
(B) A Gauss-elimináció nem hajtható végre sor- és oszlopcsere nélkül.
71
New cards
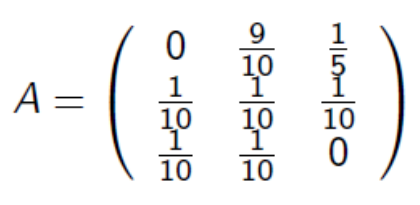
Tekintsük az alábbi mátrixot. Konvergens-e az A-ra felírt GS(1) iteráció?
\
(A) Nem, mert ||A||∞ > 1.
(B) Igen, mert ||A||₂ < 1.
(C) Igen, mert ρ(A) < 1
(D) Nem, mert A-hoz nem létezik Bgs₍₁₎
\
(A) Nem, mert ||A||∞ > 1.
(B) Igen, mert ||A||₂ < 1.
(C) Igen, mert ρ(A) < 1
(D) Nem, mert A-hoz nem létezik Bgs₍₁₎
(D) Nem, mert A-hoz nem létezik Bgs₍₁₎
72
New cards
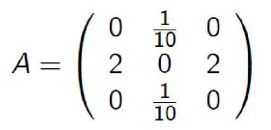
Tekintsük az alábbi mátrixot. Konvergens-e az A-ra felírt J(1) iteráció?
\
(A) Igen, mert ||A||∞ > 1.
(B) Nem, mert ||A||₂ < 1.
(C) Igen, mert ρ(A) < 1
(D) Nem, mert A-hoz nem létezik BJ₍₁₎
\
(A) Igen, mert ||A||∞ > 1.
(B) Nem, mert ||A||₂ < 1.
(C) Igen, mert ρ(A) < 1
(D) Nem, mert A-hoz nem létezik BJ₍₁₎
(D) Nem, mert A-hoz nem létezik BJ₍₁₎
73
New cards
Tegyük fel, hogy az A ∈ Rⁿˣⁿ mátrixon a Gauss-elimináció végrehajtása sikerült, és ezután
aₙ,ₙ⁽ⁿ⁻¹⁾ = 0 eredményre jutottunk. Mit jelent ez?
(A) A Gauss-elimináció során legalább egyszer sort- vagy oszlopot kellett cserélnünk.
(B) Az A mátrixhoz tartozó lineáris egyenletrendszernek nincs megoldása.
(C) A-nak nem létezik az LU felbontása.
(D) Az A mátrixhoz tartozó lineáris egyenletrendszer megoldásvektorának utolsó komponenense tetszőleges.
aₙ,ₙ⁽ⁿ⁻¹⁾ = 0 eredményre jutottunk. Mit jelent ez?
(A) A Gauss-elimináció során legalább egyszer sort- vagy oszlopot kellett cserélnünk.
(B) Az A mátrixhoz tartozó lineáris egyenletrendszernek nincs megoldása.
(C) A-nak nem létezik az LU felbontása.
(D) Az A mátrixhoz tartozó lineáris egyenletrendszer megoldásvektorának utolsó komponenense tetszőleges.
(C) A-nak nem létezik az LU felbontása.
74
New cards
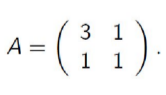
Az ábrán látható mátrix esetén:
\
(A) cond₂(A) = cond₂(R), ahol R az A mátrix OR-felbontásából származik.
(B) cond₂(A) = cond₂(Q), ahol Q az A mátrix QR-felbontásából származik.
(C) cond₂(A) = cond₂(L), ahol L az A mátrix LU-felbontásából származik.
(D) cond₂(A) = cond₂(L), ahol L az A mátrix LLᵀ -felbontásából származik.
\
(A) cond₂(A) = cond₂(R), ahol R az A mátrix OR-felbontásából származik.
(B) cond₂(A) = cond₂(Q), ahol Q az A mátrix QR-felbontásából származik.
(C) cond₂(A) = cond₂(L), ahol L az A mátrix LU-felbontásából származik.
(D) cond₂(A) = cond₂(L), ahol L az A mátrix LLᵀ -felbontásából származik.
(A) cond₂(A) = cond₂(R), ahol R az A mátrix QR-felbontásából származik.
75
New cards

(D)
76
New cards
Az M := M(t, k-, k+), ahol k- = -1k+ gépi számhalmazra vonatkozó állítások közül melyik teljesül minden esetben?
(A) ε0 < ε1
(B) ∀x ∈ M : x ≥ ε0
(C) |M| > 1 => ε0ε1 ≤ M∞
(D) M∞ \*ε0 / 2 > ε1
(A) ε0 < ε1
(B) ∀x ∈ M : x ≥ ε0
(C) |M| > 1 => ε0ε1 ≤ M∞
(D) M∞ \*ε0 / 2 > ε1
C) |M| > 1 => ε0ε1 ≤ M∞
77
New cards
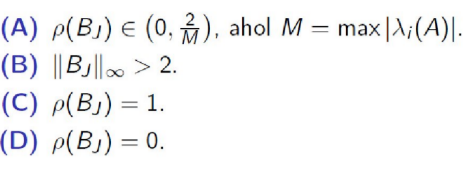
Tegyük fel, hogy egy adott LER mátrixa tridiagonális, szimmetrikus, és pozitív definit, valamint a relaxált Gauss-Seidel iterációhoz tartozó optimális paraméter ωopt = 1.
Mit mondhatunk ekkor a LER-re felírt Jacobi-iteráció iterációs mátrixáról?
\
Mit mondhatunk ekkor a LER-re felírt Jacobi-iteráció iterációs mátrixáról?
\
(D)
78
New cards
Az ILU iteráció B_ILU = P⁻¹Q átmenetmátrixára melyik teljesül?
(A) Ha Q a LER A mátrixához közelít, akkor az iteráció gyors lesz.
(B) Ha P⁻¹ az A mátrixhoz közeli, akkor az iteráció gyors lesz.
(C) Ha P az A mátrixhoz közeli, akkor az iteráció gyors lesz.
(D) Ha Q⁻¹ az A mátrixhoz közeli, akkor az iteráció gyors lesz.
(A) Ha Q a LER A mátrixához közelít, akkor az iteráció gyors lesz.
(B) Ha P⁻¹ az A mátrixhoz közeli, akkor az iteráció gyors lesz.
(C) Ha P az A mátrixhoz közeli, akkor az iteráció gyors lesz.
(D) Ha Q⁻¹ az A mátrixhoz közeli, akkor az iteráció gyors lesz.
(C) Ha P az A mátrixhoz közeli, akkor az iteráció gyors lesz.
79
New cards
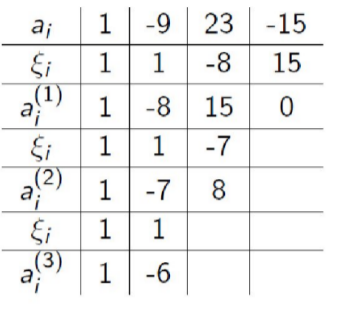
Az alábbi, P értékeire vonatkozó Horner-algoritmusból adódó táblázat alapján mi lesz Q(4)\*P’’(1) értéke, ahol P(x) = Q(x)(x - 1)?
\
(A) 12
(B) -12
(C) 8
(D) -8
\
(A) 12
(B) -12
(C) 8
(D) -8
(A) 12
80
New cards
Az A ∈ R⁴ˣ⁴ szimmetrikus mátrix sajátértékei -2,3,4,6. Melyik állítás igaz az alábbiak közül?
\
(A) cond(A) ≥ 3
(B) cond₂(A) = -3
(C) cond(A) ≤ 3
(D) Nem biztos, hogy A invertálható és létezik kondíciószáma.
\
(A) cond(A) ≥ 3
(B) cond₂(A) = -3
(C) cond(A) ≤ 3
(D) Nem biztos, hogy A invertálható és létezik kondíciószáma.
A) cond(A) ≥ 3
81
New cards
Az A ∈ R⁴ˣ⁴ szimmetrikus mátrix sajátértékei -2,1,2,4. Melyik állítás igaz az alábbiak közül?
\
(A) cond₂(A) = 4
(B) cond₂(A) = 2
(C) cond(A) ≥ 4
(D) Nem biztos, hogy A invertálható és létezik kondíciószáma.
\
(A) cond₂(A) = 4
(B) cond₂(A) = 2
(C) cond(A) ≥ 4
(D) Nem biztos, hogy A invertálható és létezik kondíciószáma.
(C) cond(A) ≥ 4
82
New cards
Melyik vektornorma-mátrixnorma pár illeszkedő az alábbiak közül?
\
(A) || . ||₂ vektornorma és || . ||F mátrixnorma.
(B) || . ||₂ vektornorma és || . ||ᵤ,
ahol ||B||ᵤ := sqrt(tr(BᵀB))
(C) Mindkettő.
(D) Egyik sem.
\
(A) || . ||₂ vektornorma és || . ||F mátrixnorma.
(B) || . ||₂ vektornorma és || . ||ᵤ,
ahol ||B||ᵤ := sqrt(tr(BᵀB))
(C) Mindkettő.
(D) Egyik sem.
(C) Mindkettő.
83
New cards
Tegyük fel, hogy az x ∈ Rₘ szám fl(x) ∈ M(7, -16, 16) gépi számhalmazbéli alakjának karakterisztikája 10.
Melyik **nem** relatív hibakorlátja az ábrázolt számnak?
(A) 2⁻⁷
(B) 2⁻⁶
(C) 2⁻⁸
(D) 2⁻⁵
Melyik **nem** relatív hibakorlátja az ábrázolt számnak?
(A) 2⁻⁷
(B) 2⁻⁶
(C) 2⁻⁸
(D) 2⁻⁵
(C) 2⁻⁸
84
New cards
Tegyük fel, hogy az x ∈ Rₘ szám fl(x) ∈ M(8, -16, 16) gépi számhalmazbéli alakjának karakterisztikája 10.
Melyik **nem** relatív hibakorlátja az ábrázolt számnak?
(A) 2⁻⁶
(B) 2⁻⁷
(C) 2⁻⁸
(D) 2⁻⁹
Melyik **nem** relatív hibakorlátja az ábrázolt számnak?
(A) 2⁻⁶
(B) 2⁻⁷
(C) 2⁻⁸
(D) 2⁻⁹
D) 2⁻⁹
85
New cards
Tegyük fel, hogy az x ∈ Rₘ szám fl(x) ∈ M(8, -16, 16) gépi számhalmazbéli alakjának karakterisztikája 11.
Mit mondhatunk az ábrázolásból eredő hibakorlátról? Melyik az a legkisebb egész szám, amivel biztosan felülről tudjuk becsülni az ábrázolás hibáját? lx — fI(x)I < ?
\
(A) 8
(B) 4
(C) 2
(D) 1
Mit mondhatunk az ábrázolásból eredő hibakorlátról? Melyik az a legkisebb egész szám, amivel biztosan felülről tudjuk becsülni az ábrázolás hibáját? lx — fI(x)I < ?
\
(A) 8
(B) 4
(C) 2
(D) 1
(B) 4
86
New cards
Milyen rendben konvergál az xₖ₊₁ = xₖ - sin(xₖ), x₀ = 1
fixpont-iteráció?
\
(A) Negyedrendű
(B) Harmadrendű
(C) Másodrendű
(D) Elsőrendű
fixpont-iteráció?
\
(A) Negyedrendű
(B) Harmadrendű
(C) Másodrendű
(D) Elsőrendű
(B) Harmadrendű
87
New cards
Legyen a,b ∈ Rⁿ, a ≠ b ≠ 0, ||a-b||₂ = 1, és aᵀa = bᵀb.
Ekkor a v = a-b vektorra:
\
(A) H(v)a = a.
(B) H(v)a = b.
(C) H(a)v = -v.
(D) H(v)b = -b.
Ekkor a v = a-b vektorra:
\
(A) H(v)a = a.
(B) H(v)a = b.
(C) H(a)v = -v.
(D) H(v)b = -b.
(B) H(v)a = b.
88
New cards
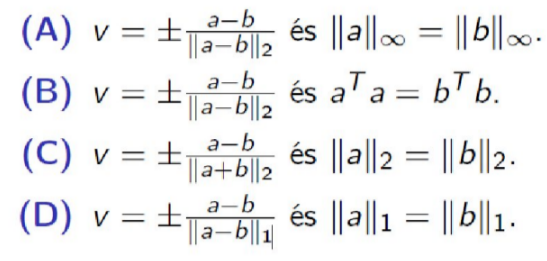
Legyen a,b ∈ Rⁿ, a ≠ b ≠ 0. Ekkora H(v)a = b teljesül, ha
\
\
(B)
89
New cards
Legyen Bⱼ ∈ Rⁿˣⁿ egy Jacobi-iteráció átmenetmátrixa, λᵢ ∈ R, vᵢ ∈ Rⁿ olyan, hogy
Bⱼᵥᵢ = λᵢ vᵢ (i = 1,….,n).
Jelölje továbbá Bⱼ(ω) az ω ∈ (0,1) paraméterű csillapított Jacobi-iteráció átmenetmátrixát. Ekkor:
\
(A) Bⱼᵥᵢ = ((1-ω)l + ωBⱼ)vᵢ
(B) Bⱼ(ω)ᵥᵢ = ((1-ω)l + ωBⱼ)λᵢ
(C) Bⱼ(ω)ᵥᵢ = ((1-ω)l + ωBⱼ)vᵢ
(D) Bⱼ(ω)ᵥᵢ = ((1-λᵢ)l + λᵢBⱼ)vᵢ
Bⱼᵥᵢ = λᵢ vᵢ (i = 1,….,n).
Jelölje továbbá Bⱼ(ω) az ω ∈ (0,1) paraméterű csillapított Jacobi-iteráció átmenetmátrixát. Ekkor:
\
(A) Bⱼᵥᵢ = ((1-ω)l + ωBⱼ)vᵢ
(B) Bⱼ(ω)ᵥᵢ = ((1-ω)l + ωBⱼ)λᵢ
(C) Bⱼ(ω)ᵥᵢ = ((1-ω)l + ωBⱼ)vᵢ
(D) Bⱼ(ω)ᵥᵢ = ((1-λᵢ)l + λᵢBⱼ)vᵢ
(C) Bⱼ(ω)ᵥᵢ = ((1-ω)l + ωBⱼ)vᵢ
90
New cards
Legyen t ∈ N+ és tekintsük az M(t, t, t) gépi számhalmazt! Milyen t-re teljesül, hogy
|M| - M∞ < ε₀
\
(A) t < 2
(B) t > 2
(C) t = 2
(D) Minden lehetséges t-re teljesül a feltétel.
|M| - M∞ < ε₀
\
(A) t < 2
(B) t > 2
(C) t = 2
(D) Minden lehetséges t-re teljesül a feltétel.
(B) t > 2
91
New cards
Tegyük fel, hogy az A ∈ Rⁿˣⁿ szimmetrikus mátrixnak egyértelműen létezik LLᵀ - felbontása. Melyik állítás nem igaz az alábbiak közül?
\
(A) cond₂(A) ≥ cond₂(L)
(B) cond₂(det(A) \* A) = cond₂(L)²
(C) cond₂(A)² = cond₂(Lᵀ)
(D) cond_F(A) ≥ cond₂(L)
\
(A) cond₂(A) ≥ cond₂(L)
(B) cond₂(det(A) \* A) = cond₂(L)²
(C) cond₂(A)² = cond₂(Lᵀ)
(D) cond_F(A) ≥ cond₂(L)
(B) cond₂(det(A) \* A) = cond₂(L)²
92
New cards
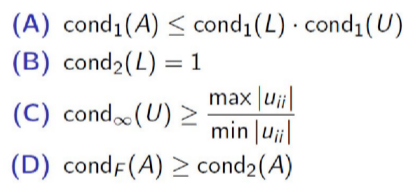
Tegyük fel, hogy az A ∈ Rⁿˣⁿ mátrixnak egyértelműen létezik LU-felbontása. Melyik állítás nem igaz az alábbiak közül?
\
\
(B)
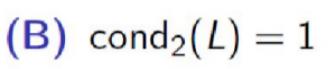
93
New cards
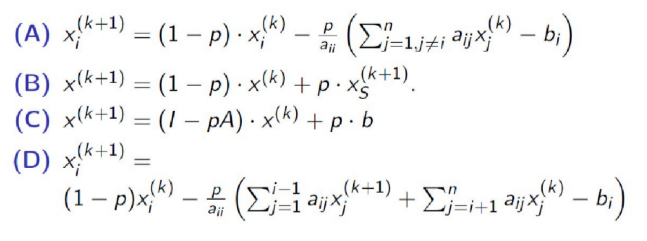
Melyik igaz a csillapított Gauss-Seidel iteráció által adott k - 1-ik közelítő eredményre?
\
\
(D)
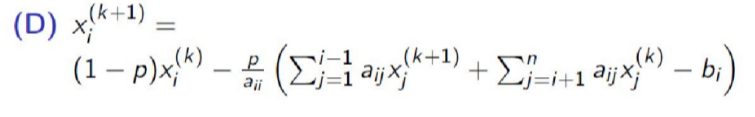
94
New cards
Mindig létezik-e olyan x ≠ 0 vektor, ami az
||Ax||₂ / ||x||₂ hányadost minimalizálja?
\
(A) Igen, λₘᵢₙ(A) sajátérték egy sajátvektora mindig ilyen.
(B) Igen, λₘᵢₙ(A⁻¹AᵀA) sajátérték egy sajátvektora mindig ilyen.
(C) Igen, λₘᵢₙ(AAᵀ) sajátérték egy sajátvektora mindig ilyen.
(D) Nem létezik minimum, csak az inf létezése garantált.
||Ax||₂ / ||x||₂ hányadost minimalizálja?
\
(A) Igen, λₘᵢₙ(A) sajátérték egy sajátvektora mindig ilyen.
(B) Igen, λₘᵢₙ(A⁻¹AᵀA) sajátérték egy sajátvektora mindig ilyen.
(C) Igen, λₘᵢₙ(AAᵀ) sajátérték egy sajátvektora mindig ilyen.
(D) Nem létezik minimum, csak az inf létezése garantált.
(C) Igen, λₘᵢₙ(AAᵀ) sajátérték egy sajátvektora mindig ilyen.
95
New cards
Melyik mátrixnorma indukált az alábbiak közül?
\
(A) ||.||₁
(B) ||.||∞
(C) Mindkét mátrixnorma indukált.
(D) Egyik sem indukált
\
(A) ||.||₁
(B) ||.||∞
(C) Mindkét mátrixnorma indukált.
(D) Egyik sem indukált
(C) Mindkét mátrixnorma indukált.
96
New cards
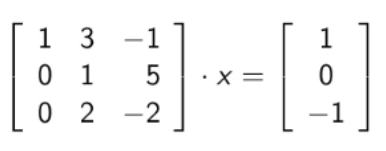
Az alábbi lineáris egyenletrendszer megoldását Gauss-elimináció és részleges főkiválasztás használatával szeretnénk meghatározni. Mit tesz az algoritmusunk a Gauss-elimináció második lépésének végrehajtását megelőzően?
\
(A) Semmit, elvégzi a Gauss-elimináció második lépését.
(B) Kicseréli a 2. és a 3. sort.
(C) Kicseréli a 2. és az 1. sort.
(D) Kicseréli a 2. és a 3. oszlopot.
\
(A) Semmit, elvégzi a Gauss-elimináció második lépését.
(B) Kicseréli a 2. és a 3. sort.
(C) Kicseréli a 2. és az 1. sort.
(D) Kicseréli a 2. és a 3. oszlopot.
(B) Kicseréli a 2. és a 3. sort.
97
New cards
Legyen x és y két hibával terhelt mennyiség. Az alábbi összefüggések közül melyik **hamis**?
\
(A) δₓᵧ = δₓ + δᵧ
(B) δₓ/ᵧ = δₓ + δᵧ
(C) △ₓ₊ᵧ = △ₓ + △ᵧ
(D) △ₓ₋ᵧ = △ₓ - △ᵧ
\
(A) δₓᵧ = δₓ + δᵧ
(B) δₓ/ᵧ = δₓ + δᵧ
(C) △ₓ₊ᵧ = △ₓ + △ᵧ
(D) △ₓ₋ᵧ = △ₓ - △ᵧ
(D) △ₓ₋ᵧ = △ₓ - △ᵧ
98
New cards
Tegyük fel, hogy egy interpolációs feladatban szereplő ω₃ polinom a következő alakú:
ω₃(x) = (x+1)(x-1)(x-2)(x-3). Az alábbiak közül melyik lehet az ℓ₁(x) Lagrange-alappolinom?
\
(A) (x+1)(x-2)(x-3) / 3
(B) (x+1)(x-2)(x-3) / -3
(C) (x+1)(x-2)(x-3) / 4
(D) (x+1)(x-2)(x-3) / -4
ω₃(x) = (x+1)(x-1)(x-2)(x-3). Az alábbiak közül melyik lehet az ℓ₁(x) Lagrange-alappolinom?
\
(A) (x+1)(x-2)(x-3) / 3
(B) (x+1)(x-2)(x-3) / -3
(C) (x+1)(x-2)(x-3) / 4
(D) (x+1)(x-2)(x-3) / -4
(C) (x+1)(x-2)(x-3) / 4
99
New cards
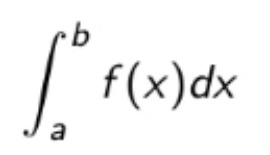
A képen látható határozott integrál értékét az E(f) érintőformulával szeretnénk közelíteni. Válassza ki a helyes képletet!
\
(A) E(f) = (b-a) \* f((b+a)/2)
(B) E(f) = ((b-a)/2) \* f((b+a)/2)
(C) E(f) = (b+a) \* f((b-a)/2)
(D) E(f) = ((b+a)/2) \* f((b-a)/2)
\
(A) E(f) = (b-a) \* f((b+a)/2)
(B) E(f) = ((b-a)/2) \* f((b+a)/2)
(C) E(f) = (b+a) \* f((b-a)/2)
(D) E(f) = ((b+a)/2) \* f((b-a)/2)
(A) E(f) = (b-a) \* f((b+a)/2)
100
New cards
Az f(x) = 0 egyenlet megoldásához Newton-módszert szeretnénk használni. Az erre vonatkozó tétel alapján a módszer monoton konvergenciájához az alábbi feltételek közül melyik nem szükséges?
\
(A) f ∈ C²\[a,b\]
(B) f’ állandó előjelű az \[a,b\]-n.
(C) f’’ nem vált előjelet az \[a,b\]-n.
(D) f’ és f’’ előjele megegyezik az \[a,b\]-n.
\
(A) f ∈ C²\[a,b\]
(B) f’ állandó előjelű az \[a,b\]-n.
(C) f’’ nem vált előjelet az \[a,b\]-n.
(D) f’ és f’’ előjele megegyezik az \[a,b\]-n.
(D) f’ és f’’ előjele megegyezik az \[a,b\]-n.