5.1, Exponential Functions

This is when a and b are real numbers, B is greater than 0 but doesn’t equal 1. This is expressed as f(x)= a(b^x)

What is an Exponential Function?

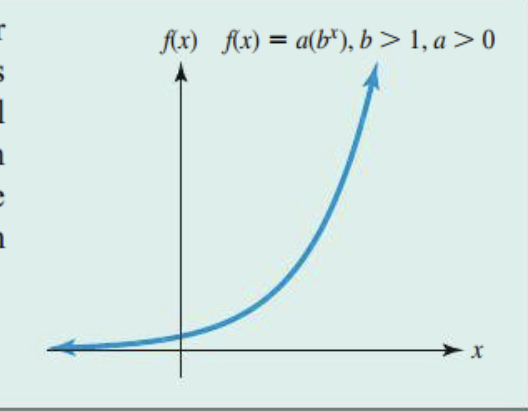
This is an Exponential Function where the base, “b” is greater than 1 and a is greater than 0. The growth factor is increasing.

• X-intercept: None

• Y-intercept: (0,a) whatever a is

• Domain (negative infinity, infinity)

• Range (0, infinity)

• Horizontal Asymptote: X-axis/ Y=0

• Shape: Increasing, concaving up

What is an Exponential Growth Function?

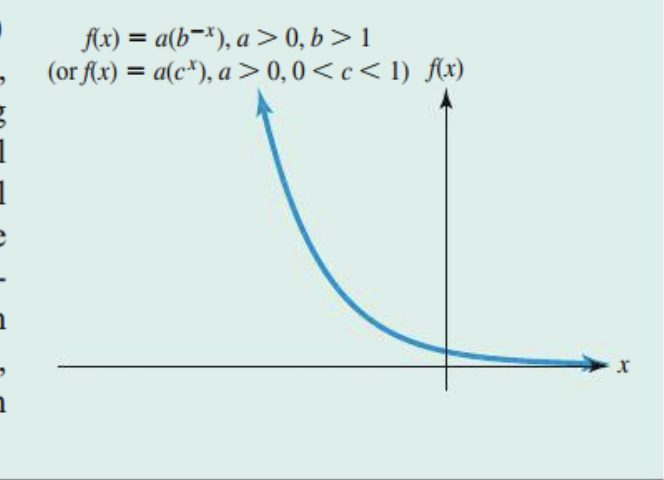
This is an Exponential Function where “b” is greater than 1 and “a” is greater than zero; HOWEVER, ‘k’ is LESS than Zero.

• X-intercept: None

• Y-intercept: (0,a) whatever a is

• Domain: (Negative infinity, infinity)

• Range (0, infinity)

• Horizontal Asymptote: X-axis/ Y=0

• Shape: Decreasing, concaving up

What is an Exponential Decay Function?

This formula is continuously compounding. That means a future investment is earning money every moment of every day.

What is S=Pe^rt

This formula is without an “e” is compounding a certain number of times throughout a year. “Compounding annually.”

What is S=P(1+r)^t

Describe what’s happening with the value “k”: g(x) = b^x +k

"k" is positive, meaning a vertical shift upwards of the exponential function.

Describe what’s happening with the value “k”: g(x)=b^x-k

"k" is negative, the graph shifts downward vertically,

Describe what’s happening with the value of “h”: g(x)=b^x-h

“h” is negative, meaning the graph horizontally shifts left

Describe what’s happening with the value of “h”: g(x)=b^x+h

“h” is positive, indicating a horizontal shift to the right.

Describe what’s happening: g(x)= -b^x

The base: “b” is negative, indicating a reflection across the x-axis

Describe what’s happening: g(x)= b^-x

The exponent: “x” is negative, indicating a reflection across the y-axis

Describe what’s happening: g(x)= 2 times b^x

The |a| is greater than 1, meaning the graph is vertically stretched

Describe what’s happening: g(x)= 0.1 times b^x

The |a| is less than 1, meaning the graph is vertically compressed

Describe what’s happening: b²^times x

The |a|= 2, greater than 1, meaning the graph is horizontally compressed

During a 20-year period of constant inflation, the value of a $150,000 property will increase according to the equation v=150,000e^0.04t.

• What will the value of the property be in 6 years?

S=Pe^rt → S=150,000e^0.04(6)

= $190,687.37

During a 20-year period of constant inflation, the value of a $150,000 property will increase according to the equation v=150,000e^0.04t.

• When will this property be worth double its original value?

$150,000 → $300,000

• y1= 150,000e^0.04t

• y2= 300,000

• Find where they intersect

= Around 17.3 years.