MATHS - Ju + J (Yr12 stats)

what are the mathematical sampling methods

Common methods include:

random sampling

stratified sampling

cluster sampling

systematic sampling

quota sampling

what is quota sampling

Quota sampling is a non-probability sampling method where researchers ensure equal representation of different subgroups by setting quotas for each category, based on specific characteristics like age, gender, or income.

what is cluster sampling

Cluster sampling is a probability sampling method where the population is divided into clusters, usually geographically, and entire clusters are randomly selected for inclusion in the sample.

groups of convenience over relevant factors.

strengths of each sampling method

strengths:

random sampling reduces bias and increases generalizability

stratified sampling ensures representation of subgroups

cluster sampling is cost-effective for large populations

systematic sampling simplifies the selection process

quota sampling allows for demographic representation without randomization.

limitations of each sampling methods

Limitations include:

random sampling can be impractical for large groups

stratified sampling may require detailed population data

cluster sampling might introduce sampling error if clusters are not homogeneous

systematic sampling can lead to bias if there is an unseen pattern

quota sampling lacks randomness, which can affect representativeness.

what are the conditions that are needed for binomial distribution to be helpful

• number of trials is fixed

• each outcome is either success or failure

• the trials are independent of each other

• probability of success is the same in each trial

what is the eq. for binomial distribution and what do the symbols stand for

The equation for binomial distribution is

• ( P(X = k) = \binom{n}{k} p^k (1-p)^{n-k} ),

where

• ( n ) is the number of trials

• ( k ) is the number of successes

• ( p ) is the probability of success

• ( \binom{n}{k} ) is the binomial coefficient.

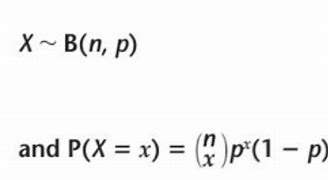
what are the steps one the calculator for solving binomial distribution

stats - dist - binomial - Bpd

Bpd - fixed no.

Bcd - cumulative

IvB - inverse (don’t need now)

what is the formula for binomial distribution

P(X=x) = nCx p^x (1-p)^{n-x}

what are the equations for variance and mean given that X - B(n,p)

mean = np

Variance = np(1-p)

what is the order of values when using Binomial distribution in run

(x,n,p)

what is the null hypothesis

The null hypothesis is a statement used in statistical testing that indicates no effect or no difference in a given context.

denoted as H0.

what is the alternative hypothesis

The alternative hypothesis is a statement used in statistical testing that indicates there is an effect or a difference in a given context.

denoted as H1

what is a significance level

The significance level is the probability of rejecting the null hypothesis when it is true, typically denoted by alpha (α). It is used to determine the threshold for statistical significance in hypothesis testing.

a cut off number

what are the steps to determining whether a statistical hypothesis should be rejected or not

1. state the H0 and H1 and determine the value of P

2. find the probability of the suggested occurrence in your sample happening

3. compare this to your significance level

   • if Prob. < sig, level is too small the H0 is rejected

   • if Prob. > sig. level this is accepted

what are one tailed tests

when P is either < or > something

what are two tailed tests

when P does not = something

how do you calculate one tailed tests

if P > something

• calculate P(X>/=__)

if P < something

• calculate P(X</=__)

how do you calculate two tailed tests

1. half the sig, level OR double the probability

2. calculate the proportion of from the sample and compare with P.

3. if P > something

   • calculate P(X>/=__)

   if P < something

   • calculate P(X</=__)

what is meant by a critical region

a region in which the H0 would be rejected.

choose the value for n that is the closest to the significance level w/o exceeding it.