L8: Game Theory 1

Game Theory in real life

Game theoretical computer models have helped to predict:

• The successors of dictators

• Where we could find Osama Bin Laden

• Which leaders would fall from power

• Have brought insides when it comes to negotiations within the EU

• Have led to knowledge about vote trading in EU institutions

• Are used in auctions

• Have helped to decide when to set up a company (and where) and gives insights in the current market

Game

"A competitive activity... in which players contend with each other according to a set of rules"

Game theory

“A formal representation of a situation in which a number of individuals interact in a setting of strategic interdependence"

What is game theory?

• Formal study of strategic interactions

• It is the study of how we mathematically determine the
  best strategy given conditions to optimize the outcome

  • How do we get the most utility?

• It helps to analyze situations more rational and formulate acceptable alternatives

  • What are people doing and how do we react?

• Everything can be considered a game (in a game theoretical sense)

• At least twelve (!!) game theorists have won the Nobel prize in economics so far....

History

• Game theoretical notions go back for hundreds of years

  • Talmud: dividing a dead man’s estate between three creditors

    • Robert Aumann and Micheal Maschler cracked the ‘code’

  • Sun Tzu’s writings: strategic warfare

• Modern game theory credited to John von Neumann

• John von Neumann and Oskar Morgenstern

  • Expected utility theory creators

• John Nash generalized these results and provided the basis of the modern field of game theory

What is a game?

• A set of players {A,B, C...}

• A set of strategies

• The payoff (i.e., what a player gets) is listed for each possible list of strategies of each player

  • Utility

Types of games

• Simultaneous vs Sequential games

  • Players move at the same time or the action of one depends of another

• Single play vs Iterated games

  • Games is played only once vs multi-stage games

• Zero vs positive sum games

  • The same of the payoff remain constant during the game vs they change

    • One winner vs we can win together

• Complete vs incomplete information games

  • Players know or do not know each others payoffs

    • Everything is known to every player vs not

• Non-cooperative vs cooperative games

  • Players can or cannot form binding agreements and coalitions

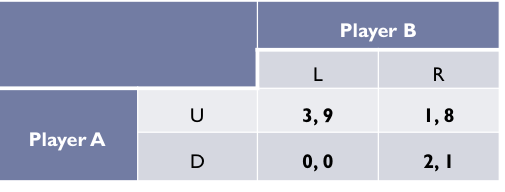
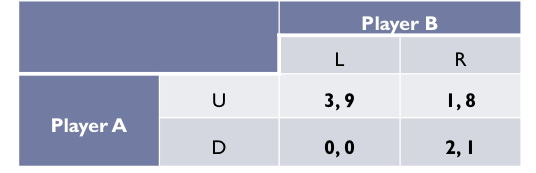
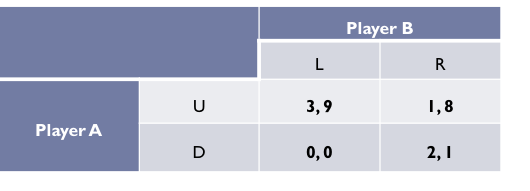
Example of two player game

• The players are called {A, B}

• Player A has two strategies: "Up" and "Down" {U,D}

• Player B has two strategies: "Left" and "Right" {L,R}

• These strategies are placed in a table together with the payoffs for both players for each of the four possible strategies

  • Payoffs = utility

• These tables are called payoff matrix (normal form games)

• For now, we focus on games with complete information: every player knows the payoffs of the other

Play

is a pair, such as (U,R) where the first element is the strategy chosen by Player A and the second is the strategy chosen by Player B

• A set of strategies → one for each player

Payoff matrix: which numbers should i compare?

If B plays left, the A has to decide between up and down —> choose between 3 and 0

• Higher number is the one you are more likely to play

If player A always chooses up, B needs to decide between left and right —> 9 or 8

• Compare the ones that have the same color

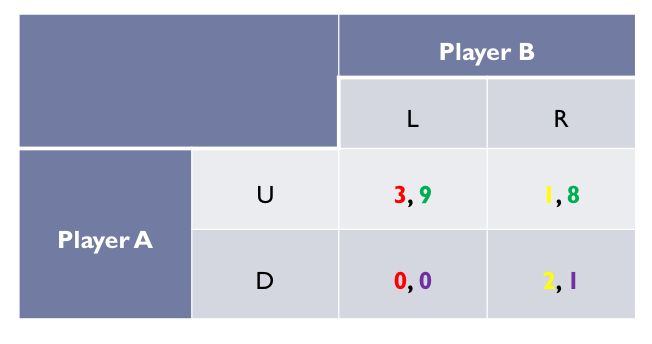
Which of the following plays are likely to occur?

U, R

D, R

D, L

U, L

U, R: no bc both players have incentive to deviate

D, R: yes bc they both gain more from staying than deviating → no incentive to change

D, L: no bc both players have incentive to deviate → more utility if change

U, L: yes bc both gain more by staying

What strategies are a Nash equilibrium?

U, L & D, R

John Forbes Nash

• Born in 1928 in Virginia

• Engineer at heart, chemistry, but ultimately mathematics

• His PhD thesis (Princeton) formulated the concept of Nash equilibrium

  • Now regarded as a basic building block of game theory!

• After defense, he produced several papers setting out several different theories

• In 1959: acute paranoid schizophrenia

  • Everyone accepted it → was able to work at Princeton

• From 1990 onward: progressive healing

• 1994: Nobel Prize in Economics

• 200l: A beautiful mind

• 2015: Abel prize and died in a car crash

Nash Equilibrium

• a set of strategies, one for each player, such that no player has incentives to change his or her strategy

  • One person deviating for a NE strategy would result in the same payout or lower payout for that person

  • It is the mutual best response

    • It is the happy place for both players 

• It is inherent stable!

Pure strategy Nash equilibrium PSNE

players only play a single strategy in equilibrium

• 100% play one strategy

• U, L and D, R are an example of PSNE

Mixed strategy Nash equilibrium MSNE

players play a combination of several strategies with a fixed probability ie they randomize between strategies

Nash equilibrium: problems

1. A game can have several Nash equilibria ((U,L) and (D, R) in our example) — so what is the outcome then?

   1.  —> different ways to argue which NE would be the best one

2. There may not be a Nash equilibrium in pure strategies

   1. Need mixed

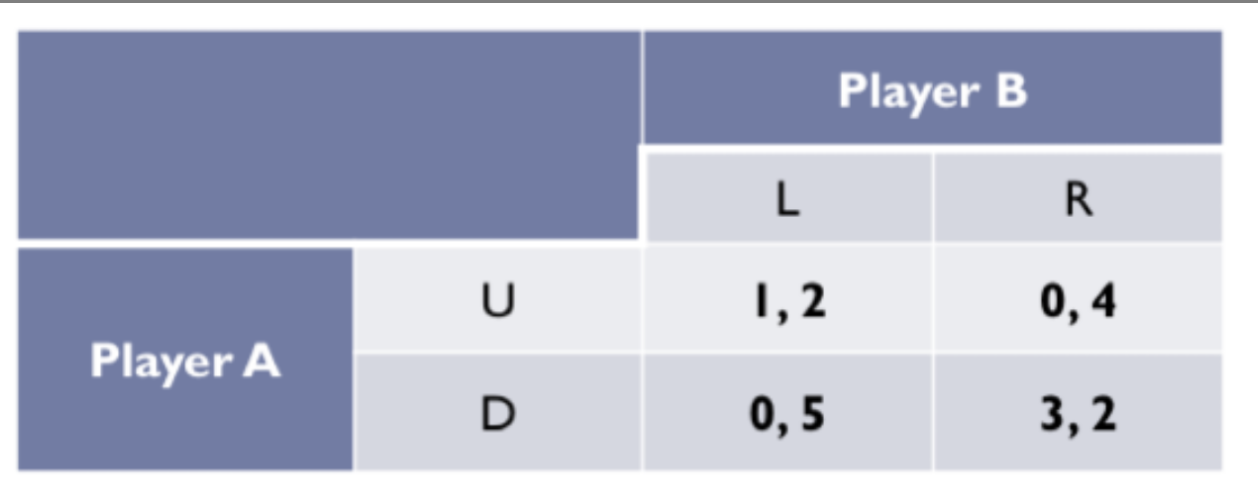
Are there any pure strategy Nash equilibrium?

No in each quarter, player A or B will want to deviate

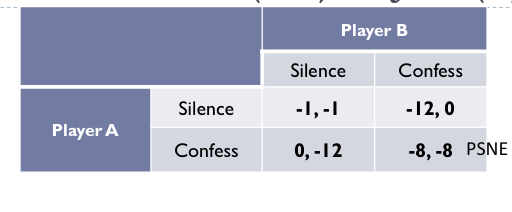
Prisoners Dilemma

• If no one confesses (Silence) for the robbery, the police can only charge the prisoners for trespassing

  • Punishment: I month in jail each

• If one confesses (Confess) and the other does not (Silence), the police will be lenient on the rat and severely punish the quiet one:

  • Punishment: 12 months in jail for the quiet one, 0 months for the rat

• If both confesses (Confess), the police will punish both equally

  • Punishment: 8 months in jail each

• Payoff:

  • Both stay silent both have an incentive to change to confess

Strictly dominant strategies

strictly dominates another strategy for a play if it generate a greater payoff regardless of what other players do

• Players never play strictly dominated strategies

• a strictly dominant strategy is that strategy that always provides greater utility to a player, no matter what the other player's strategy is;

• a weakly dominant strategy is that strategy that provides at least the same utility for all the other player's strategies, and strictly greater for some strategy 

Prisoners Dilemma NE

• The only Nash equilibrium (in pure strategies) for this game is (C, C), even though (S, S) gives both players better payoffs

• The only Nash equilibrium is so-called Pareto inefficient

Pareto inefficient

The outcome is suboptimal for both prisoners

Would the prisoners dilemma change if they were allowed to communicate with each other?

Even if they make a deal before they go to the interrogation room; this deal will not uphold because they have individual incentives to deviate from keeping silent

PD and reality

• PD games shows that even if there is a solution that makes both players better off, the rationality of players does not lead to it

  • Shows how difficult it is for people to cooperate

• Lack of communication is not the real problem but lack of trust! Even if they communicate, can they trust each other to hold onto the agreement?

  • Answer: no

• Does this scenario look familiar to you?

  • Looks like a collective action problem

• This property made this game a popular structure for modeling many political, economic, sociological, biological phenomena

• Examples?

  • Climate change policy

  • Arms race

• Even if cooperation is best for everyone, there is always incentive to deviate

Example of prisoners dilemma

• George Conway: Conservative lawyer (former republican)

  • Argues in a podcast called "Trump's 91 problems (& Jail is One)" that...

• "This has been the prisoner's dilemma problem of the Republican party... Nobody actually wants to go out and tell the truth about this guy because they don't want to be out there standing alone."

• Even though Republican senators would be better off fighting Trump's attack on democracy

  • They are not doing it, they are trapped

  • Is this really a PD game?

    • No be there is no incentive to switch - they are all staying silent and supporting Trump

Nash Equilibrium summary

• Technically, a Nash equilibrium is a set of strategies, one for each player, such that no player has incentive to change his or her strategy given what the other players are doing

• Practically speaking, a Nash equilibrium is a law that no one has incentive to break even in the absence of an effective police force. In a sense, these laws are self-enforcing

  • There can be multiple Nash equilibria in a game

  • There can also be no PSNE in a game

Stag Hunt game

• a game that describes a conflict between safety and social cooperation

• Also known as the "assurance game", "coordination game", and "trust dilemma"

• Some say that it better represents reality in comparison to PD games

• Principle: if people's actions complement each other, then getting a good outcome depends not just on what people value but on how they expect each other to behave

Stag hunt: background

• A group of hunters are on the hunt for stags

• If they work together, they can kill the stag, if not, the stag flee, and they will go hungry

• Stag is not easily found, while waiting they see a hare

Stag hunt: the game

• If a hunter leaps out and kills the hare, he will eat, but the trap laid for the stag will be wasted and the other hunters will starve

• There is no certainty that the stag will arrive; the hare is present

Stag hunt: dilemma

• If one hunter waits, his fellow hunter might kill the hare for himself, sacrificing everyone else

• This makes the risk twofold; the risk that the stag does not appear, and the risk that another hunter takes the kill

Stag hunt payoffs

• Highest pay-off (5,5) when both work together and kill the stag

• If one kills the rabbit he can eat (4), but another hunter has nothing

• If both work together and kill the rabbit they get (2,2)

• If hunter I picks Stag, best response is to also pick Stag over Hare (5>4)

• If hunter 2 picks Hare, it is more sensible to also pick Hare (2>0)

• Player I strategy is completely dependent on player's 2 choice and the other way around

• No strict dominant strategy

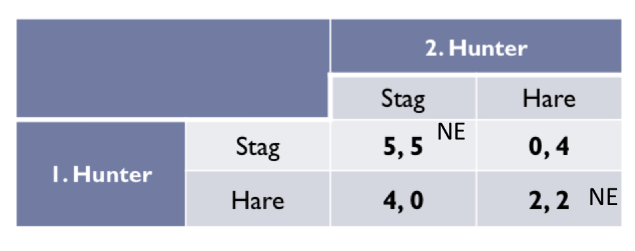
Stag hunt: focal point

Which one do you choose of the NE?

• 4, 4 is the better outcome as both players are happier

• Thomas schilling called this superior equilibrium

• Schilling argues it can be determined culturally or by communication

Stag hunt vs prisoners dilemma

• PD: despite cooperation is Pareto optimal outcome, the only PSNE is to defect

• SH: selfish incentives can produce social cooperation

Nash equilibriums are not always good or Pareto efficient; but they are stable!

Chicken game: principle

• It is an influential model of conflict escalation

• The principle of the game is that while it is preferable not to yield to the opponent, if neither player yields, this outcome is the worst possible one for both players

• It is a so-called 'anti-coordination game', in which it is mutually beneficial for the players to play different strategies

  • Also called hawk-dove game

Chicken game: story

• Two guys are at the opposite side of the road, pointing their cars to each other

• Driving right at each other

• Before they collide, they have to decide : risk a crash or swirl off to the side and risk reputation costs

Chicken game: payoff

• If both keep going, they might crash and die - so high negative payoffs (-100)

• If one keep going straight and the other swerve; the one that keeps going shows how tough, he is (positive utility: +2) and the other that he is a looser (negative payoffs: -2)

• If both swerve, not much will happen

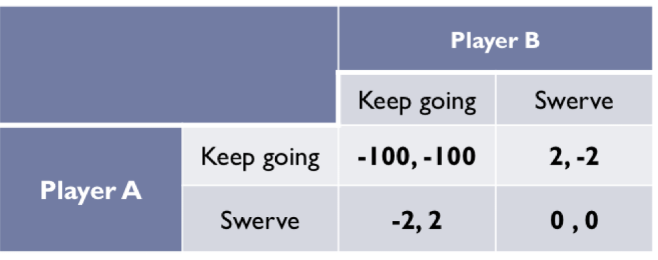
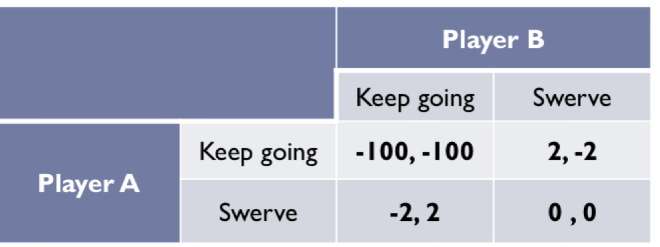
Chicken game: best response

1. (A: Keep Going, B: Swerve)

2. (A: Swerve, B: Keep Going)

Chicken game: problems

• how do we decide who is the one keep going and who is the one that swerves?

  • Is there any intuitive idea?

• We cannot enforce one of the two PSNE equilibrium

• A possible solution: Mixed Strategy Nash Equilibrium