Height of a tree (or a node) is the longest path from the root (or from the node) to a
leaf node
New cards
4
For BST: height = max (? ) + 1
left child’s height , right child’s height
New cards
5
The height of a NULL node is
\-1
New cards
6
leaf nodes have height
0
New cards
7
Use ? to determine if trees are imbalanced
balance factor
New cards
8
balance factor formula
hleft - hright
New cards
9
trees of both height can differ by
1
New cards
10
\-ve balance factor = right-heavy tree = rotate ?
left
New cards
11
\+ve balance factor = ? = rotate right
left heavy tree
New cards
12
AVL trees have what guaranteed time for all operations
o(logn)
New cards
13
For N nodes =
N-1 edges (parent child relation)
New cards
14
all nodes are accessible through?
root
New cards
15
There is only one path to reach any node from?
root
New cards
16
Trees are a special form of
graphs
New cards
17
Edges can connect any vertex in any possible way
any possible way
New cards
18
Any vertex can be accessed through
any path
New cards
19
A graph is a way of representing relationships that exist between
pairs of objects
New cards
20
A Graph G can be represented as an ordered pair of a set V of vertices and a set E of ?
edges
New cards
21
Edges in graphs can be directed or
undirected
New cards
22
Adjacent Vertices: Two vertices, u and v, connected together via the same ?
edge
New cards
23
An edge is said to be ? to a vertex if the vertex is one of the edge’s endpoint
incident
New cards
24
A ? is a sequence of alternating vertices and edges that starts at a vertex and ends at a ? such that each edge is incident to its predecessor and ? vertex.
path, vertex, successor
New cards
25
Cycle is a path that starts and ends at the same
vertex and includes at least one edge
New cards
26
Undirected Graphs: Edges do not have a ?
direction
New cards
27
Undirected Graphs: Edge (u, v) will be equivalent to the edge ?
(v, u)
New cards
28
Directed Graphs or Digraphs: Edges have a direction pointing from
one vertex to another vertex
New cards
29
Mixed Graphs: Edges have a direction pointing from one vertex to another vertex and some edges are undirected
one vertex to another vertex
New cards
30
Directed Acyclic Graphs: Finite directed graph with no
cycles
New cards
31
Complete Graphs: All vertices are connected to
each other
New cards
32
Unweighted graphs: all edges are of equal weight of
1
New cards
33
Weighted graphs: have different values associated to ?
edges
New cards
34
What is the order that Breadth-First Search (BFS) goes by to visit nodes/vertices
starts from top of height all the way to leafs by row
New cards
35
What is the order that Depth-First Search (DFS) goes by to visit nodes/vertices
starts from left side all the way down to leaf then middle, then right side down to leaf
New cards
36
Time complexity of Breadth-First Search (BFS) ?
O(V+E)
New cards
37
BFS Memory complexity is not good bc it stores many references so ? is usually preferred
DFS
New cards
38
DFS constructs a ? for unweighted graphs (smaller number of edges)
\
Shortest path
New cards
39
DFS uses ?
stack LIFO
New cards
40
BFS uses ?
queue FIFO
New cards
41
Vertex is a
node
New cards
42
edge
lines that connect nodes
New cards
43
time complexity for DFS
o(v+e)
New cards
44
DFS is used to solve
mazes
New cards
45
BFS Walk through all nodes on the same ?
level
New cards
46
BFS is based on
queues
New cards
47
BFS is suitable for searching nearby
vertices
New cards
48
BFS has no concept of
backtracking
New cards
49
DFS goes as deep as possible until there is ?
no neighbor left
New cards
50
DFS is based on
stacks
New cards
51
Suitable for searching vertices farther away from
the source
New cards
52
DFS can recursively ?
backtrack
New cards
53
On what side is the predeccor?
left
New cards
54
on what side is the successor ?
right
New cards
55
if you delete a root node what will be the new root? Predecessor or Successor?
predecessor, largest item in right subtree
New cards
56
Pre-order traversal Visit root node first, then
left-subtree and finally right-subtree
New cards
57
Post-order traversal Visit left-subtree first, then
right-subtree, and finally the root node
New cards
58
In-order traversal Visit left-subtree first, then
root node, and finally right-subtree
New cards
59
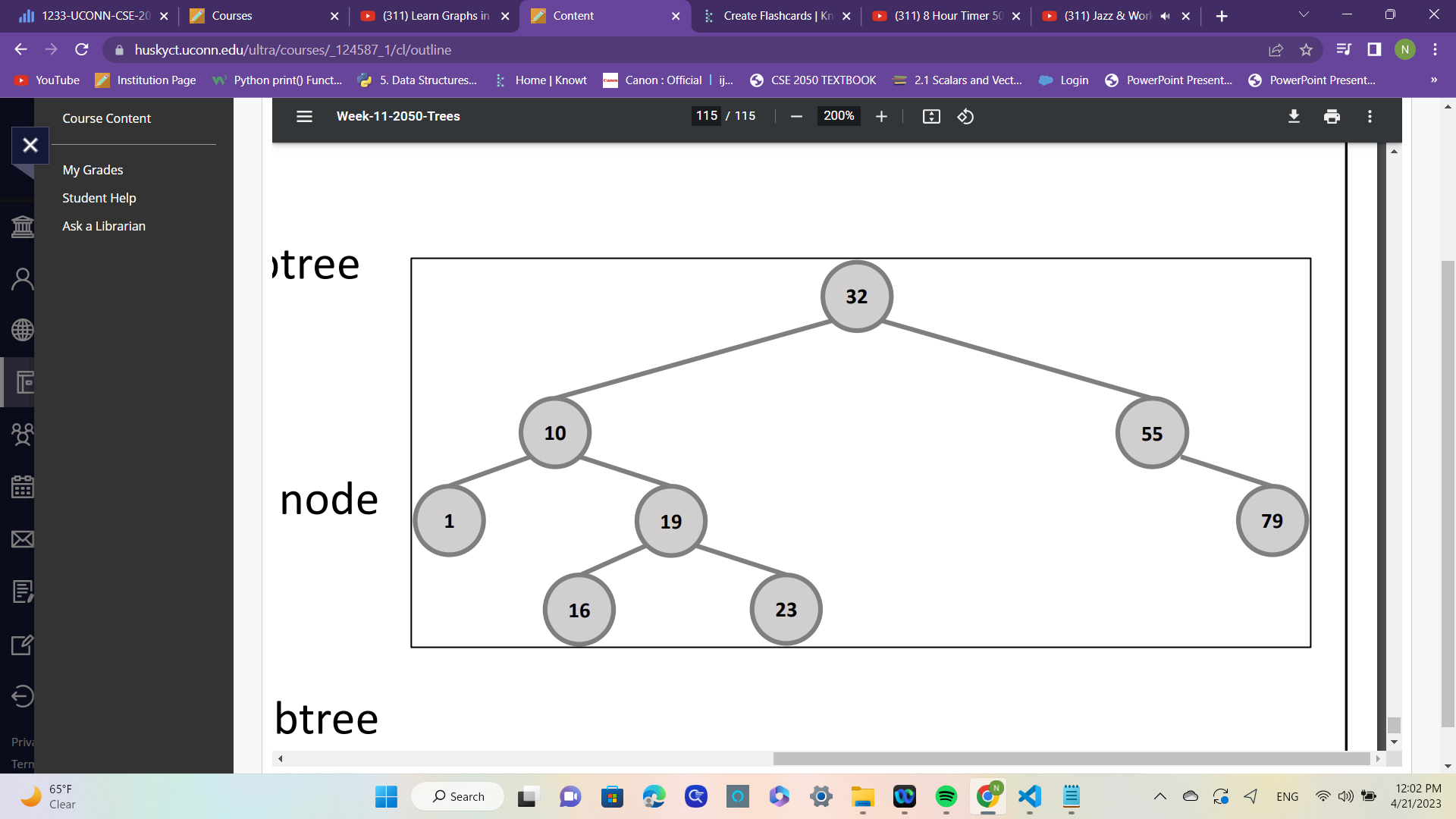
what is the pre order traversal
32,10,1,19,16,23,55,79
New cards
60
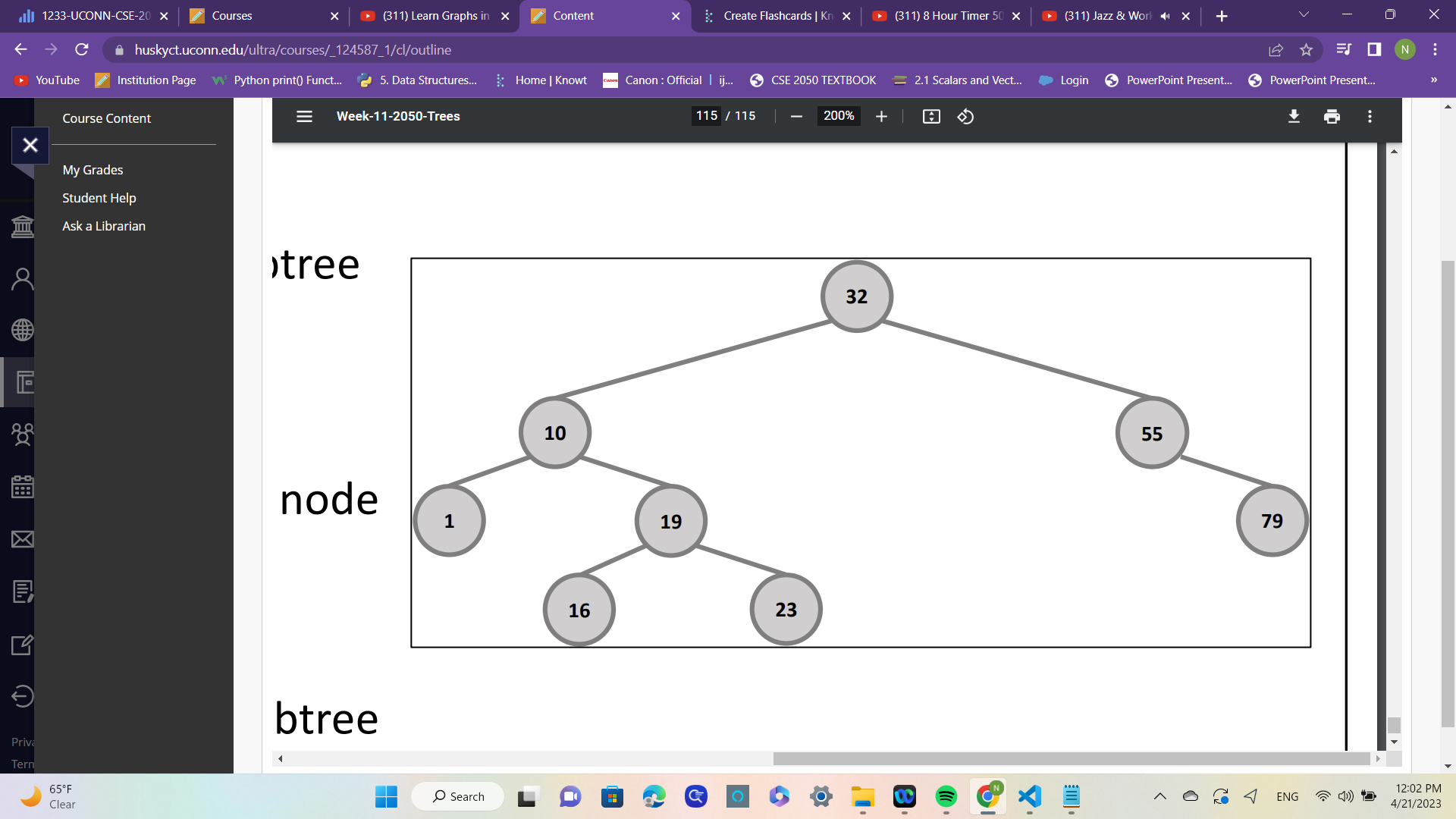
what is the post order traversal
1,16,23,19,10,79,55,32
New cards
61
what is the in order traversal
1,10,16,19,23,32,55,79
New cards
62
stack all operation time
o(1)
New cards
63
queue: dequeue operation time
o(n)
New cards
64
linked list operation time to remove tail element
o(n)
New cards
65
doubly linked list time operation
o(1)
New cards
66
hash tables time operation to locate bucket
o(1)
New cards
67
hash tables time operation to locate element
o(n)
New cards
68
Each element in a tree has a parent element and children
zero/more
New cards
69
Edge: Connection between ? nodes to show a relationship between them
2
New cards
70
Path: A path is an ordered list of nodes that are connected by ?(from top to bottom)
edges
New cards
71
Height of a node x: number of edges in **longest** path from the **node** x to a ?
leaf
New cards
72
Depth/Level of node x: **Number** of **edges** in path from ? to **node** x
root
New cards
73
Degree of a **node**: The number of its ?
children
New cards
74
Degree of a **tree**: Total number of ? in it
nodes
New cards
75
In a tree, there must only be a ? path from the root node to any other node
single
New cards
76
Every node in the tree can have at most ? children (left child and right child)
2
New cards
77
balanced BST time
o(logn)
New cards
78
imbalanced BST time
o(n)
New cards
79
mapping can be defined as an association between
2 objects
New cards
80
mapping associated objects can be referred as
key value pairs
New cards
81
array of key-value pairs are sometimes referred as
associative arrays or maps
New cards
82
Unlike a standard array, indices for a map need not be
consecutive nor even numeric.
New cards
83
Unlike Python, many other programming languages ? have a built-in mapping data type like dictionary
do not
New cards
84
Elements are stored as ? in the list
objects
New cards
85
Searching a particular key requires ? time complexity
o(n)
New cards
86
How does the dictionary have o(1) time complexity for all operations? Python Dictionary is implemented with another?
data structure
New cards
87
• We can pass any “?”of key into a mechanism to convert it into indices/codes
type
New cards
88
The goal of a hash function, h, is to map each key, k, to an integer in the range \[?\]
\[0, N - 1\]
New cards
89
N in \[0, N - 1\] is the ?
capacity of a hash table
New cards
90
what is the value of “Tim” in the map, M, containing N=11 memory locations?
1
New cards
91
Ali = ? % 11
3
New cards
92
Sue = ? % 11
4
New cards
93
Mia = ? % 11
4
New cards
94
if N=11 memory locations what is the last value of the index
10
New cards
95
We can store multiple items in any
specific bucket
New cards
96
what is a bucket in code
M\[j\]
New cards
97
M is the ? of buckets
array
New cards
98
j is the
index generated by hash function
New cards
99
Time to search for the bucket is
O(1)
New cards
100
Time to search a key in the bucket depends on the size of the bucket. So for size m time complexity is
Studied by 2 people
Note 
Flashcard (37)