les matrices

C’est quoi A^{t} pour A ?

C’est sa matrice transposée

C’est à dire que lignes et colonnes ont été échangées

Comment additionner deux matrices ?

Il faut deux matrices de la même forme (taille) et on additionne entre eux les coefficients à la même place

Comment on multiplie une matrice par un nombre ?

On multiplie tous les coefficients de la matrice par ce nombre

Comment multiplie t on deux matrices ?

La matrice de gauche doit avoir le même nombre de colonne que le nombre de ligne de la matrice de droite

1. Tourner la matrice de gauche de 90º vers la droite (on la met debout)

2. Faire passer la colonne la plus à droite (anciennement ligne la plus haute) dans la matrice de droite

3. Quand cette « colonne » arrive sur la première colonne de la matrice de droite : additionner entre eux les produits de tous les facteurs des coefficients à la même place

4. C’est le coefficient 1,1 de la matrice résultat

5. Faire passer la « colonne » dans la colonne suivante de la matrice de droite et répéter l’addition de produits

6. C’est le coefficient 1,2

7. Répéter jusqu’à ce que la « colonne » ait fini la traversée de la matrice de droite, à ce moment là changer de ligne sur la matrice résultat et passer à la « colonne » de la matrice de gauche suivante

Comment s’écrit le format d’une matrice ?

Matrice m x n (se lit m par n)

Matrice à m lignes et n colonnes

Comment désigner un coefficient au sein d’une matrice ?

a_{ij} Est un coefficient de la matrice A situé à la ligne i colonne j

C’est quoi une matrice carrée d’ordre n ?

Une matrice de taille n x n

Comment appelle t on une matrice de taille 1 x m ?

Une matrice ligne d’ordre/de taille m

Comment appelle t on une matrice de taille n x 1 ?

Une matrice colonne d’ordre/de taille n

C’est quoi une matrice identité de taille n ?

Notée I_{n} → matrice carrée d’ordre n dont tous les éléments diagonaux valent 1 et tous les autres valent 0

C’est quoi une matrice nulle de taille m x n ?

Notée 0_{m,n}

Matrice de taille m x n dont tous les éléments valent 0

Quel type de matrice forme les coordonnées d’un point ?

Matrice ligne

Quel type de matrice forme les coordonnées d’un vecteur ?

Matrice colonne

C’est quoi une matrice symétrique ?

Les éléments a_{ij} sont égaux aux élémentsa_{ji}

La somme de matrice fonctionne exactement comme ?

Les sommes normales

• commutatives

• Associatives

Quelle est la propriété d’un produit nombre par matrice ?

Ce produit est distributif

Qu’est-ce qu’une matrice opposée ?

L’opposé de la matrice A de taille m x n est la matrice M vérifiant A + M = M + A = 0_{m,n}

Notée -A

Le produit de matrice est il distributif ?

Oui si l’ordre des facteurs est conservé :

A x (B+C) = A x B + A x C ≠ B x A + C x A

Le produit de matrices est il associatif ?

Oui toujours si l’ordre est conservé

Ça veut dire quoi associatif ?

(a + b) + c = a + (b + c)

Ou alors

(a*b)*c = a*(b*c)

Ça veut dire quoi que la matrice identité est un facteur neutre ?

Multiplier une matrice par la matrice identité revient à multiplier un nombre par 1 : le résultat est inchangé

Quelle matrice est le terme neutre de l’addition ?

La matrice nulle

A * 0_{mn} = ?

0_{mn}

Quelle est la condition nécessaire pour qu’il existe une matrice A^n ?

La matrice A doit être carrée

Que vaut A^1 ?

A

2^1 = ?

2

6^0 = ?

1

1 est le facteur neutre

A^0 = ?

I_{n}

I_{n} est le facteur nul

Qu’est-ce que A^{-1} ?

C’est la matrice inverse de A

Donc\frac{I_{n}}{A}

Donc la matrice pour laquelle A * A^{-1} = I_{n}

Toutes les matrices carrées sont elles inversibles ?

Non

Si B est l’inverse de A, comment puis je appeler B ?

A^{-1}

Quand une matrice carrée d’ordre 2, nommée A, est elle inversible ?

Si det(A) ≠ 0

Qu’est ce que det(A)

C’est le déterminant de A

det(A) = (\sum produits des coeff des diagonales vers la droite) - (\sum produits des coeff des diagonales vers la gauche)

Trouver simplement A^{-1} si A est une matrice carrée d’ordre 2 ?

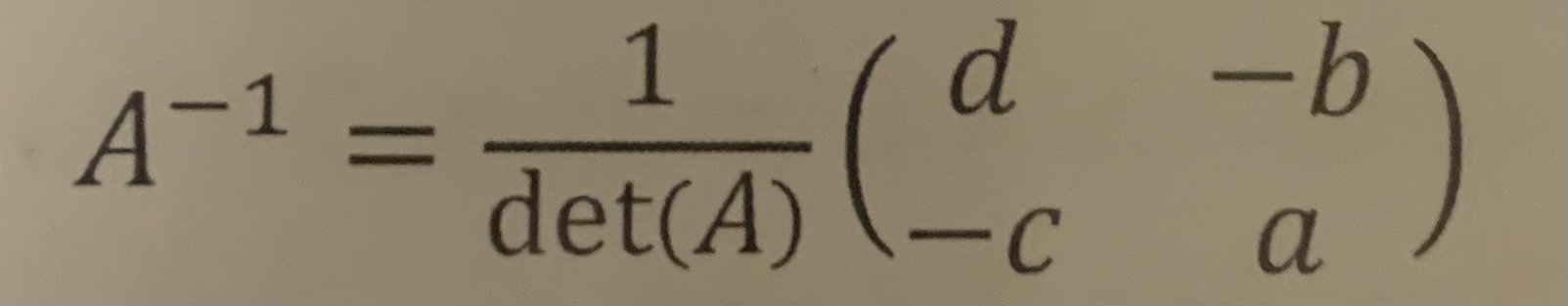
Règle de Cramer

Si A est une matrice carrée inversible d’ordre n alors le système linéaire A * X = B admet une unique solution : X = A^{-1} * B

Démontrer que pour A*X = B

X = A^{-1} * B

A*X = B

A^{-1} \cdot A\cdot X = A^{-1} \cdot B

I_{n} \cdot X = A^{-1} \cdot B

X = A^{-1} \cdot B

\frac{\frac54}{\frac23} = ?

\frac54\cdot\frac23

Résoudre un système d’équations avec des matrices ?

1. On écrit toutes les équations afin que dans chaque les inconnues soient dans le même ordre

2. On crée 3 matrices :

La matrice A → les coefficients dans le même ordre (ligne colonne tout pareil)

La matrice X → les inconnues dans l’ordre de haut en bas

La matrice B → les solutions dans l’ordre (pareil que dans le système c’est en colonne)

3. On fait une équation de matrices : si la matrice A n’est pas inversible le système a soit aucune soit une infinité de solutions