13.1 - Oscillations

What are the two conditions required for an object to oscillate with SHM?

1. The restoring force is directly proportional to the displacement.

2. The restoring force always acts towards the equilibrium position.

What is angular frequency?

Angular frequency is a measure of the rate of rotation of an object.

Give two equations for angular frequency.

ω = 2π/2

ω = 2πf

What are two types of oscillations that an object can experience?

1. Free oscillations

2. Forced oscillations

What is the frequency of a freely oscillating object equal to?

Freely oscillating objects will vibrate at their natural frequency.

What is resonance?

Resonance is where the amplitude of oscillations of an object drastically increase due to gaining an increased amount of energy from the driving force.

This occurs when the driving frequency equals the natural frequency of the object.

What can be said about an object undergoing resonance?

The object will be oscillating at its maximum amplitude and the rate of energy transfer is at a maximum

What is damping?

Damping occurs when energy energy is lost from and oscillating system due to an external force acting on it.

What are the three types of damping?

1. Light Damping

2. Critical Damping

3. Heavy Damping

What is critical damping?

Critical damping is when the damping causes the object to return to the equilibrium position in the quickest time possible without oscillating.

State the equation for the total energy stored in a simple harmonic oscillator.

Energy stored = ½ kA²

where k is the spring constant, and A is the amplitude.

If the following graph shows displacement against time, what would the velocity-time graph and acceleration-time graphs look like?

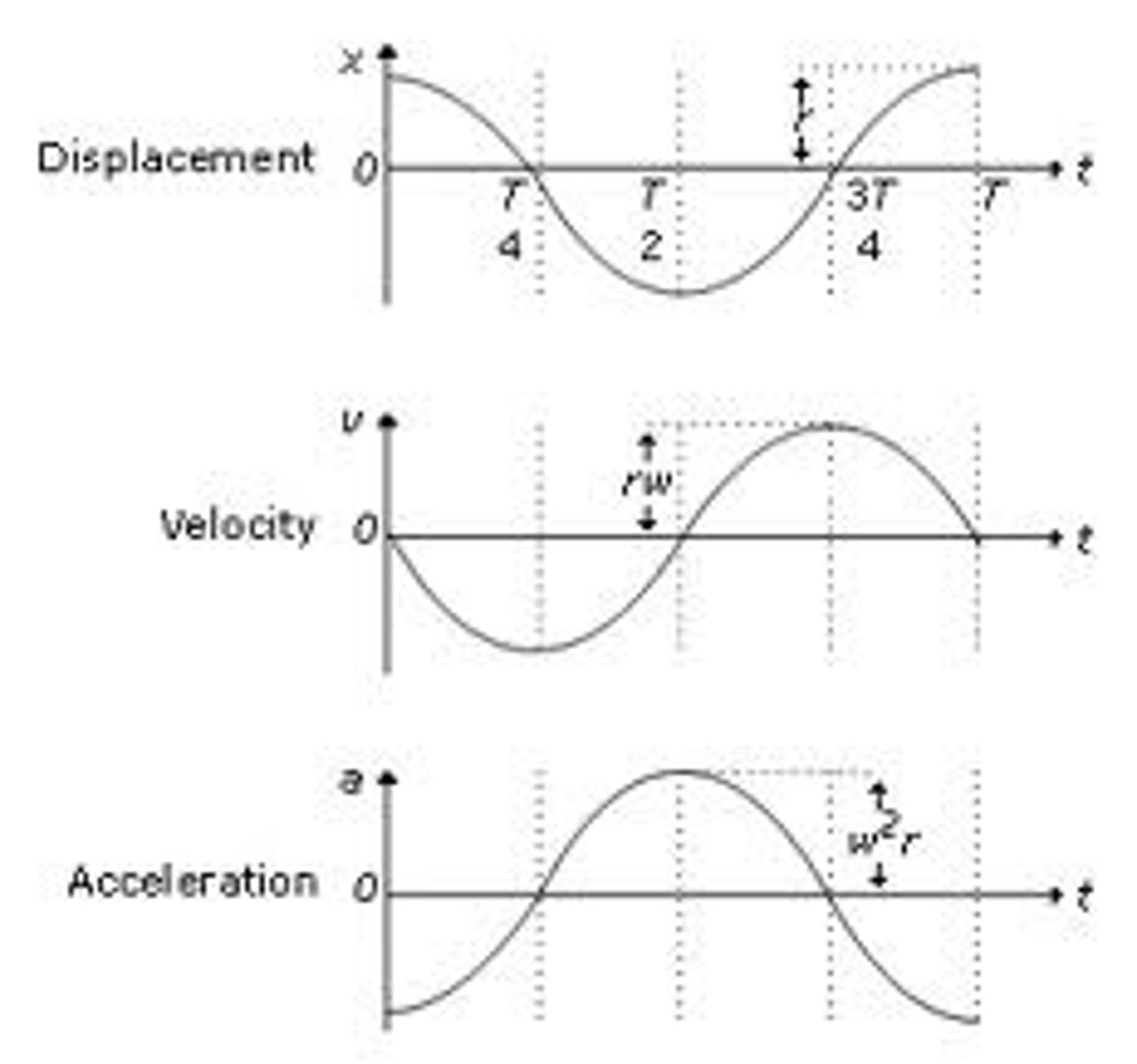
What is the difference between free and forced oscillations?

When an object oscillates without any external forces being applied, it oscillates at its natural frequency. This is known as free oscillation. Forced oscillation occurs when a periodic driving force is applied to an object, which causes it to oscillate at a particular frequency.

How can time period be calculated for a mass-spring system and a pendulum respectively?

T = 2π√m/k

For a mass-spring system where m is mass/kg and k is the spring constant/Nm⁻¹

T = 2π√l/g

For a pendulum where l is the string length/m and g is the gravitational field strength /ms⁻²