PH2. Analyzing and Describing Motion

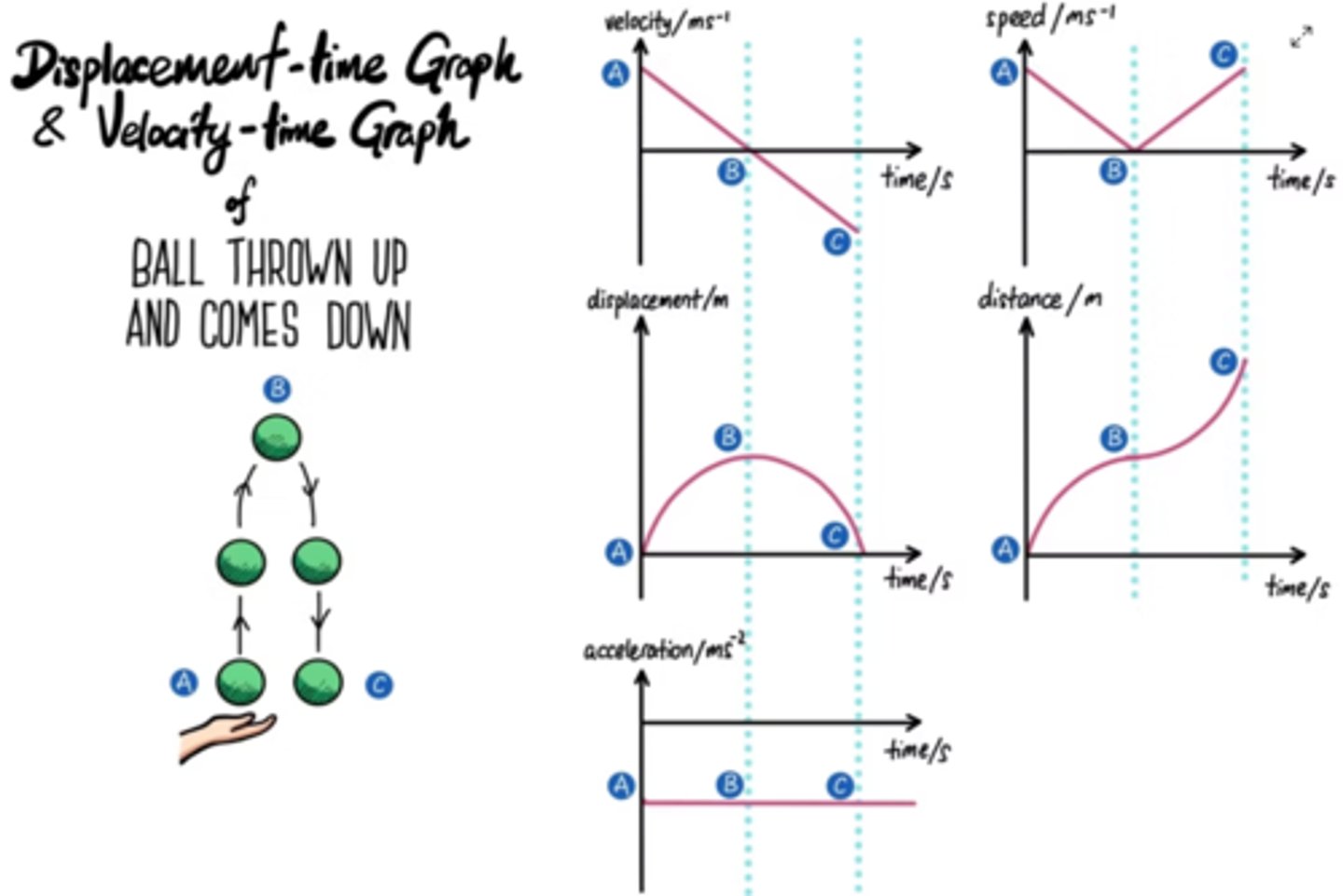
What are the graphs for a ball which is thrown, falls, and is caught

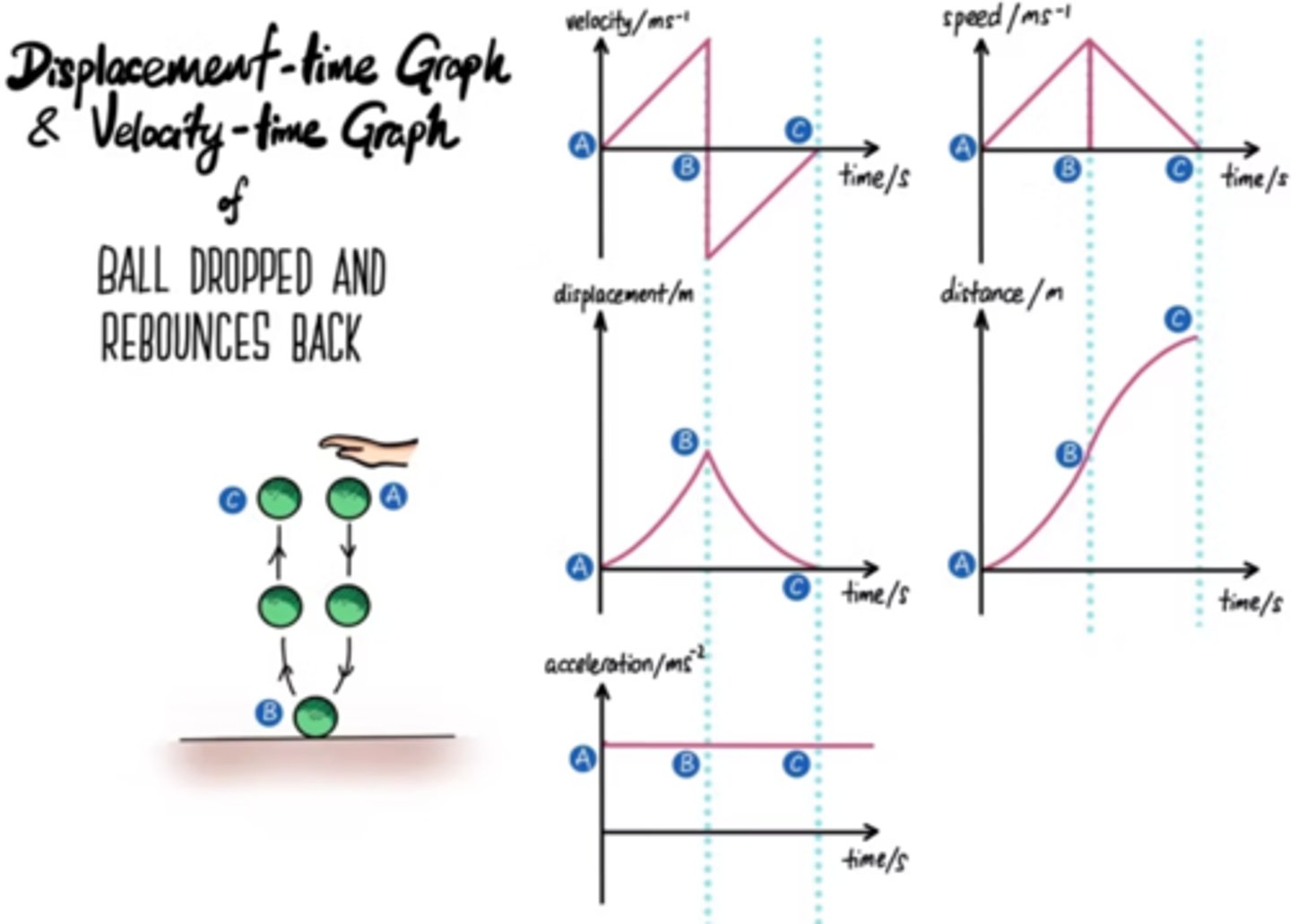
What is the difference between the graphs for a ball which falls, bounces and is caught?

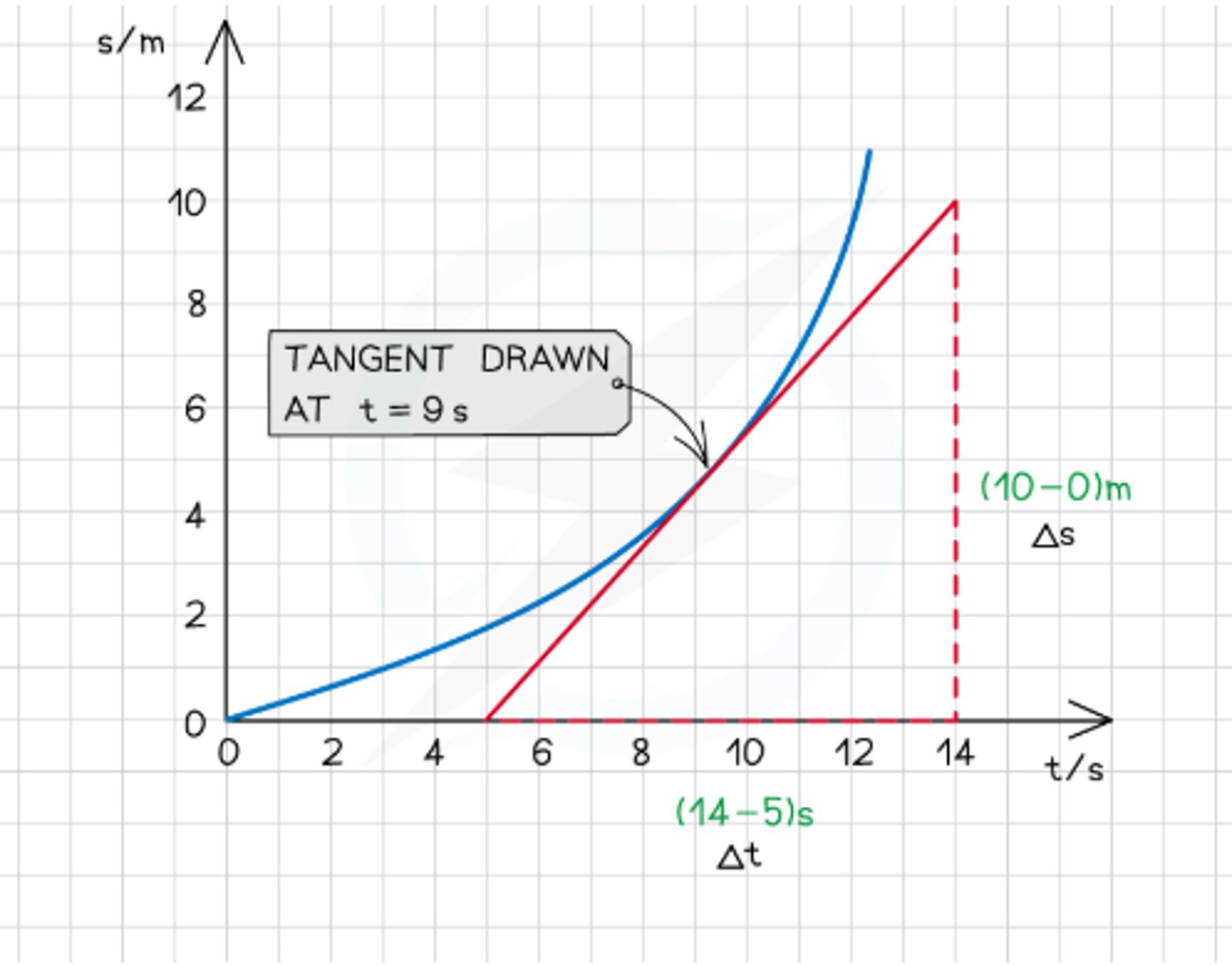
How do you find the instantaneous velocity on a curved displacement-time graph?

Draw a tangent at the point and calculate its gradient

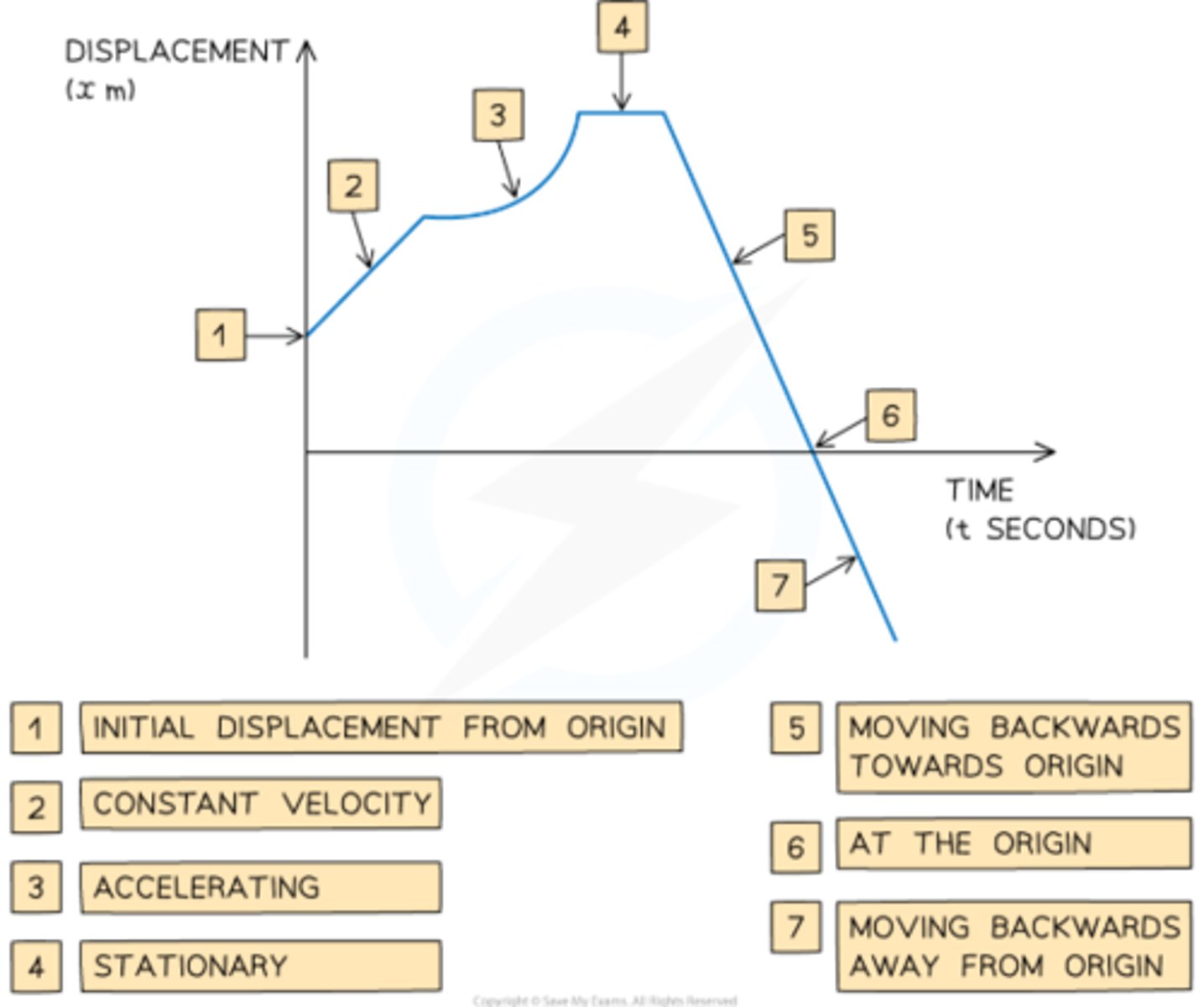
How do you interpret the shape of a displacement-time graph?

- Horizontal line = zero displacement

- Straight line = constant velocity

- Curved line = acceleration

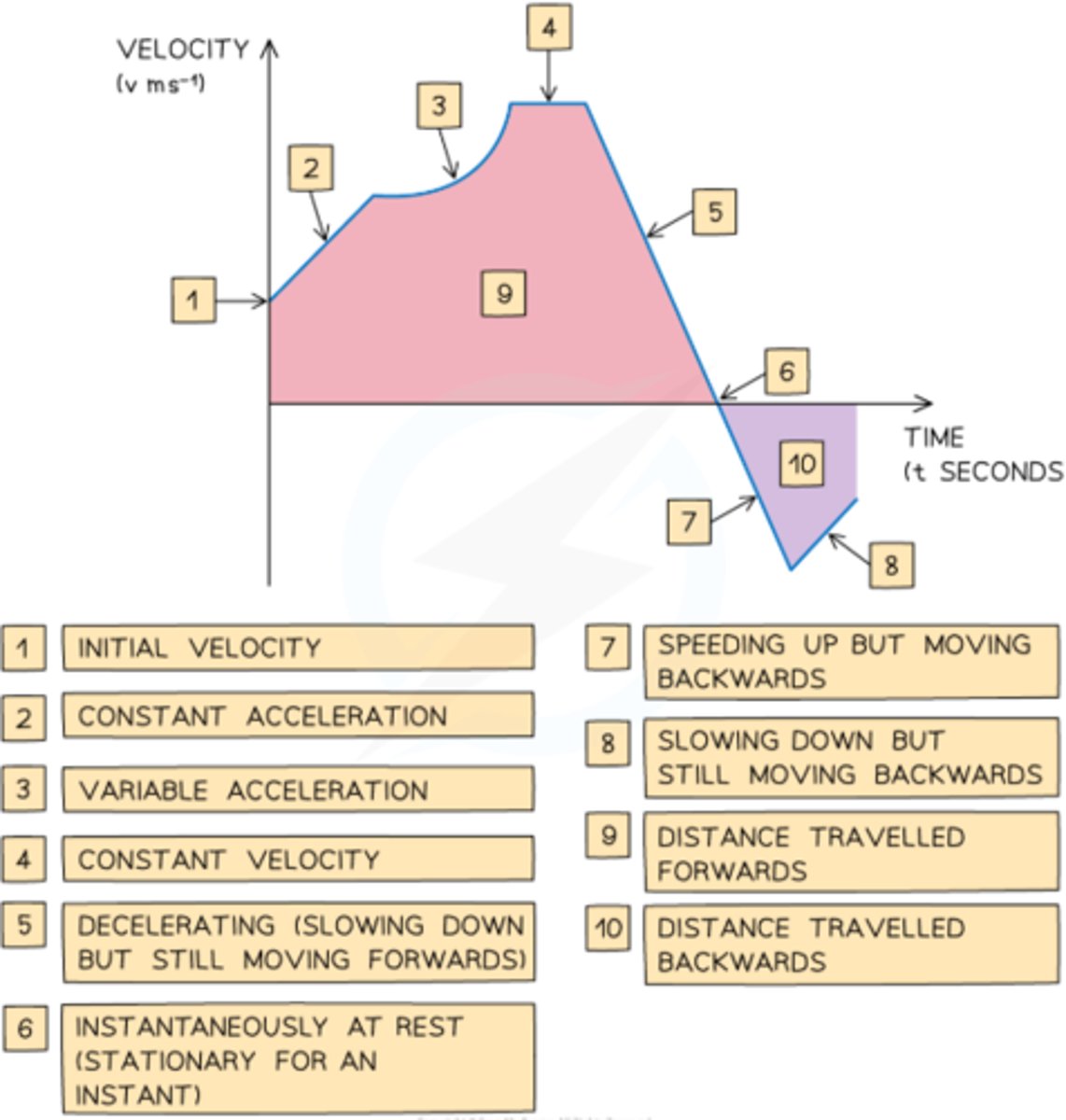
How do you interpret the shape of a velocity-time graph?

- Horizontal line = constant velocity

- Straight line = constant acceleration

- Curved line = changing acceleration

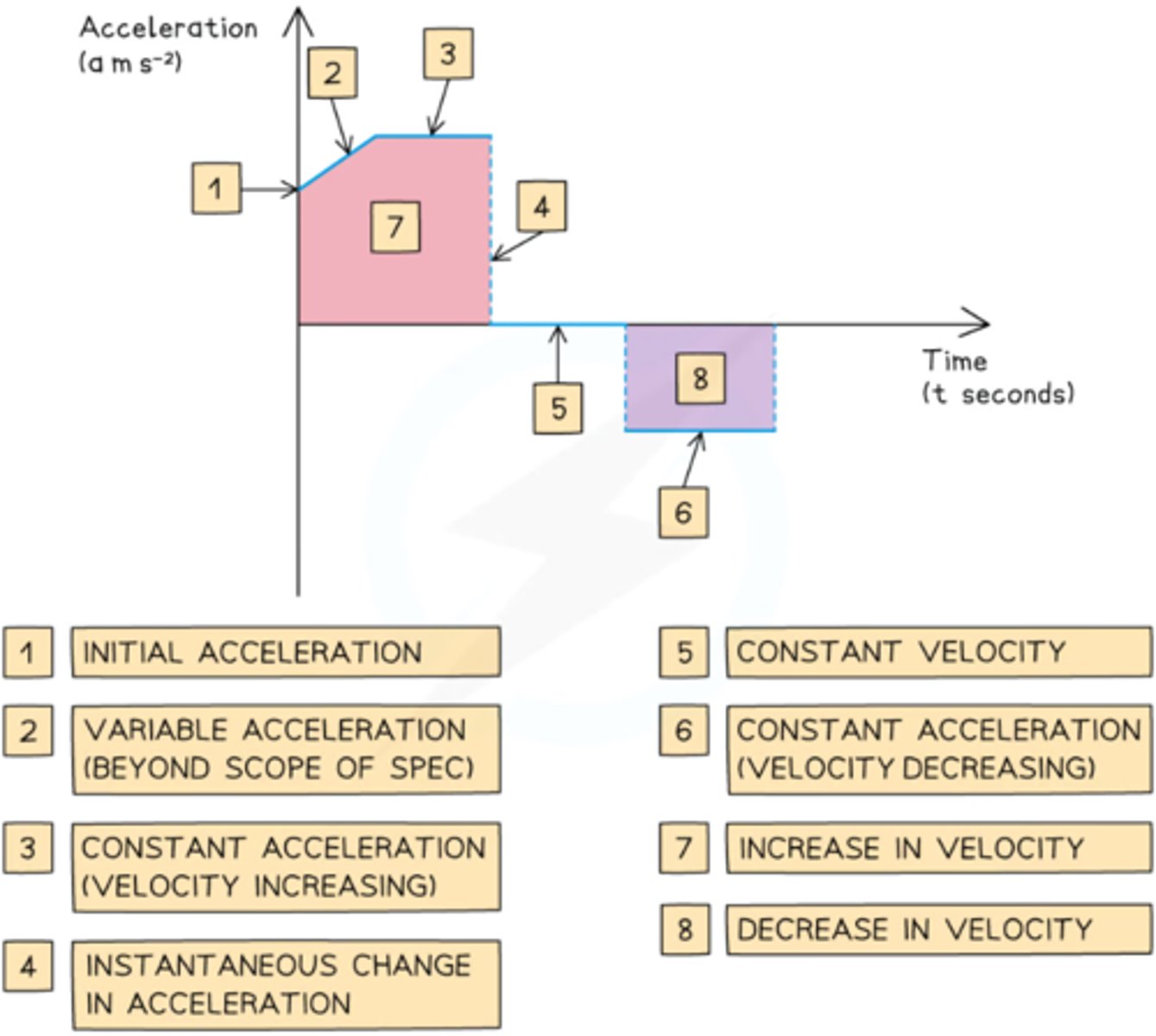
How do you interpret the shape of an acceleration-time graph?

- Horizontal line = constant acceleration

- Straight line = changing acceleration

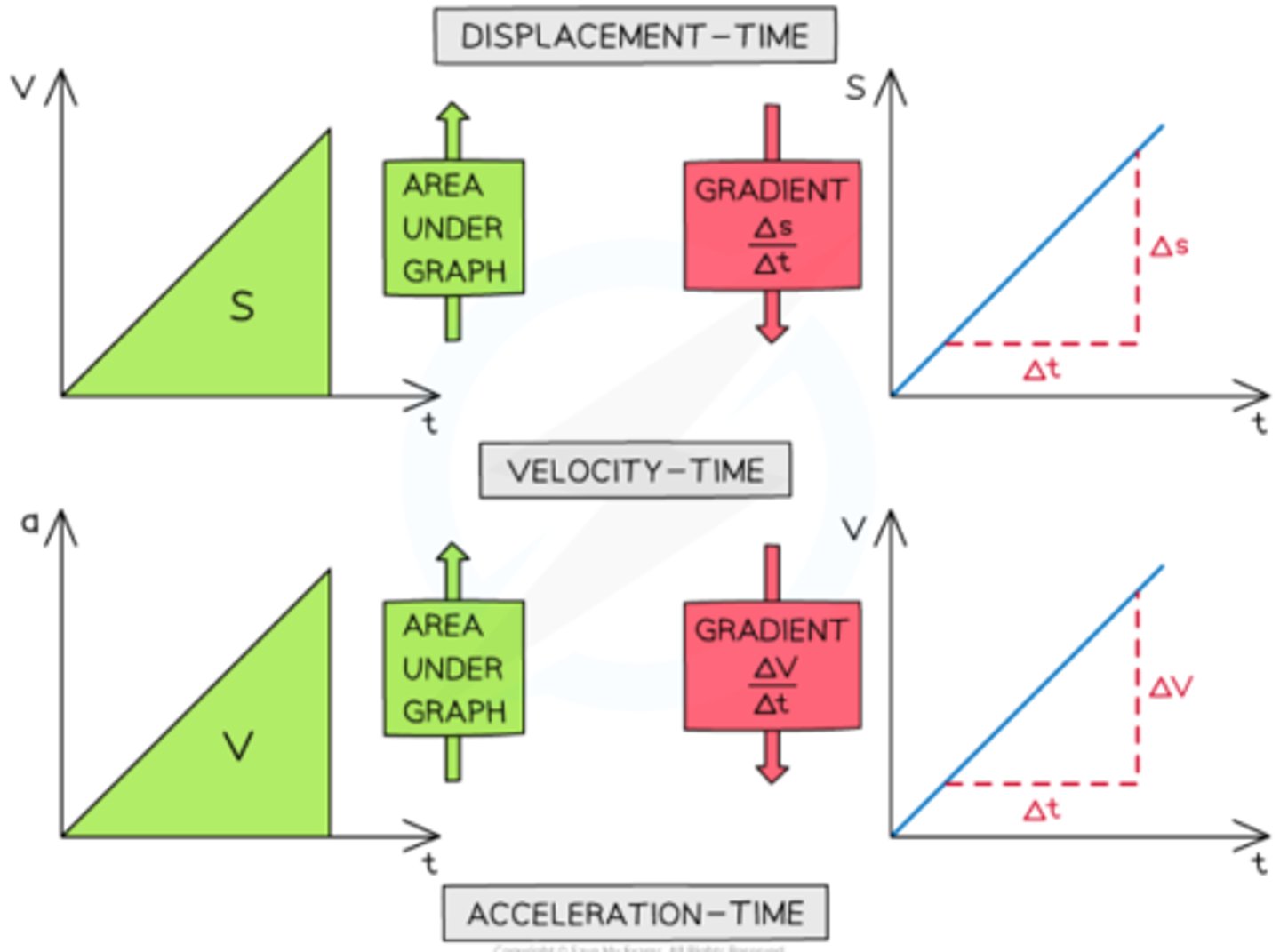
What do the y-intercepts, gradients and areas under graphs represent?

Y-intercept: initial quantity

Gradient of:

- Displacement-time graph is velocity

- Velocity-time graph is acceleration

Area under:

- Velocity-time graph is displacement

- Acceleration-time graph is velocity

What are the key features of a bouncing ball's motion at its highest and lowest points under uniform gravity, ignoring air resistance?

Highest Point (A):

Zero velocity

Maximum displacement

Velocity changes from positive to negative

Lowest Point (B):

Constant velocity if no energy loss

Velocity changes from negative to positive

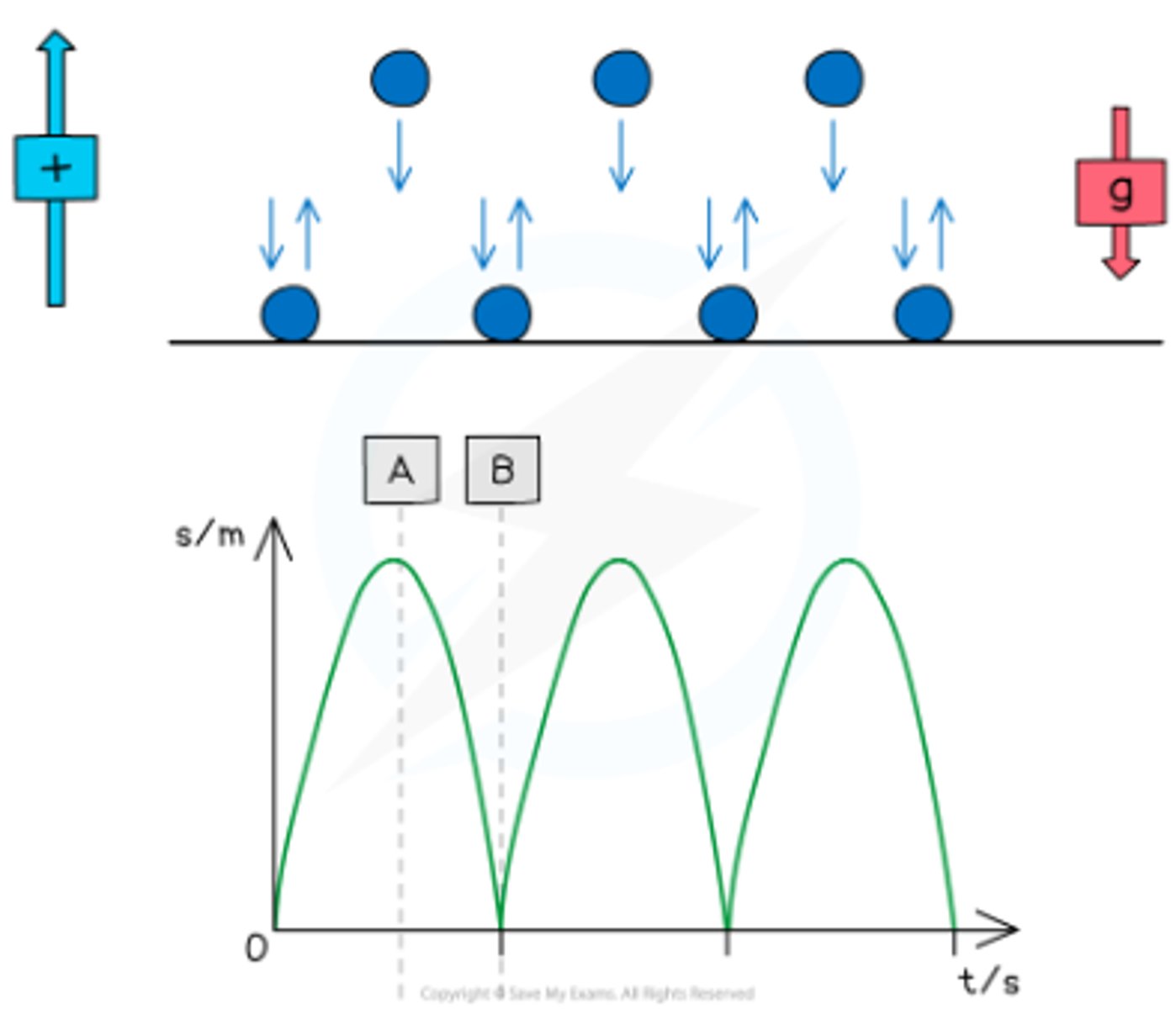
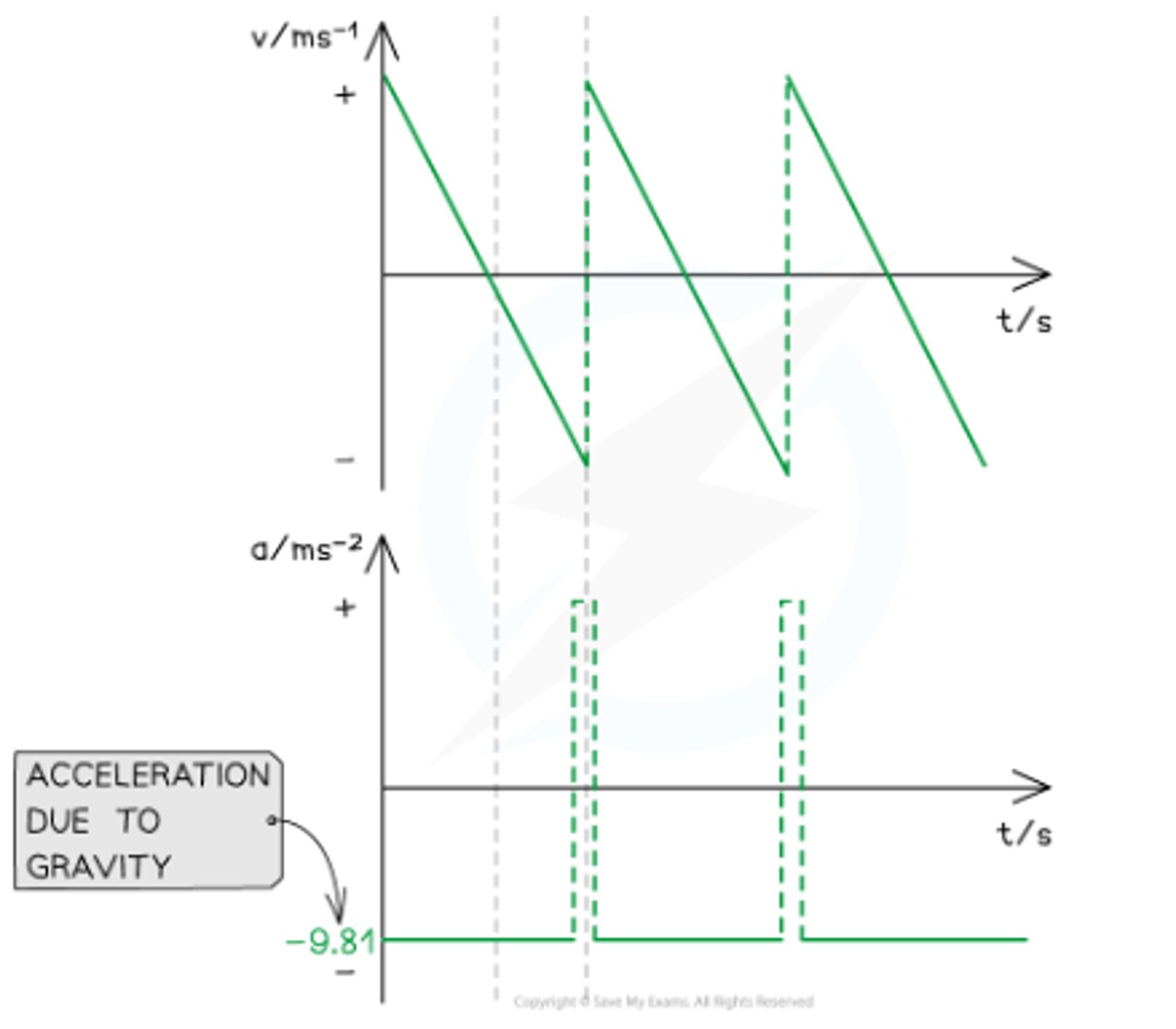
What general principles describe the motion of a bouncing ball under uniform gravity, ignoring air resistance?

- Constant acceleration downwards due to gravity = 9.8 m s-2

- Positive velocity = upward motion, negative velocity = downward motion

- Deceleration during ascent, acceleration during descent

- Same height after each bounce if air resistance is negligible

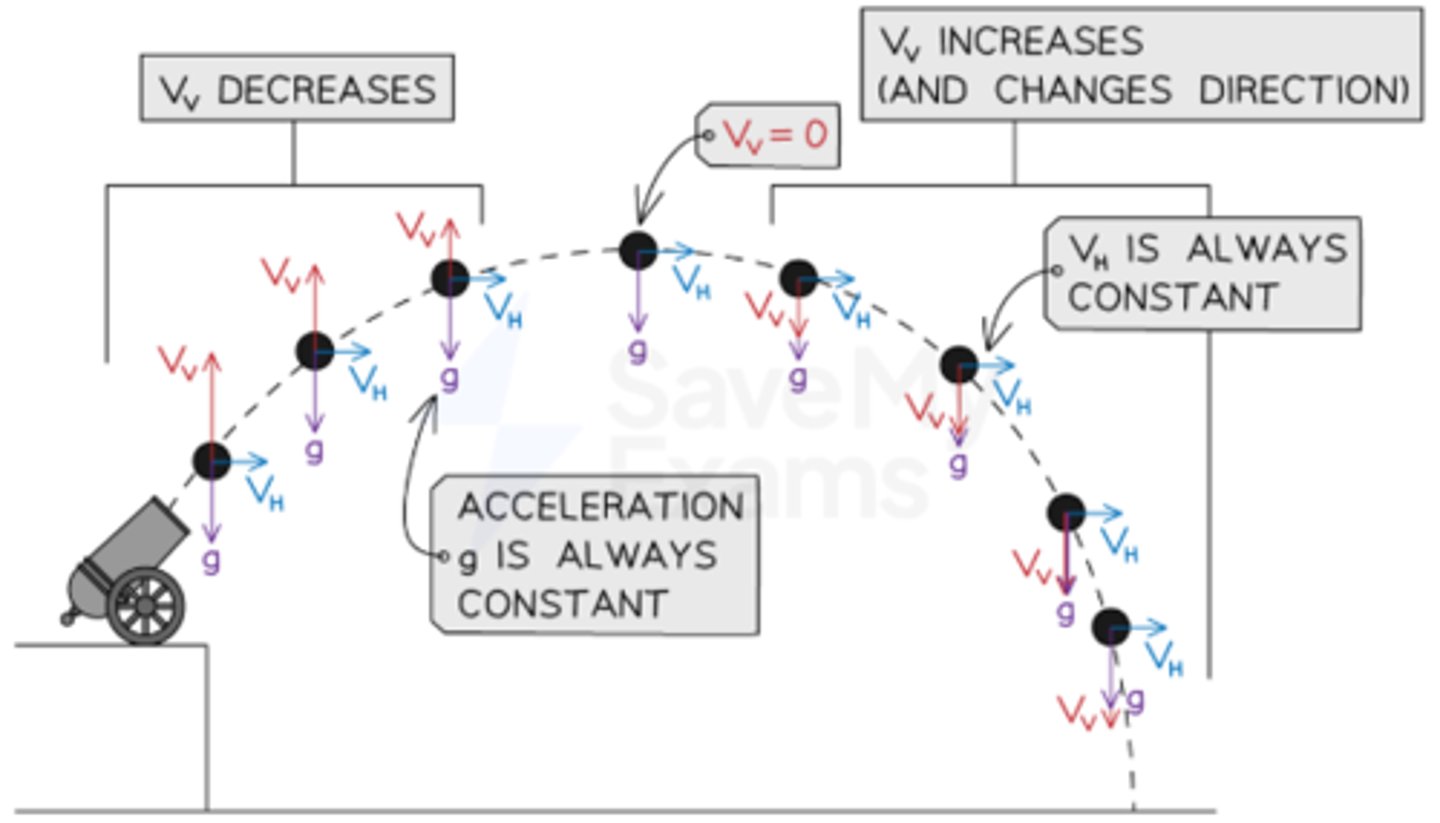
What is a projectile?

Any object that moves through the air, acted on only by gravity, as drag forces are negligible

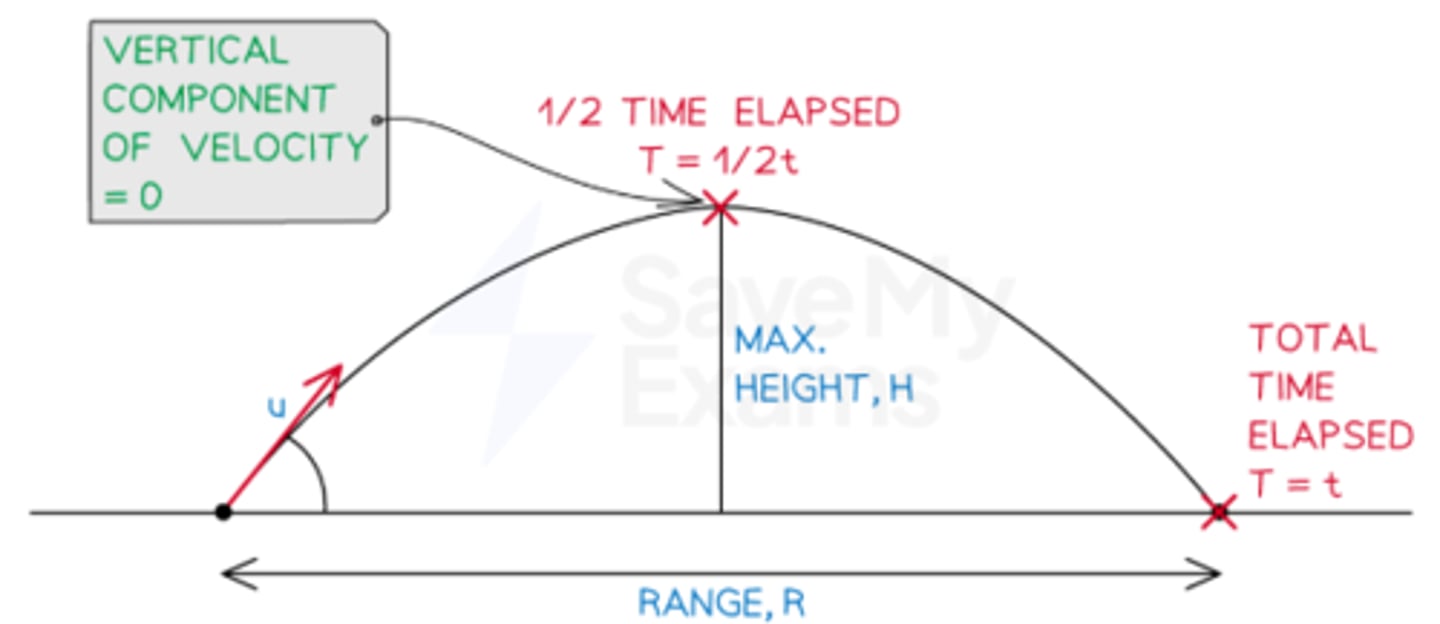
What are the differences between the horizontal and vertical component in projectile motion?

Horizontal Component:

- Displacement is maximum range at end of motion

- Velocity is constant

- Acceleration is zero

Vertical Component:

- Displacement is maximum height at midpoint (half-time)

- Velocity is zero at maximum height

- Acceleration is g = 9.8m s-2 (positive downward, negative upward)

What are the horizontal and vertical components of motion for an object projected horizontally with an initial speed U?

Horizontal Motion:

Displacement x = Ut (constant speed)

Velocity vx​ = U (constant)

Vertical Motion:

Displacement y = ½gt² (accelerated by gravity)

Velocity vy​ = −gt (downward acceleration)

Why do two objects—one dropped vertically and the other projected horizontally—hit the ground simultaneously?

- Time of flight depends on the vertical component of motion

- Time is constant as g is constant and height is same

How can we use SUVAT equations to determine the time of flight?

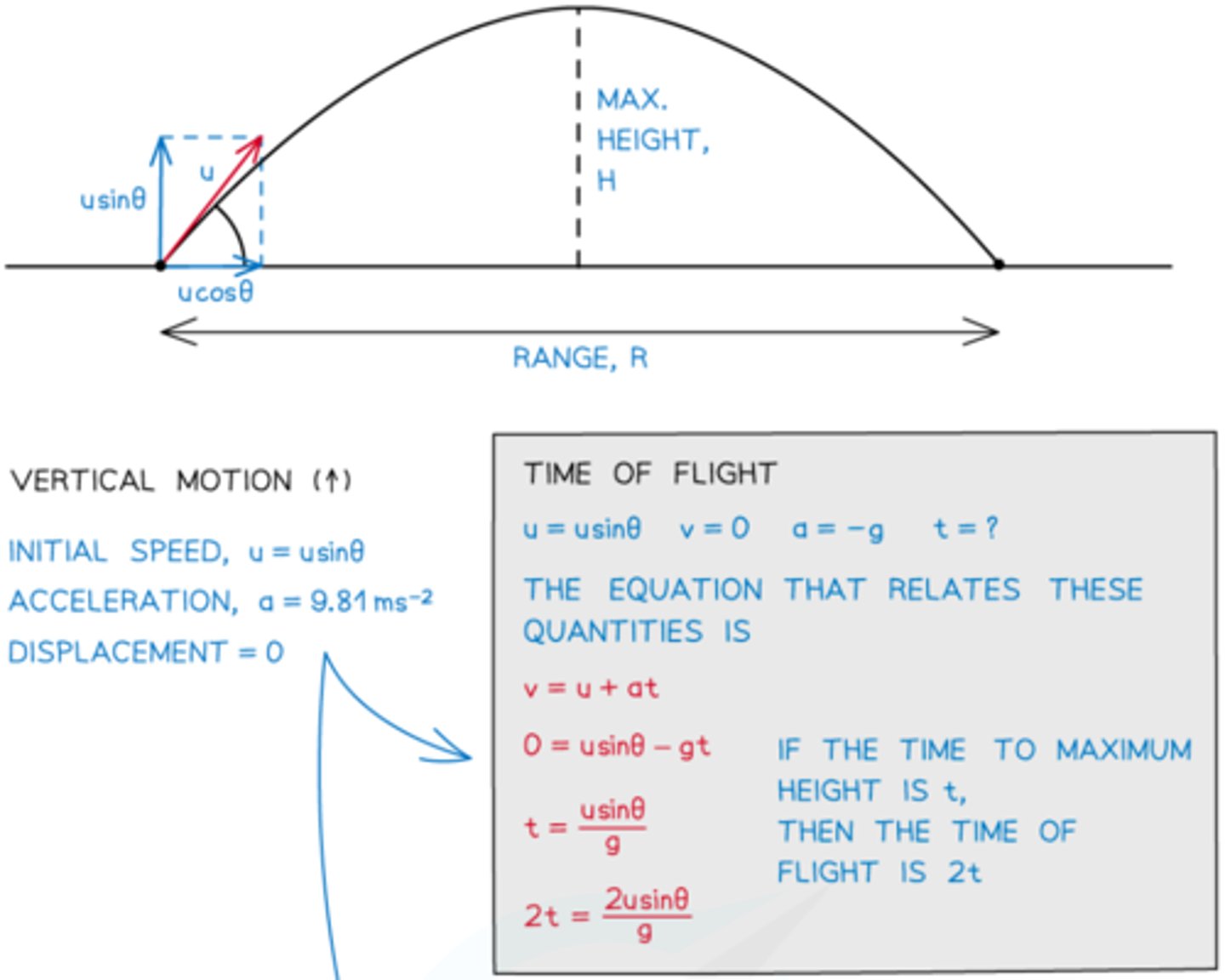
How can we use SUVAT equations to determine the maximum height?

How can we use SUVAT equations to determine the horizontal motion?

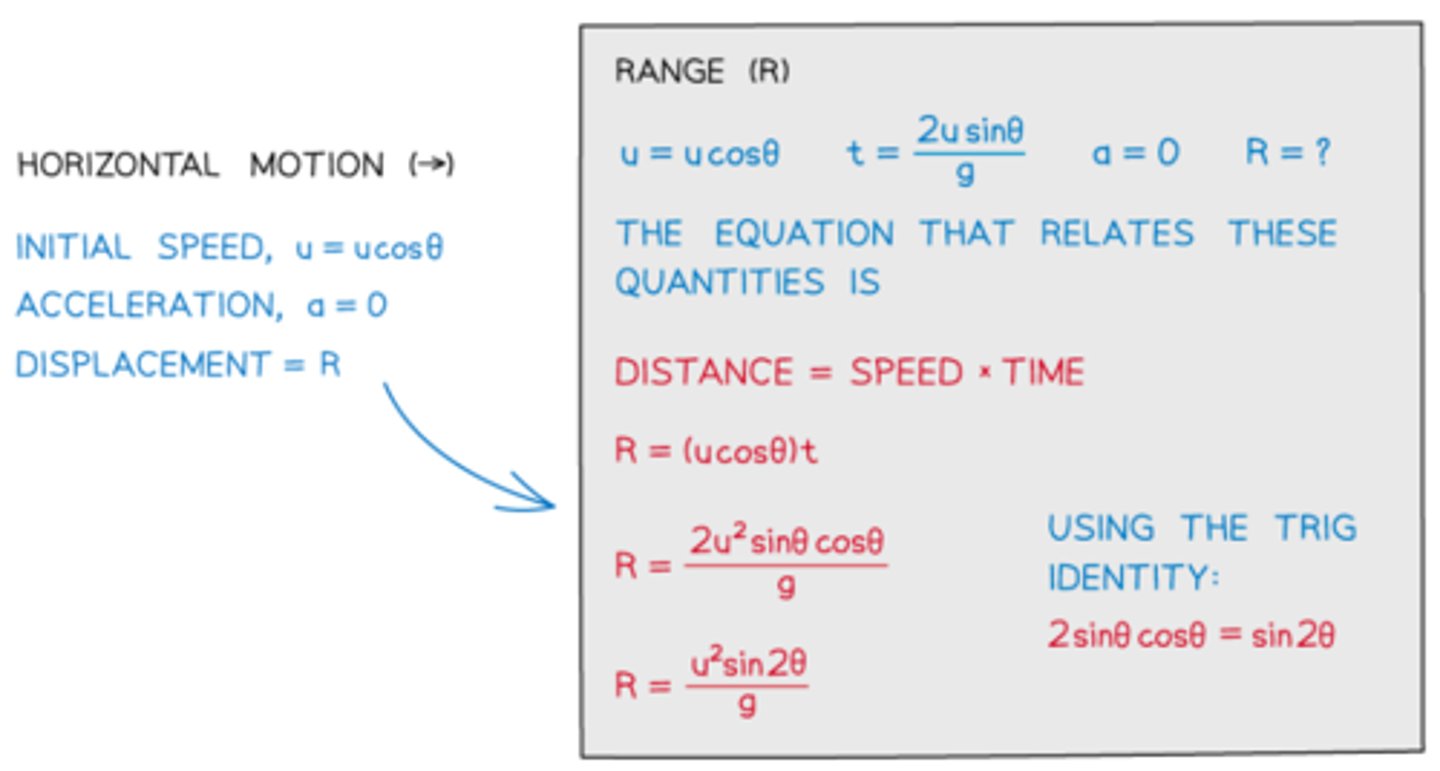
How does air resistance affect maximum height and range of a projectile?

- Slows down both components of velocity

- Work done against air resistance reduces kinetic energy

- So maximum height is reached sooner

- Therefore, vertical and horizontal distance decreases

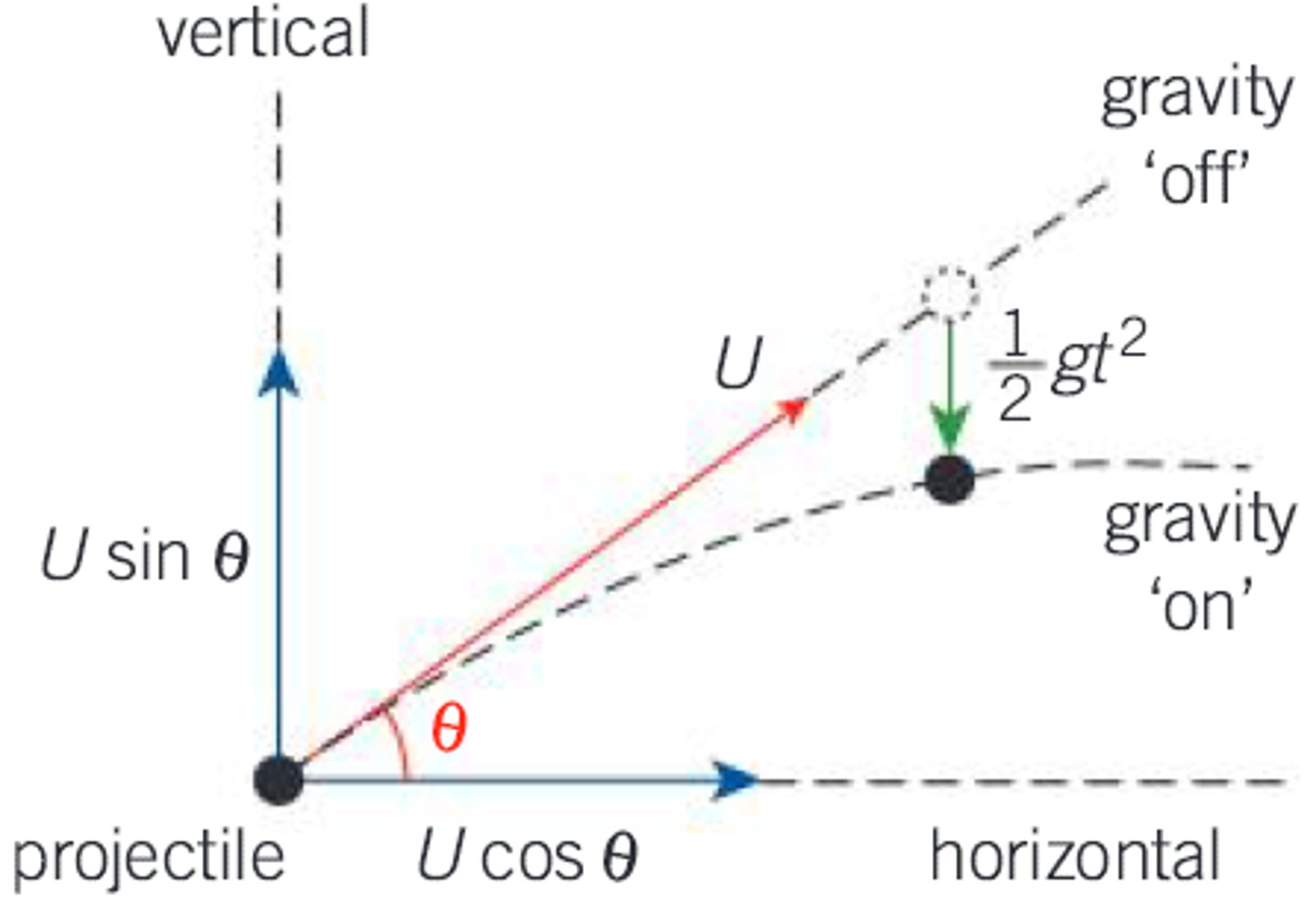
What would the motion of a projectile look like if gravity were switched off and air resistance were negligible?

Without gravity:

- Projectile travels in a straight line at constant velocity due to initial launch force

- Horizontal displacement is constant x=Utcosθ

- Vertical displacement is constant y=Utsinθ

With gravity:

- Vertical velocity decreases by gt due to gravitational acceleration

- Vertical displacement decreases by ½gt², creating a parabolic trajectory