Confidence Interval Week 3/Module 3

Confidence interval

1. 95% interval → means that we are 95% confident that the true population parameter is contained within the confidence interval.

   1. If we repeatedly take random samples and construct intervals from them, about 95% of those intervals would contain the true population parameter does

2. “plausible range where we expect our true population parameter to fall”

---

Writing def

• An interval in which for 95% of samples with intervals created for them have the true mean within the interval

  • And distance between statistic and true mean is < 1.96

Wrong interpretations of CI

• CI represents the probability that the true parameter value is contained within the interval

  • NO!

  • Population parameter has only 1 value, if you repeat the sampling process, the population parameter still has only 1 value

    • it is either in the interval or isn’t in it

Larger Confidence Intervals implications (99vs95)

• 99% means larger intervals

  • because you need larger ranges to make sure you have a better chance to cover the true mean

  • so intervals are wider

Sample size and confidence intervals

• as the sample size increases, the intervals become narrower

SD magnitude and confidence intervals

• Smaller SD means narrower values

Formula for confidence intervals

1. used to find the appropriate standard errors in calculations

   1. qnorm(%+remaining area of left or right)

      1. or 1-CI for a and a/2 for second part

   2. so for 90% it would be (0.9+0.5) = qnorm(0.95)

1. 95% corresponds to 1.98 in a t-dist since the area becomes n-1 = 99

2. t_critical <- qt(0.975, df)

CI depends on the sample you collect

• since the Confidence Interval depends on a given sample

  • if you collect a different sample your CI will almost certainly be different

Point estimate

1. Best estimate of the population parameter value

Confidence vs Precision trade-off

1. Higher level of confidence → larger interval, less precise

Percentile method

• This method sets the lower endpoint of the confidence interval at the 2.5th percentile of the bootstrap distribution and similarly sets the upper endpoint at the 97.5th percentile. The resulting interval captures the middle 95% of the values of the sample mean in the bootstrap distribution.

theory based CI

Quantiles for the CI

Z-score

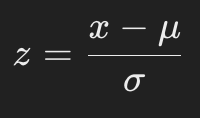
CI for proportion via CLT

• ci_lower <- qnorm(0.025, phat, sqrt(phat*(1-phat)/n))

• ci_upper <- qnorm(0.975, phat, sqrt(phat*(1-phat)/n))

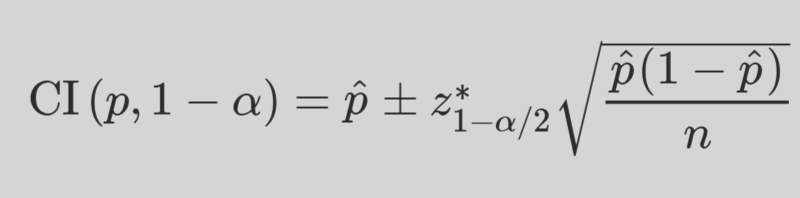
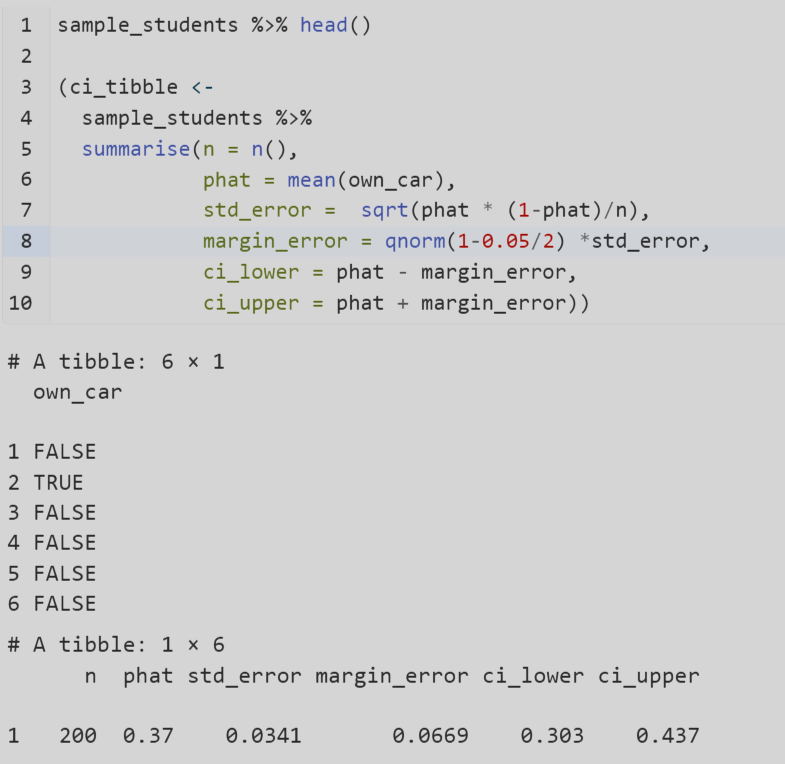
R code for proportion

General formula for CI for a parameter

SE^(0^) is the estimated std. error

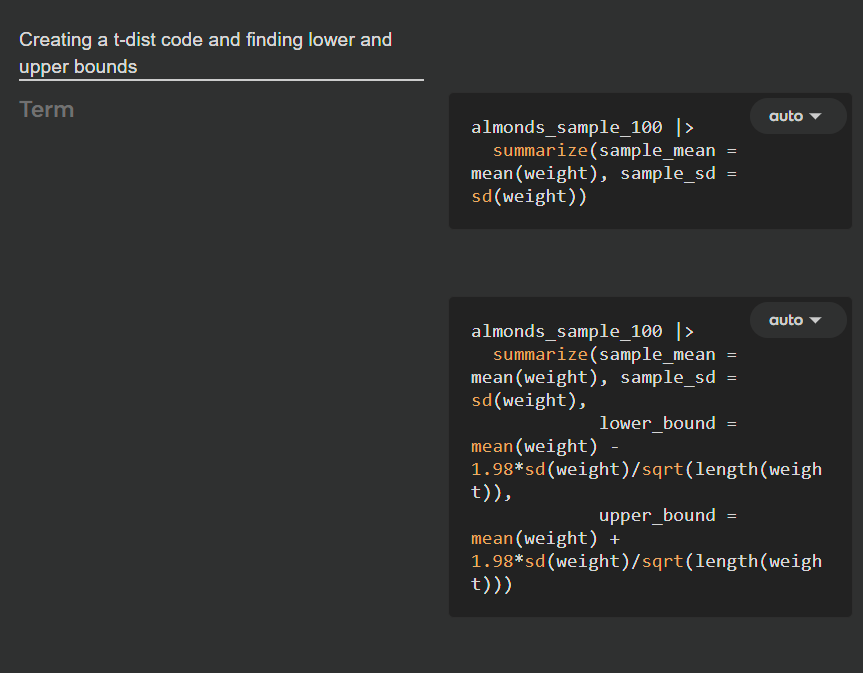
Code for confidence interval for one mean using a t-dist

• when specifying a quantile from a t distribution (t*), you need to specify the degrees of freedom, as well as the quantile you want

• 1−α is the confidence level (e.g., 95% confidence means α=0.05).

• X- is the sample mean, an estimate of mu

• tn−1,1−α/2 is the critical t-value from the t-distribution with n−1 degrees of freedom.

• S is the sample standard deviation (since the population standard deviation σ\sigmaσ is unknown).

• S/sqrt(n)​ is the standard error of the mean.

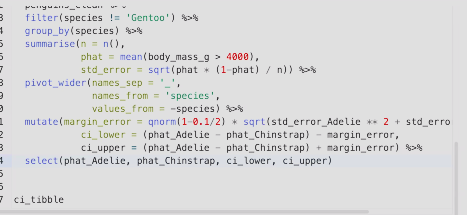
CI difference in proportions

t-dist code

Comparison between construction of CI with and without known sigma

1. 95% corresponds to 1.98 in a t-dist. since the area becomes n-1 = 99

   1. so then z score moves down

2. t_critical <- qt(0.975, df)