Quantum Theory and Electronic Structure of Atoms

Emission Series | Dual Nature of the Electron | Quantum Mechanics | Quantum Numbers | Atomic Orbitals

Lyman Series

Emission Series in the H Atom:
n = 1

Balmer Series

Emission Series in the H Atom:
n = 2

Paschen Series

Emission Series in the H Atom:

n = 3

Brackett Series

Emission Series in the H Atom:
n = 4

Ultraviolet

What is the Spectrum Region of the Series:

Lyman

Visible and Ultraviolet

What is the Spectrum Region of the Series:

Balmer

Infrared

What is the Spectrum Region of the Series:

Paschen

Infrared

What is the Spectrum Region of the Series:

Brackett

Standing Waves

Electrons, when considered as waves, can be described as (answer) within the atom, specifically around the nucleus.

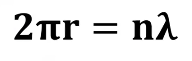
Equation for the Dual Nature of the Electron

De Broglie

Stated that waves can behave like particles and particles can behave like waves.

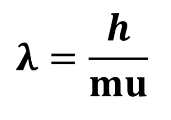
De Broglie’s Equation

Heisenberg Uncertainty Principle

There's a limit to how precisely certain pairs of physical properties of a particle, like position and momentum, can be known simultaneously.

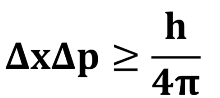
Heisenberg Uncertainty Principle Equation

Change in Position

What does the Δx in the Heisenberg Uncertainty Principle Equation stand for?

Change in Momentum

(mass x velocity)

What does the Δp in the Heisenberg Uncertainty Principle Equation stand for?

Orbitals

In Quantum Mechanics, what do you call the orbits?

Electron Density

In Quantum Mechanics, what do you call the Electron?

solid particle; NOT solid particles

With Bohr, Electrons are treated like a (answer). In Quantum Mechanics, particles are (answer).

Schrödinger Equation

A fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes over time.

Psi (𝚿)

Symbol for Wave Function

Electron Density

If you get the 𝚿², you will get the…?

Quantum Numbers

Describes the distribution of Electrons in an atom; they are derived from solving the Schrödinger Equation for the Hydrogen atom.

Principal Quantum Number (n)

Points to which orbital is occupied by an electron; n = 1, 2, 3,….

Angular Momentum Quantum Number (l)

Tells us the shape of an orbital located in n; l = 0 to (n-1)

Magnetic Quantum Number (m_l)

Describes an orientation in space of the orbital in space (which orbital); -l, (-l + 1),…, 0 , (+l - 1), +l

Electron Spin Quantum Number (m_s)

Points to one of the two electrons that can occupy an orbital in a specific subshell in a specific shell; m_s = -1/2, +1/2

Node

A region within a quantum mechanical system, such as an atom, where the probability of finding an electron is zero.