linear quiz/ test 3

FALSE: if A and B are row equivalent then they have the same eigenvalues

FALSE: if A and B are row equivalent then they have the same eigenvalues

not true

geometric multiplicity is ALWAYS

LESS THAN OR EQUAL TO THE ALGEBRAIC MULT.

algebraic multiplicity

number of times an eigenvalue repeats. Or the number of times that a root appears in the characteristic polynomial.

geometric multiplicity

dimension of eigenspace (also equal to number of free variables)

Diagonalizable

A square matrix A is said to be diagonalizable if A is similar to a diagonal matrix, that is, if A = PDP^-1 for some invertible matrix P and some diagonal matrix D

- a matrix is diagonalizable if the dimensions of its eigenvalues add up to the number of its columns AND rows??? (idk if its just columns and rows or both) see last question in 4.4 on page 4 titled the diagonalization theorem!!! for a great example

Know That

the eigenvalues of a triangular matrix are the numbers that go down diagonally

the sum of the algebraic multiplicities is equal to the

number of rows and columns that the corresponding matrix has and should also equal the degree of the matrix's characteristic polynomial

When the algebraic multiplicity is equal to 1 the geometric multiplicity is ALWAYS ALSO

EQUAL TO 1

know that when a matrix is linearly INDEPENDENT AKA INVERTIBLE...

0 can NOT be on of its eigenvalues

on the contrary, when a matrix is linearly DEPENDENT, AKA NOT INVERTIBLE

0 CAN be one of its eigenvalues 4.3 pg 3

Eigenvalue

A scalar lambda such that Ax = lamba x has a solution for some nonzero vector x

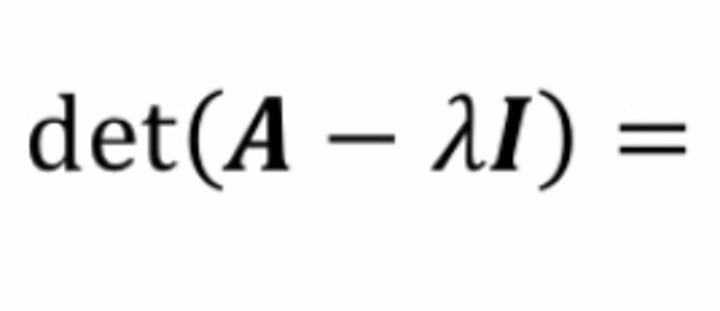
eigenvector

a nonzero vector x such that Ax = lambda(x) for some scalar lambda

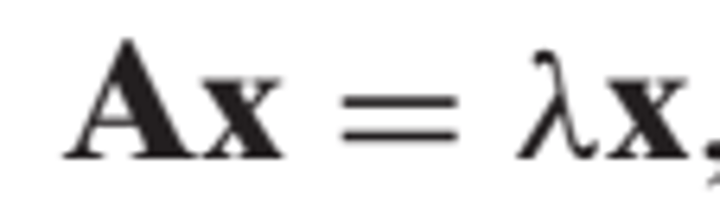
FOR a matrix to be DIAGONALIZABLE, the number of TOTAL eigenvectors (add up the dimension of each eigenvalue) should equal up to the number of rows and columns

i.e. if you get 3 total eigenvectors for a matrix with 3 rows and 3 columns then that matrix is DIAGONALIZABLE!!!

(A hint for this is if a matrix has all different # eigenvalues, you can tell that it will have the same # of distinct eigenvalues which will add to the # of rows and columns naturally) 4.4 pg. 3

remember that the D matrix should correspond to the P matrix, the D matrix just writes

the D matrix just writes out the eigenvalues diagonally surrounded by all zeros.

A diagonalizable matrix has an algebraic multiplictity EQUAL TO its geometric multiplicity

read again 4.4 pg 4

PLEASE DONT FORGET UR AUG. Matrixes

DONT FORGET TO WRITE UR BASIS AS { } and ur EIGENSPACE AS =span ([ ]) !!!! READ CAREFULLY AND USE CORRECT NOTATION

How to find the degree of a polynomial

to find the degree of a polynomial you add up the total of EVERY exponents (even the 1)

(1 + ¥)^3 (1-¥)^2 (¥ - 2) = 3 + 2 + 1 = 6 EXPONENTS

how do I know that I am working with a complex eigenvector???

You'll know bc the characteristic polynomial you get will be impossible to factor (there's no values that multiply to 5 and add up to 4) and you'll have to resort to the quadratic formula

ex: (¥^2 - 4¥ + 5) is impossible to factor and doing the quadratic formula out gives its complex eigenvalues

The det (A^T) is equal to the regular det(A)

the determinant of the TRANSPOSE and the determinant of the regular A matrix ARE THE SAME

Thm. 4.18 : if A is INVERTIBLE, integer ^k is automatically an eigenvalue of A^k w/ corresponding eigenvector x

if A is invertible and for example equal to A^-1, then ¥^-1 is automatically an eigenvalue for A^-1

KNOW THAT A CAN BE SUBSTITUTED FOR A #/ eigenvalue!!!!

Additional problems #2

show that -¥ (bar over lambda) is an eigenvalue of A

Know that -Ais equal to regular matrix A (SEE PHOTOS)

orthogonal

vectors that equal zero when multiplied together (dot product is zero)

how to check if something is orthonormal

A list of vectors is called orthonormal if each vector is:

1) orthogonal (dot product equals out to zero)

AND 2) each vector has a length of 1

if you ever have a test question asking what the dot product of two vectors in the same sub space is, the answer is ALWAYS zero

!!!! likely will be a MCQ (see pg. 3 of 5.2)

WHEN y is in the subspace, your answer for the orthogonal projection of y onto (W for example) WILL BE A LINEAR COMBINATION

see pg 2 5.2

"find the orthogonal projection of y onto W"

y= (y•u1/ u1•u1)(u1) + (y•u2/u2•u2) (u2) see pg 2 of 5.2

"find a basis for W__|__ "

being asked to find a basis for the col (A __|__) AKA write the basis for the column space of the TRANSPOSE see pg 2 of 5.2

An orthogonal basis for a subspace W of R^n is

a basis for W that is also an orthogonal set ( vectors are proven to be an orthogonal set when their dot products equal out to zero, them equaling out to zero proves that the vectors are l.i. And in turn, when the # of vectors matches the dimension of the span i.e. 3 l.i. vectors in R^3, the vectors must be a basis for R^3 ) see pg 1 of 5.1

vectors must be LINEARLY INDEPENDENT in order to make up an orthogonal basis for R^n

- a linearly dependent vector like the zero vector can't be among the vectors

- the vectors can't equal each other when multiplied together

Question: find the orthogonal decomposition of W

Y= (y-^y) +y (use given y - found y hap, plus given y

!!!!KNOW THAT THE INVERSE OF AN ORTHOGONAL MATRIX/SET OF VECTORS IS THE SAME AS ITS TRANSPOSE

IF YOU’RE ASKED TO WRITE THE INVERSE OF A MATRIX AND YOU ALR KNOW THAT IT IS ORTHOGINAL, THEN WRITE ITS TRANSPOSE AS THE ANSWER

the basis of a SPAN MUST HAVE THE EXACT SAME # OF VECTORS AS THE SPAN CALLS FOR

if asked for basis for span R², you better write a basis with exactly TWO VECTORS (the basis is different than the span and doesn’t need a minimum of i.e. 2 vectors like the span does but instead needs exactly 2 vectors!!!)

The conjugate of a complex eigenvalue is also another eigenvalue of the same vector!!!! i.e.(1+2i) and (1-2i) are both eigenvalues of the same vector

basically saying that a vector with eigenvalue (1+2i) also has (1-2i) as an eigenvalue bc they are the SAME THING

for a linearly independent matrix

the equation Ax=0 has only the trivial solution