Chapitre 4 : Caractéristiques des méthodes de dosage

I. Inexactitude

I. Inexactitude

Qu’est-ce que l’inexactitude dans une méthode de dosage ?

• C’est l’incapacité d’une méthode analytique à produire une valeur proche de la vraie valeur

• Tout résultat obtenu n’est pas nécessairement la valeur réelle

• La vraie valeur ne peut être obtenue que par une méthode de référence

Comment appelle-t-on la différence entre une valeur obtenue et la valeur de référence ?

Cette différence est appelée le biais

Quels sont les deux types de biais pouvant affecter une méthode analytique ?

• Biais constant

• Biais proportionnel

Qu’est-ce qu’un biais constant ?

• Il y a toujours la même différence fixe entre la valeur obtenue et la vraie valeur

• Exemple :

  • Si biais constant = 2 ng/mL

  • Valeur vraie = 10 ng/mL → valeur obtenue = 12 ng/mL → écart = 20%

  • Valeur vraie = 100 ng/mL → valeur obtenue = 102 ng/mL → écart = 2%

Quelle est la cause habituelle d’un biais constant ?

• Manque de spécificité de la méthode

• Une autre substance que l’analyte d’intérêt produit un signal parasite constant

  • Cette substance est présente à une concentration relativement stable dans tous les échantillons

Qu’est-ce qu’un biais proportionnel ?

• L’erreur est proportionnelle à la concentration réelle de l’analyte

• L’écart augmente avec la concentration

Donne un exemple illustrant un biais proportionnel.

• Biais proportionnel = 30 %

  • Si valeur vraie = 10 ng/mL → valeur obtenue = 13 ng/mL

  • Si valeur vraie = 100 ng/mL → valeur obtenue = 130 ng/mL

• L’erreur absolue augmente avec la concentration

Quelle est la cause habituelle d’un biais proportionnel ?

• Problème de calibration

• La valeur assignée au calibrateur par le fabricant ne correspond pas à la valeur réelle

Est-il possible qu’une méthode présente les deux types de biais ?

• Oui, les biais constant et proportionnel ne sont pas exclusifs

• Une méthode peut cumuler les deux types de biais en même temps

Quel rappel mathématique illustre l’association des deux biais ?

• Équation d’une droite :

y=ax+b

• a = pente → reflète le biais proportionnel

• b = intercept à l’origine → reflète le biais constant

Comment compare-t-on une méthode de dosage à une méthode de référence ?

• En réalisant une régression linéaire entre :

  • Les résultats de la méthode utilisée (axe Y)

  • Les résultats de la méthode de référence (axe X)

Quelle est la forme idéale de la droite de régression en absence de biais ?

• Une droite parfaite de pente = 1 et intercept = 0

• Angle de 45°

• Équation :

  Y=1X+0

Que signifie un biais constant sur un diagramme de régression ?

• La droite est parallèle à la droite idéale

• L’intercept (b) est différent de 0

• L’équation devient :

  Y=1X+b

  • b = valeur du biais constant

Que signifie un biais proportionnel sur un diagramme de régression ?

• Plus la concentration augmente, plus la différence entre les deux méthodes augmente

• L’intercept = 0, mais la pente (a) est différente de 1

• Équation :

  Y=aX+0

  • a < 1 → biais négatif proportionnel

  • Exemple : a = 0.8 → biais de -20%

Quel est l’effet d’un biais proportionnel de 20 % ?

• La méthode testée donne des valeurs égales à 80 % de la méthode de référence

• Et cela à toutes les concentrations

Pourquoi les coefficients a et b peuvent-ils varier d’un échantillonnage à l’autre ?

• Parce que chaque échantillon présente une variabilité naturelle

• Exemple :

  • 40 échantillons → Y = aX + b

  • 40 autres échantillons → Y = a′X + b′

  • 50 échantillons → Y = a″X + b″

• C’est pourquoi on fournit toujours a et b avec un intervalle de confiance à 95 %

Que signifie un intervalle de confiance à 95 % pour la pente ou l’intercept ?

• C’est l’étendue des valeurs que prendraient a et b si l'on dosait un nombre infini d’échantillons

• Il y a 95 % de chances que :

  • La pente réelle soit comprise dans l’intervalle donné

  • L’intercept réel soit compris dans son propre intervalle

Exemple d’équation de régression avec intervalle de confiance ?

• Équation :

  Y=0,97X+1,5

• Intervalle de confiance de la pente : [0,92 ; 1,02]

• Intervalle de confiance de l’intercept : [-0,5 ; 3,5]

Comment interpréter ces intervalles de confiance ?

• Si l’intervalle de la pente contient 1, → on ne peut pas conclure à un biais proportionnel

• Si l’intervalle de l’intercept contient 0, → on ne peut pas conclure à un biais constant

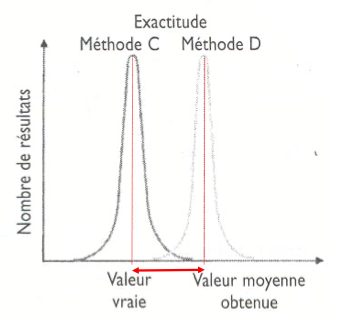
Comment représente-t-on graphiquement un biais ?

• La valeur vraie est représentée au centre d’une distribution gaussienne

• Même si elle est obtenue par une méthode de référence, il y a une variabilité naturelle autour

• Le biais est la différence entre :

  • La valeur obtenue avec la méthode de dosage

  • Et la valeur de référence

    

Calcul du biais en pratique

Calcul du biais en pratique

Combien existe-t-il de méthodes pour calculer un biais ?

Il en existe trois

• Sur base de contrôles externes

• Sur base d’échantillons certifées

• Avec plusieurs dosages sur la méthode à déterminer et la méthode considéré comme méthode de référence

1ʳᵉ méthode : comment calcule-t-on le biais avec des contrôles externes ?

• Le laboratoire reçoit un échantillon de concentration inconnue

• Il le dose et envoie le résultat à l’organisme externe

• L’organisme compare le résultat à la moyenne des utilisateurs utilisant la même trousse ("pairs")

• Cela donne un biais relatif, car la valeur exacte n’est pas connue

Quand un biais absolu peut-il être calculé à partir d’un contrôle externe ?

• Lorsque la valeur de l’échantillon est connue grâce à une méthode de référence

• Le résultat est comparé directement à la valeur de référence → c’est un biais absolu

Peut-on toujours calculer un biais absolu ?

• Non

• Cela dépend de l’existence d’une méthode de référence pour l’analyte concerné

2ᵉ méthode : comment calcule-t-on le biais avec des échantillons certifiés ?

• Un laboratoire de référence dose plusieurs échantillons (ex : 10)

• Un autre laboratoire achète ces échantillons

• Il les dose avec sa propre méthode

• Il compare ses résultats à ceux fournis par le labo de référence

• Cela permet de calculer un biais exact

Quelle est la formule générale de calcul du biais (en %) ?

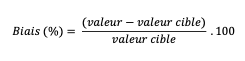
Le biais peut-il être positif ou négatif ?

• Oui

  • Positif : la méthode surestime la concentration

  • Négatif : la méthode sous-estime la concentration

Examen bien mettre biais positif ou négatif

Calcul du biais à l’aide d’un contrôle externe

Calcul du biais à l’aide d’un contrôle externe

Quel est l’exemple donné pour illustrer le calcul du biais à l’aide d’un contrôle externe ?

Le contrôle DEQUAS pour le dosage de la 25(OH)-D (vitamine D)

Dans le premier exemple (sans méthode de référence), que montrent les résultats des utilisateurs DiaSorin Liaison Total ?

• Une belle distribution gaussienne autour de la moyenne

• Le résultat du laboratoire : 60 nmol/mL

• Moyenne des utilisateurs DiaSorin : 61,4 nmol/mL

• Moyenne ALTM (All Laboratory Trimmed Mean) : 68,8 nmol/mL (moyenne de toutes les méthodes ayant participé au contrôle)

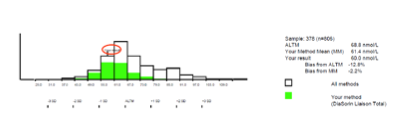
Quel est le biais du laboratoire par rapport aux autres utilisateurs DiaSorin ?

-2,2 % (biais négatif)

Quel est le biais du laboratoire par rapport à l’ALTM ?

-12,8 %

Peut-on conclure à un biais absolu dans ce cas ? Pourquoi ?

• Non, car il n’existait pas encore de méthode de référence pour assigner une valeur vraie au contrôle

• L’ALTM ne peut pas être considérée comme une valeur de référence fiable

• Elle est influencée par les méthodes les plus utilisées sur le marché

Que montre la distribution des résultats DiaSorin par rapport aux autres méthodes ?

• Une orientation vers la gauche → indique un petit biais négatif

Que montre le deuxième contrôle DEQUAS (juillet 2018) ?

• Il est effectué avec une méthode de référence pour déterminer la valeur cible

Quelle est la valeur de référence dans ce deuxième contrôle ?

• 72,6 nmol/L

Quelle est la valeur ALTM lors de ce deuxième contrôle ?

80,6 nmol/L

Que montre la comparaison entre l’ALTM et la valeur de référence ?

• L’ALTM présente un biais positif → elle surestime la concentration réelle

• Cela confirme que l’ALTM n’est pas une cible fiable

Quel est le résultat du laboratoire avec la méthode DiaSorin lors du deuxième contrôle ?

88,3 nmol/L

Quel est le biais absolu du laboratoire par rapport à la valeur de référence ?

+21,6 %

Quel type de biais est observé ici ?

• Un biais positif important

• Le laboratoire est biaisé vers la droite par rapport à ses pairs

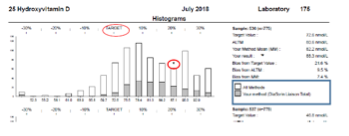
Pourquoi ces résultats sont-ils plus informatifs que les précédents ?

• Parce qu’ils s’appuient sur une valeur cible fiable issue d’une méthode de référence

• Ils donnent une véritable photographie du biais absolu

Quel est le résultat du laboratoire utilisant une seconde méthode (LC-MS/MS) ?

• Résultat exactement sur la cible

• Biais absolu : -0,1 %

Quelle conclusion peut-on tirer de la méthode LC-MS/MS ?

• Elle présente un biais négligeable

• Elle est beaucoup plus précise et fidèle que la méthode DiaSorin dans cet exemple

Calcul du biais à l’aide d’échantillons certifiés pas vu

Calcul du biais à l’aide d’échantillons certifiés

Quel programme est cité comme exemple de calcul du biais à l’aide d’échantillons certifiés ? pas vu

• Le Vitamin D Standardization Certification Program (VDSCP)

• Fourni par le CDC

Comment fonctionne ce programme de certification ? pas vu

• Tous les 3 mois, le laboratoire reçoit 10 échantillons

• Ces échantillons sont certifiés par méthode de référence du CDC

• Le laboratoire les dose en double sur 2 jours (4 mesures par échantillon)

• Les résultats moyens sont comparés à la valeur cible (Target) définie par le CDC

• Le biais (%) est calculé pour chaque échantillon

Quel est le biais moyen observé dans cet exemple ? pas vu

• +6,56 %

• Il s’agit d’un biais positif

Quelle est la limite de biais acceptable dans ce programme ? pas vu

5 % maximum

Que faut-il envisager si le biais dépasse cette limite ? pas vu

• Il faut revoir la calibration de la méthode de dosage

 Calcul du biais à l’aide d’une comparaison de méthode pas vu

 Calcul du biais à l’aide d’une comparaison de méthode

Quelle autre méthode permet de comparer deux méthodes de dosage ?

pas vu

• Une comparaison de méthode sur une série d’échantillons patients

Comment se déroule une comparaison de méthode ? pas vu

• On sélectionne environ 40 échantillons patients

• Ils couvrent toute la gamme de concentrations

• Chaque échantillon est dosé :

  • En double

  • Avec la méthode testée (axe Y)

  • Et avec la méthode de référence (axe X)

Quelle régression statistique utilise-t-on dans ce cas ?

La régression selon Passing-Bablok

Comment interprète-t-on les résultats de la régression Passing-Bablok ?

• On calcule :

  • La pente (a) avec un intervalle de confiance à 95 %

  • L’intercept (b) avec un intervalle de confiance à 95 %

Que signifie un intervalle de confiance de la pente contenant 1 ?

• On ne peut pas conclure à un biais proportionnel significatif (95% de chance qu’il ne soit pas significatif)

Que signifie un intervalle de confiance de l’intercept contenant 0 ?

• On ne peut pas conclure à un biais constant significatif (95% de chances qu’il ne soit pas significatif)

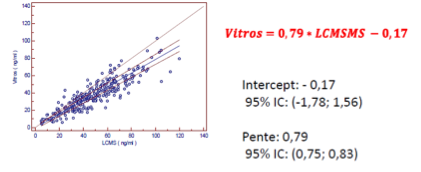
Donne un exemple de régression Passing-Bablok appliquée à la vitamine D.

• Méthode testée : immunodosage Vitros

• Méthode de référence : LC-MS/MS

• Équation de régression :

  

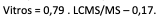
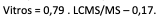
Comment interprète-t-on les intervalles de confiance dans cet exemple ?

• IC de l’intercept : [-1,78 ; 1,56] → contient 0 → pas de biais constant significatif

• IC de la pente : [0,75 ; 0,83] → ne contient pas 1 → présence d’un biais proportionnel

Quel est le biais proportionnel observé dans cet exemple ?

La méthode Vitros sous-estime la concentration d’environ 21 % par rapport à la LC-MS/MS

Que montre un exemple de régression où Y = X avec l’IC de la pente incluant 1 et l’IC de l’intercept incluant 0 ?

• Il n’existe ni biais proportionnel, ni biais constant

• La méthode testée est équivalente à la méthode de référence

Qu’est-ce que le diagramme de Bland-Altman ? pas vu

• Un outil graphique utilisé pour comparer deux méthodes de mesure

• Permet de visualiser la différence individuelle entre deux méthodes pour chaque échantillon

Comment sont représentées les données dans un diagramme de Bland-Altman ? pas vu

• Axe des Y :

  • Différence entre les deux méthodes (ex : Vitros – LC-MS/MS)

• Axe des X :

  • Moyenne des deux méthodes pour chaque échantillon

Que montre ce diagramme dans l’exemple Vitros vs LC-MS/MS ? pas vu

• Le Vitros donne des valeurs plus basses que la LC-MS/MS

• La différence moyenne entre les deux méthodes est de –10,6 ng/mL

• La majorité des points sont en dessous de la ligne 0, indiquant un biais systématique

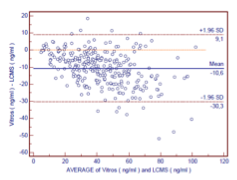
Quel est l’intervalle de confiance à 95 % pour cette différence moyenne ? pas vu

• Entre +9,1 ng/mL et –30,3 ng/mL

• Cet IC est large, ce qui traduit une variabilité importante

Comment interpréter la répartition des valeurs sur le diagramme ? pas vu

• Plus les concentrations augmentent, plus les points s’éloignent de la moyenne

• Cela indique un biais proportionnel (l’erreur augmente avec la concentration)

  

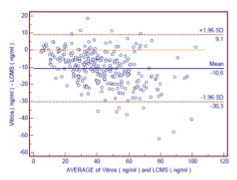
À quoi devrait ressembler un diagramme de Bland-Altman idéal (sans biais) ?

• Les points devraient être répartis de part et d’autre de la ligne 0

• La moyenne des différences devrait être proche de 0

• Il ne devrait pas y avoir de tendance avec l’augmentation des concentrations

Comment corriger un biais ?

Comment corriger un biais ?

Un biais doit-il être accepté comme normal ?

• Non

• Un biais ne devrait pas exister

• Lorsqu’on le détecte, il faut prendre des mesures pour le corriger

Comment corriger un biais proportionnel ?

• C’est généralement plus facile à corriger

• Souvent lié à un problème de calibration

• Exemple :

  • Pour le Vitros, biais proportionnel de –20 %

  • Cause : les calibreurs ne sont pas bien étalonnés par rapport à la méthode de référence

  • Solution : réassigner la concentration des calibreurs → par exemple, augmenter leur valeur de 20 %

Comment corriger un biais systématique ?

• C’est beaucoup plus compliqué

• Cause fréquente :

  • Interférence dans le sérum

  • Manque de spécificité de la méthode

  • Une substance inconnue produit un signal constant

• Solution :

  • Repenser la méthode

  • Trouver et éliminer la source d’interférence

Peut-on cumuler un biais proportionnel et un biais systématique ?

• Oui

• Les deux types de biais peuvent s’additionner entre une méthode de routine et une méthode de référence

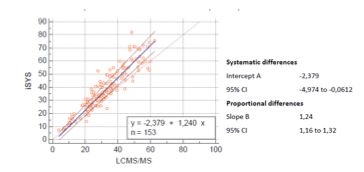
Donne un exemple où les deux biais coexistent.

• Équation Passing-Bablock pour la méthode iSYS comparée à la LC-MS/MS :

  y=1,24x−2,379

• Interprétation :

  • Intercept ≠ 0 → biais systématique

  • Pente ≠ 1 → biais proportionnel

  • Les intervalles de confiance ne contiennent ni 0 ni 1, confirmant les biais

Que faut-il faire face à une méthode qui cumule les deux biais ?

• Revoir la calibration pour corriger le biais proportionnel

• Améliorer la spécificité de la méthode pour réduire le biais systématique

II. Imprécision

II. Imprécision

Qu’est-ce que l’(im)précision ?

• C’est la capacité d’obtenir des résultats reproductibles

• Elle reflète la variabilité due aux erreurs aléatoires

Comment calcule-t-on l’imprécision d’une méthode de dosage ?

• En divisant l’écart-type (SD) par la moyenne (x̄)

• Puis on multiplie par 100 pour obtenir le coefficient de variation (CV)

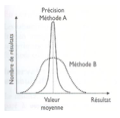
Que montre la comparaison entre deux méthodes A et B avec la même moyenne ?

• Méthode A : écart-type plus faible → CV plus faible → meilleure précision

• Méthode B : écart-type plus élevé → CV plus élevé → précision moins bonne

Quand calcule-t-on traditionnellement le coefficient de variation ?

Lors de la validation d’une nouvelle méthode

Que recommandent les Guidelines CLSI pour valider une nouvelle méthode ?

• Sélectionner 5 échantillons de valeurs différentes

• Les doser 5 fois de suite pendant 5 jours consécutifs

• Résultat : 25 mesures par échantillon

Quels types d’écarts-types calcule-t-on lors de cette validation ?

• Écart-type intra-jour : variation dans la même journée

• Écart-type inter-jour : variation d’un jour à l’autre

Quelle méthode statistique est utilisée pour évaluer ces variations ?

L’ANOVA (Analyse de la Variance)

Quelle autre manière existe-t-il pour évaluer l’imprécision au quotidien ?

Utiliser les contrôles internes du laboratoire

Pourquoi est-il intéressant de calculer le CV sur les contrôles internes ?

• Car cela reflète la variabilité réelle dans le temps

• Facteurs affectant la précision au quotidien :

  • Vieillissement de la machine

  • Changement de lots de réactifs

  • Aiguilles partiellement bouchées (fibrine)

  • Vieillissement des sources lumineuses

Pourquoi le CV sur 5 jours est-il moins représentatif ?

• Il ne montre que la performance sur une courte période

• Il ne prend pas en compte les variations à long terme

Que permet de vérifier le CV des contrôles internes ?

Que les résultats sont corrects, constants et reproductibles au cours du temps réel d’utilisation

Exemples

Exemples

Donne un exemple de validation multicentrique d’une nouvelle trousse de dosage.

• Validation de la trousse PINP (marqueur de formation osseuse)

• Trois laboratoires impliqués :

  • Danemark

  • Grande-Bretagne

  • Belgique

• Chaque labo utilise sa propre machine

Comment les échantillons sont-ils testés dans cet exemple ?

• Deux échantillons envoyés à chaque laboratoire

• Chaque labo réalise 5 dosages par jour pendant 5 jours

• Total : 25 valeurs par pays → 75 valeurs au total

Comment sont analysés les résultats ?

ANOVA réalisée pour évaluer la variation :

• Selon le jour → donne variation inter-jour et intra-jour

• Selon le pays → donne variation inter-pays et intra-pays

Quels sont les résultats pour la variation selon le jour ?

• Moyenne des 75 valeurs : 30,57 µg/L

• Écart-type inter-jour : 2,47 µg/L

• Écart-type intra-jour : 1,55 µg/L

• CV inter-jour : 8,1 %

• CV intra-jour : 5,1 %

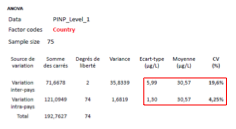
Quels sont les résultats pour la variation selon le pays ?

• CV inter-pays : 19,6 % (plus grande variabilité entre pays)

• CV intra-pays : 4,25 %

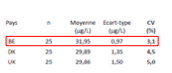
Que montre le détail pour la Belgique ?

• Moyenne plus élevée : 31,95 µg/L

• CV plus petit : 3,1 %

• Indique une bonne précision interne

Comment peut-on évaluer la reproductibilité d’une méthode en pratique quotidienne ?

• Grâce aux contrôles qualité internes

Donne un exemple concret de contrôle interne pour le glucose.

• Utilisation d’un Abbott Alinity pour analyser le glucose

• Contrôle interne : échantillon Technopath

• Cet échantillon est dosé plusieurs fois par jour pour vérifier la stabilité des résultats

• Outil complémentaire : règles de Westgard pour surveiller les écarts

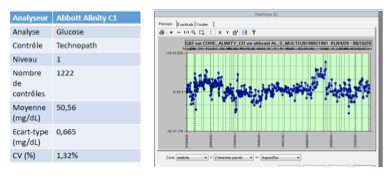
Quel est le résultat observé pour le CV sur les contrôles internes glucose ?

• Sur 1222 contrôles, le CV est de 1,32 %

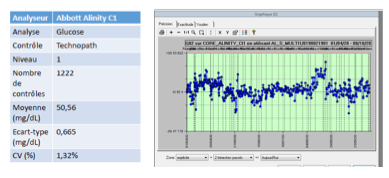
Que montre la carte de contrôle de qualité pour le glucose ?

• Un graphique avec tous les résultats successifs

• Visualisation des fluctuations et des dérives éventuelles

• Si dérive, cela peut entraîner un recalibrage de la machine

III. Combinaison de 2 types d’erreurs

III. Combinaison de 2 types d’erreurs