Chapter 13 - Network and Decision Mathematics
1/25
Earn XP
Description and Tags
Network and Decision Mathematics explained in a NUTSHELL.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
26 Terms
Network Key Terms
Graph: Diagram with points (vertices) connected by lines (edges).
Vertices/Nodes: Dots representing points on a graph.
Edges: Lines connecting vertices (can loop to itself).
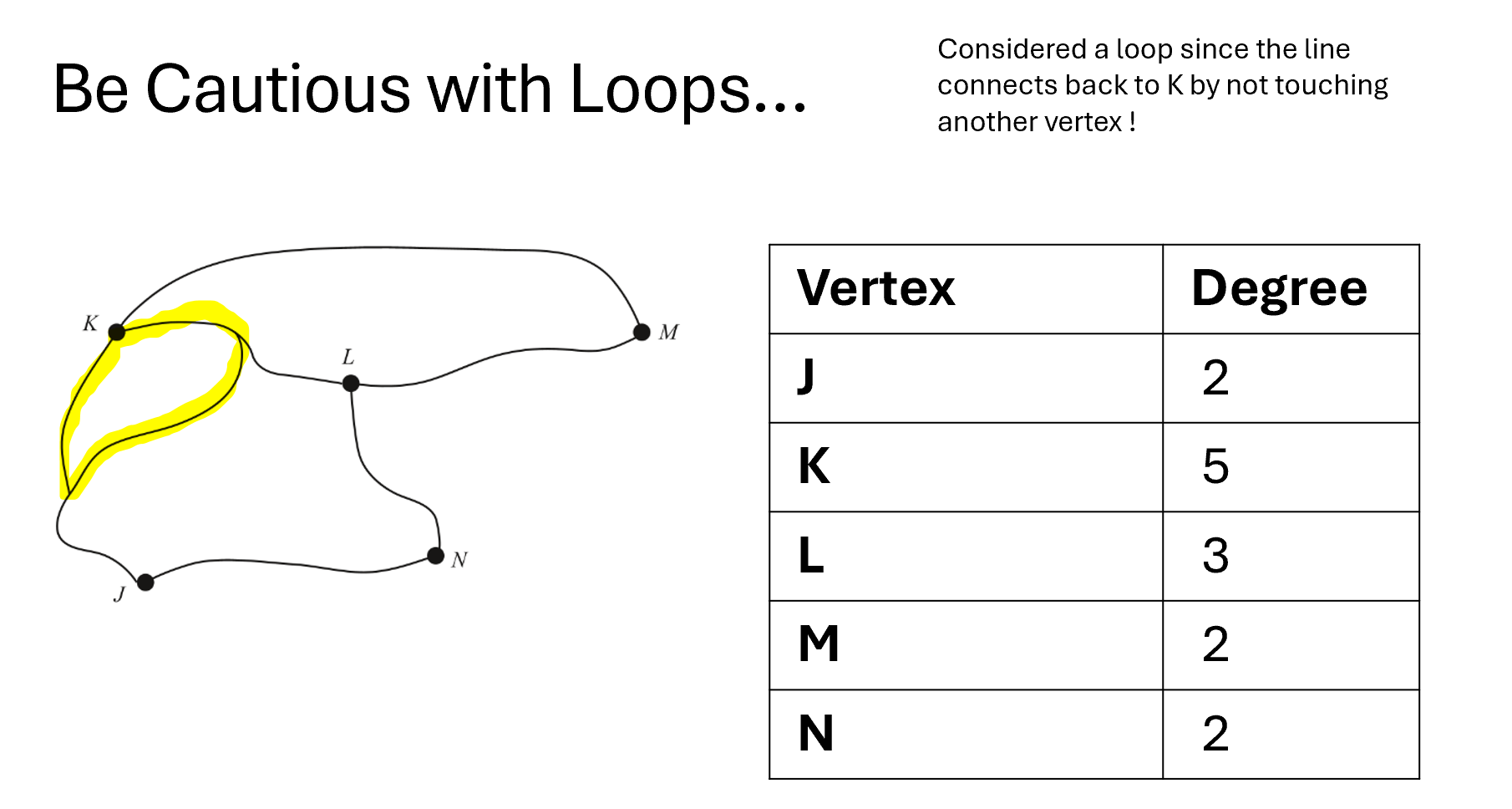
Loops: Edges that connect a vertex back to itself.
Degree of a Vertex
Degree of a vertex: the number of edges attached to a vertex.
Note: degree of a loop is 2 as the edge is attached twice to the vertex.
Types of Graphs
Type of Graph | Details | Example / Notes |
|---|---|---|
Simple Graph | No loops or multiple edges. | Sum of degrees = 2 × (number of edges) 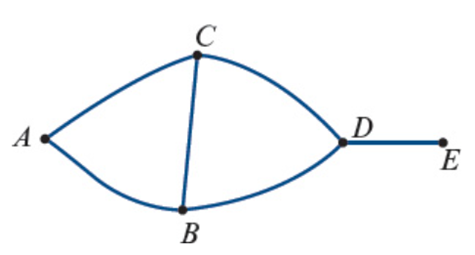 |
Isolated Vertex | A vertex with no connections. | Degree of Vertex = 0 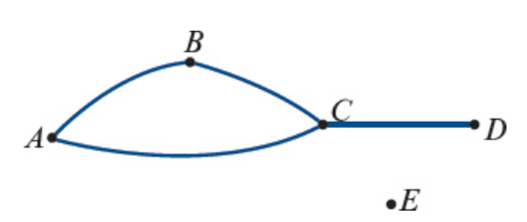 |
Degenerate Graph | All vertices are isolated (no edges at all). | Every vertex has degree 0 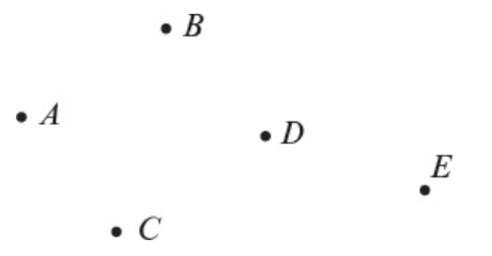 |
Further Types of Graphs
Type of Graph | Details | Formula (FYI only) | Notes / Examples |
|---|---|---|---|
Connected Graph | All vertices are connected directly or indirectly. | Max edges = (n(n−1))/2 | A bridge connects two separate parts. 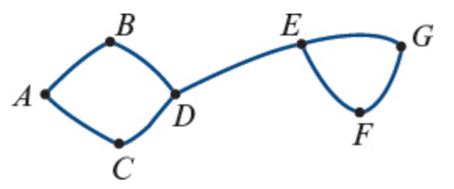 |
Complete Graph | Every vertex is connected to every other vertex. | Edges in Kₙ = (n(n−1))/2 | Notation: Kₙ, where n is number of vertices. 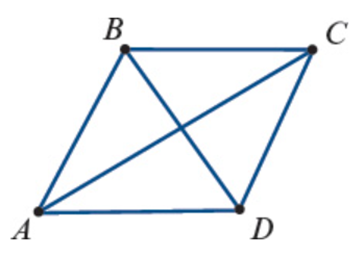 |
Subgraph | A smaller graph within a larger one. | – | Must include endpoints of chosen edges. 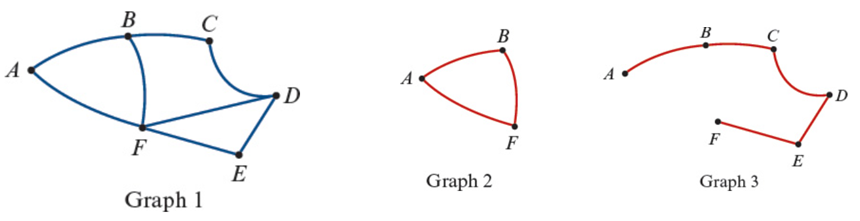 |
Even Further Types of Graphs
Type of Graph | Description | Example |
|---|---|---|
Undirected Graph | Edges work both ways between vertices (no arrows). | A–B is same as B–A 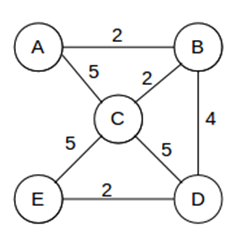 |
Directed Graph (Digraph) | Edges go one way only, shown with arrows. | A → B ≠ B → A 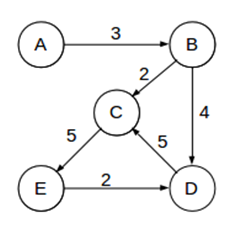 |
Cycle | A path that starts and ends at the same vertex, without repeating vertices/edges. | K–L–M–N–K or K–N–L–K 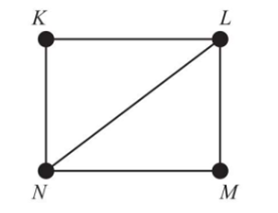 |
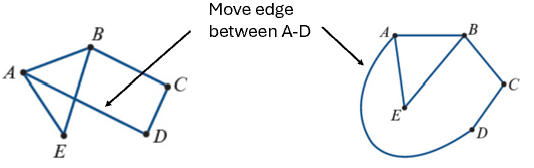
Equivalent (isomorphic) graphs
Isomorphic graphs: same structure, different layout.
Must have equal vertices and equal edges.
Matching vertex degrees is essential.
🔍 Tip: Write down degrees, then try redrawing to check!
Planar graphs
Planar graph: can be drawn without edges crossing.
Loops and multiple edges don’t affect planarity.
If not possible → it’s a non-planar graph.
Euler's formula (ONLY FOR PLANAR GRAPHS)

Faces
Faces: enclosed regions in a graph.
A loop counts as a face.
The outside space also counts as a face.
Must draw graph without crossing edges to spot faces (make it planar first to count faces!)
Adjacency Matrix
Adjacency matrix: n×n square matrix representing graph connections.
n = number of vertices.
0 = no edge between vertices.
1 = one edge; 2 = two edges, etc.
Loop: ‘1’ on the diagonal (vertex connected to itself).
Planar Graphs Summary
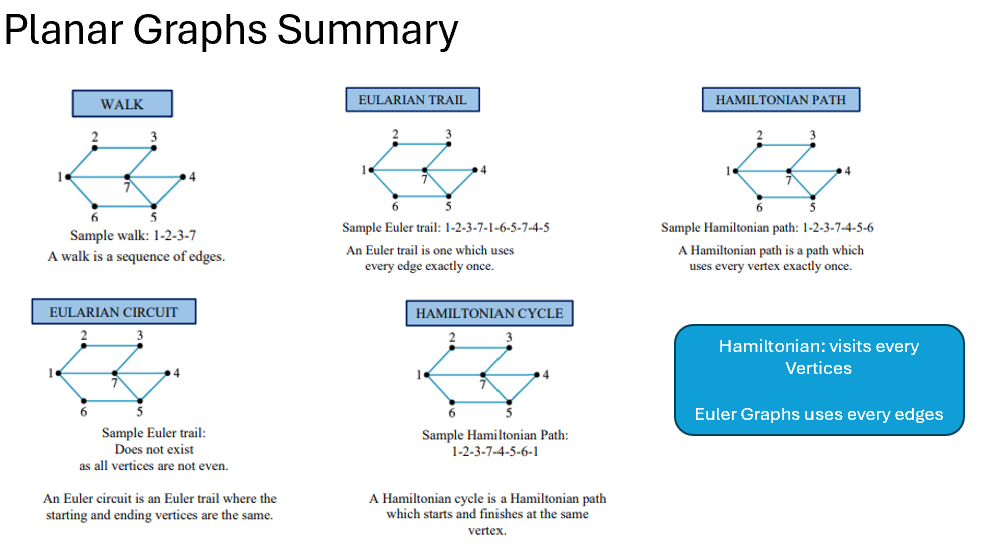
Describing and analysing planar graphs
Term | Definition | Key Rule | Example Idea |
|---|---|---|---|
Walk | Sequence of edges connecting vertices (repeats allowed) |
| Roaming a city; some places unreachable if not connected |
Exploring | Walk (trail or circuit) that travels every edge exactly once | Must use all edges once | Tracing every road once with no repeats |
Trail | Walk with no repeated edges; vertices can repeat | Don’t reuse edges | Walking streets without reusing roads |
Circuit | Trail that starts and ends at the same vertex | No edge repeats, same start/end | A loop that returns to the starting point |
Describing and analysing planar graphs: Exploring
Term | Definition | Rules (Conditions) | Example |
|---|---|---|---|
Eulerian Trail | A trail that uses every edge exactly once | • Graph is connected | Walking all streets once, starting at one odd-degree point and ending at the other |
Eulerian Circuit | An Eulerian trail that starts and ends at the same vertex | • Graph is connected | Mail loop covering every edge, returning to depot |
Fleury's Algorithm for Eulerian Trails or Circuits
Start:
If 2 odd-degree vertices, pick one of them.
If all even, pick any vertex.Travel:
Move along edges not bridges (unless forced).
Mark edges as you go.Repeat:
Keep traveling & marking until all edges are covered.
Describing and analysing planar graphs
Term | Definition | Example |
|---|---|---|
Travelling | Determining a walk (path/cycle) that visits each vertex exactly once. | Hamiltonian Path visiting all nodes |
Path | A walk with no repeated edges and no repeated vertices. | A → B → C without revisits |
Cycle | A path that starts and ends at the same vertex, no repeats. | A → B → C → A round trip |
Types of Hamiltonian Networks
Term | Definition | Condition (Rule) | Example |
Hamiltonian Path | A path that visits every vertex of a graph exactly once. | Not every edge has to be part of the path. Max two dead-end vertices (degree 1), which become start/end points. More than two dead ends? No Hamiltonian path. Vertices with degree 2 must use both their edges in the path or cycle. | Example Path: A → B → C → D |
Hamiltonian Cycle | A Hamiltonian path (visits every vertex once) that starts and ends at the same vertex. | •Not all edges need to be used in a Hamiltonian cycle | Example Cycle: A → B → C → A |
Eulerian vs. Hamiltonian—Focus
Eulerian = Edges
Trail = open walk (start ≠ end)
Circuit = closed loop (start = end)
Hamiltonian = Vertices
Path = open walk (start ≠ end)
Cycle = closed loop (start = end)
Weighted Graphs and Networks
Key Word | Definition | Example |
|---|---|---|
Weighted Graph | A graph where each edge has a number (weight) representing size of some quantity. | Weights can be distances, costs, or other measures. |
Network | A weighted graph where weights represent physical quantities like distance, time, or cost. | Distances in km between towns (vertices) in the graph. |
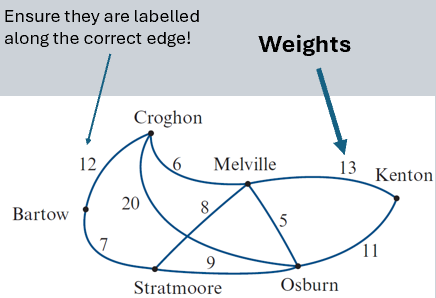
Shortest Path Problems
Goal: Find shortest path between two vertices.
Shortest path: Path with minimum total weight (sum of edges).
Method: List all possible paths from start to target vertex.
Shortcut: Ignore obviously long routes to save time.
Dijkstra’s Algorithm Overview
Finds shortest path with least total weight between two vertices.
Update vertex numbers only if smaller distance is found.
Once a vertex is circled (finalised), its number is locked forever.
No need to circle every vertex — stop when target’s reached or no better path exists.
Steps of Dijkstra's Algorithm
Assign starting vertex 0 and circle it.
For connected vertices, add edge weights to current number and write new values.
Circle the vertex with the lowest number.
Repeat steps 2–3 from newly circled vertex until destination is reached.
Backtrack from destination: find circled vertices where
current number = next number − edge weight.Repeat backtracking until you reach the start.
Dijkstra’s Method 2 - Optional (1-4)
Set up table:
Start vertex = first row.
Other vertices = columns.
Fill first row:
Put distances from start to each vertex.
Mark ✗ if no direct edge.
Find smallest number in row:
Circle/square it.
That column vertex becomes new row vertex.
Fill next row:
Add circled number + edge to column vertex.
If new sum ≤ number above, write it; else copy above.
If no connection, copy above or mark ✗.
Find smallest unmarked number:
Circle it.
That column vertex becomes new row vertex.
Copy circled numbers down.
Repeat steps 4 & 5 until destination column has a circle.
Shortest path length = circled number in destination column.
Find shortest path:
From destination, trace upward to same value in column.
Find corresponding row vertex, draw line to its column.
Repeat until start vertex row reached.
The horizontal lines = route.
Type of Trees (yes)
Keyword | Details | Key Notes | Example |
|---|---|---|---|
Tree | A connected graph with no circuits (no loops, multiple edges, or cycles). | If it has n vertices, edges e = v - 1. | 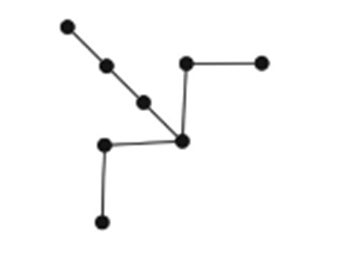 |
Spanning Tree (Subgraph) | A subgraph that is a tree connecting all vertices of the original graph. | Connects all vertices; no cycles. | 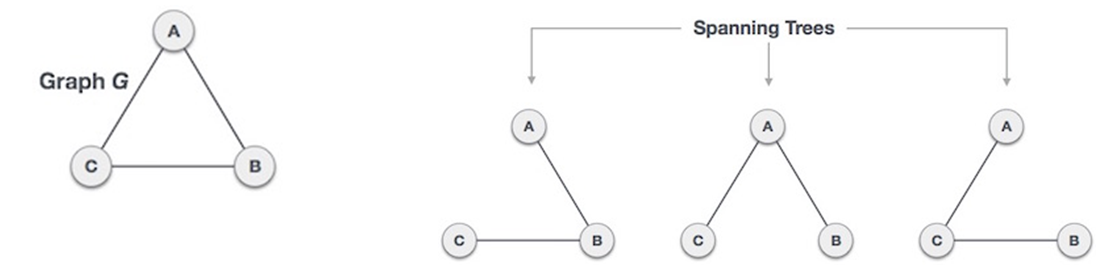 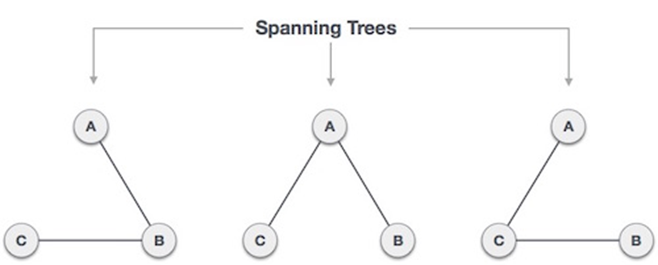 |
Minimum Spanning Tree | A spanning tree with the smallest possible sum of edge weights. | More than one MST can exist for a graph. | 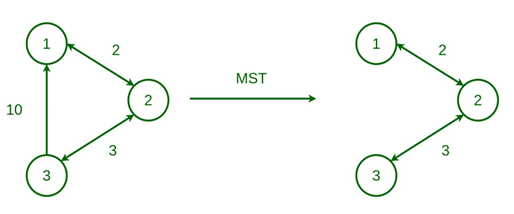 |
Finding the minimum spanning tree—Method 1: Greedy Algorithm (By Inspection)
Pick the smallest edges one by one.
Avoid edges that form a cycle.
Stop when all vertices are connected.
Finding the minimum spanning tree—Method 2: Prim’s Algorithm
Pick the smallest edge in the whole graph.
From connected vertices, pick the smallest edge leading out.
Keep picking the smallest edges from connected vertices that reach new vertices.
Repeat 3 until all vertices are connected.
Example Question:
A graph has five vertices: A, B,C, D and E. It has no duplicate edges and no loops. If this graph is complete, write down the adjacency matrix for the graph.
Adj(K5)=
0 1 1 1 1
1 0 1 1 1
1 1 0 1 1
1 1 1 0 1
1 1 1 1 0