14: Clustering: Kmeans and hierarchical

Is Euclidean distance always the best measure for assessing differences over time, or would a correlation-based approach sometimes be more appropriate?

Euclidean distance is useful when we are interested in the absolute magnitude of differences between observations over time. However, if the goal is to compare patterns of change rather than absolute values, a correlation-based measure may be more appropriate. Correlation focuses on whether two variables increase or decrease in a similar way over time, regardless of their scale. In many cases, particularly when studying trends or relationships, a correlation-based approach provides more meaningful insights than Euclidean distance.

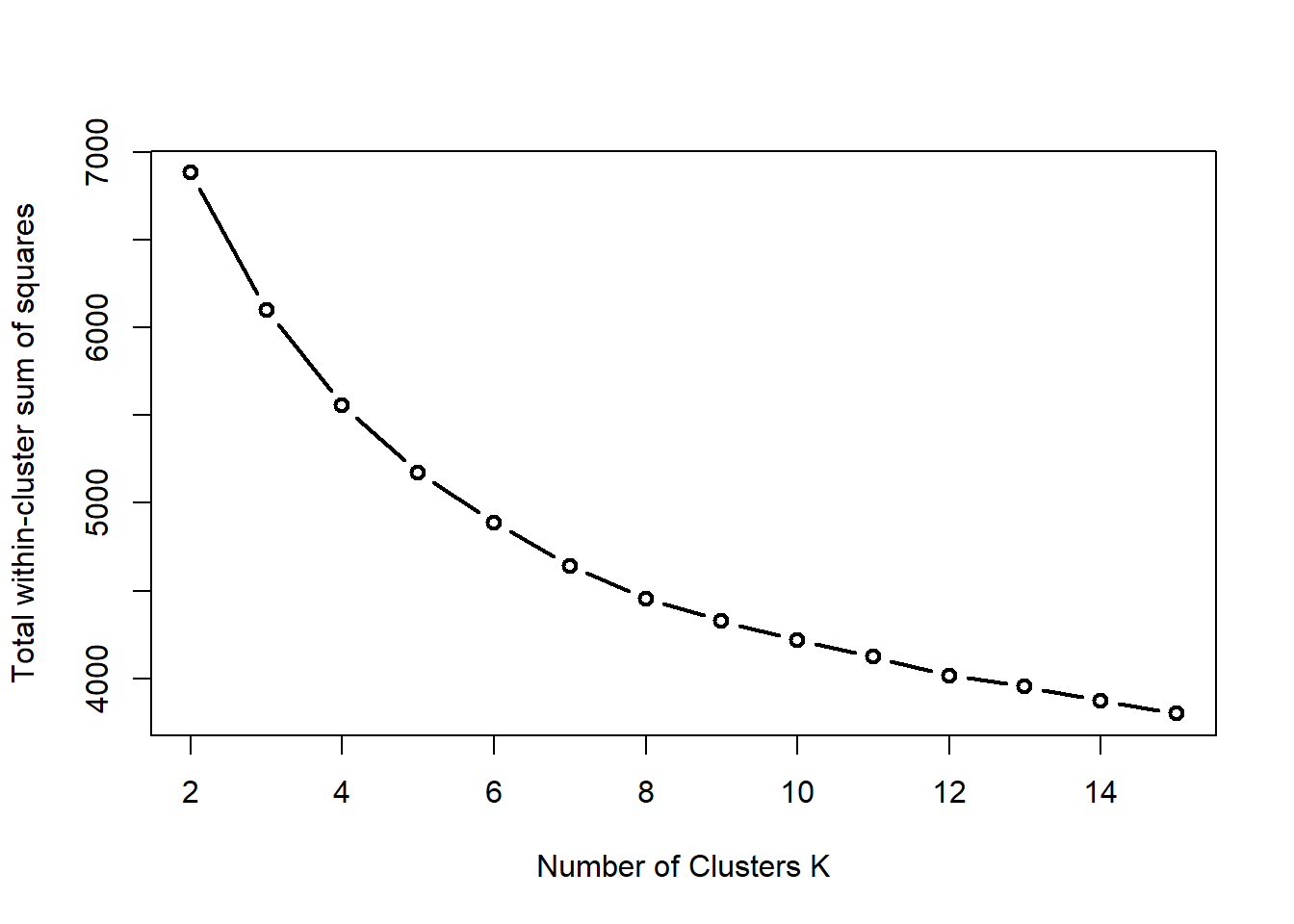
Explain this picture

5. We see that the total within-cluster variation decreases with the number of clusters. Typically, one looks for a kink in the total variation curve (or its logarithm) to locate the optimal number of clusters. Here there is no clear indication so other approaches need to be followed to choose a value for K.

Why do we use clustering?

As methods from unsupervised learning we would use them to get insights into variation and grouping structure in our data. We have seen that we can cluster based on observations, but also based on features/variables and can combine both clustering results together as shown in the example for gene expression data. Since clustering is an unsupervised learning method there is benchmark that we can compare the results with. Therefore one has to be careful how to report the results and they should not be taken or presented was the absolute truth. However, they can constitute a good starting point for further studies.

x