interspecific competition pt 2 (lotka/volterra equations->graphs)

logistic equation for population growth

dN/dt = rN(K-N/K)

dN

change in population size

dt

change in time

r

reproductive potential of the population

(birth rate - death rate)

N

population size

K

carrying capacity

(how many individuals the environment can support)

N₁ or βN₁

species 1

N₂ or αN₂

species 2

α

effect of species 2 on 1

β

effect of species 1 on 2

species 1 equation

dN₁/dt = r₁N₁(K₁-N₁-αN₂/K₁)

what is this equation telling you?

dN₁/dt = r₁N₁(K₁-N₁-αN₂/K₁)

in the absence of interspecific competition, α=0 and N₂=0 → the population of species 1 grows logistically at carrying capacity

species 2 equation

dN₂/dt = r₂N₂(K₂-N₂-βN₁/K₁)

what is this equation telling you?

dN₂/dt = r₂N₂(K₂-N₂-βN₁/K₁)

in the absence of interspecific competition, β=0 and N₁=0 → the population of species 2 grows logistically to carrying capacity

what are the 2 possible outcomes of the interspecific competition equations?

1) drive species 1 to carrying capacity

2) drive species 2 to carrying capacity

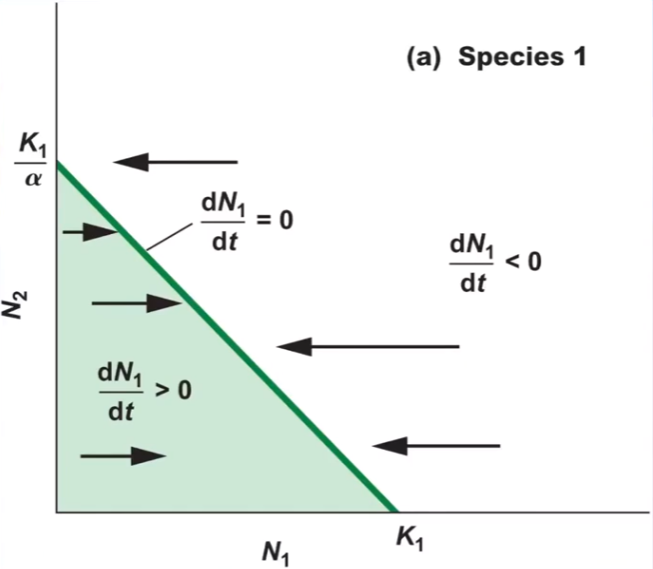
the effect of species # on # will drive species 1 to carrying capacity

2 on 1

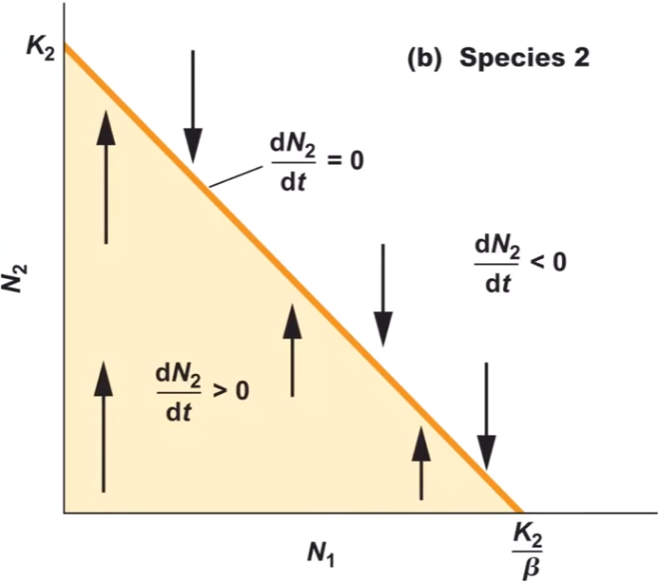
the effect of species # on # will drive species 2 to carrying capacity

1 on 2

what are the 4 possible outcomes of the lotka/volterra equations?

• one species is the superior competitor + wins out over the other

1) species 1 inhibits the population of 2 while continuing to increase

2) species 2 inhibits the population of 1 while continuing to increase

• each species, when abundant, inhibits the growth of the other (more than it inhibits its own growth)

3) eventually, one species wins

• each species inhibits its own population growth more than that of the other species

4) neither species eliminates the other → results in coexistence

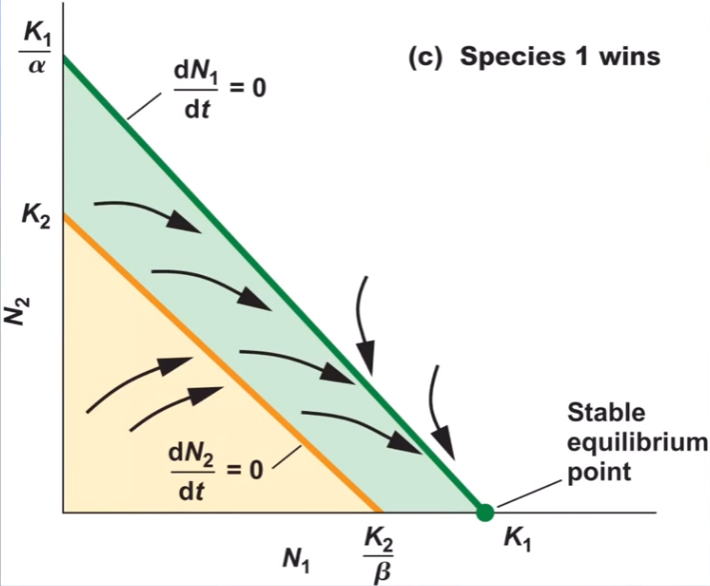
what is this graph showing you?

species 1 wins meaning that its carrying capacity is higher than species 2

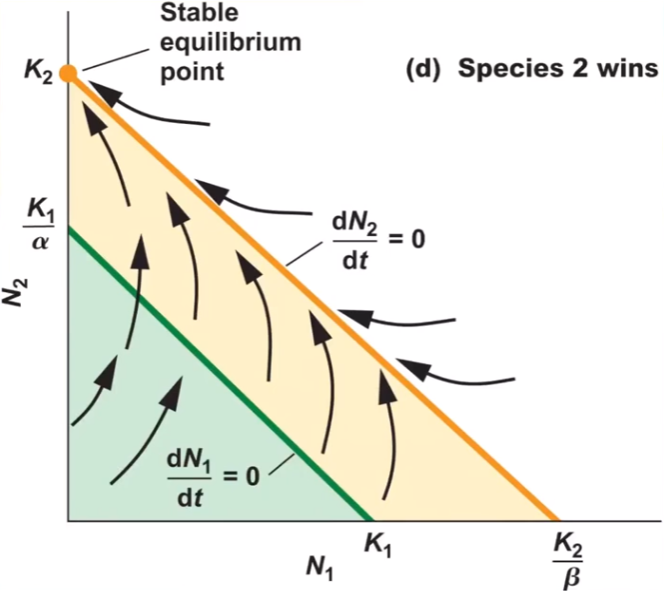
what is this graph showing you?

species 2 wins meaning that its carrying capacity is higher than species 1

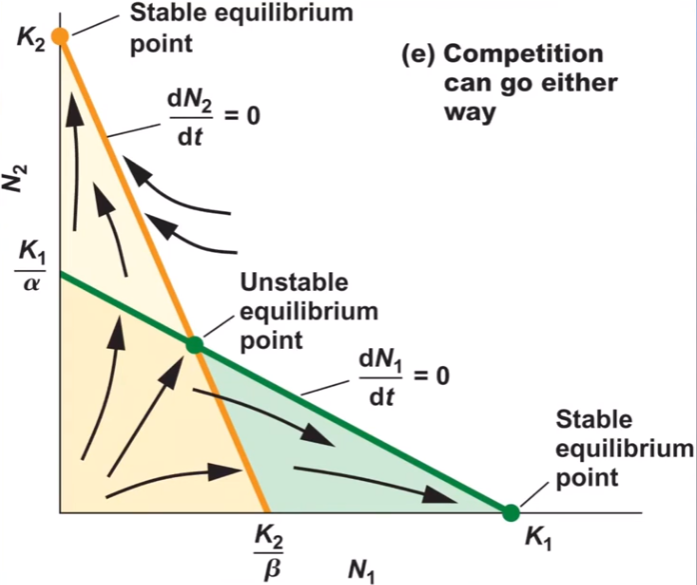
what is this graph showing you?

species 1 or 2 could win

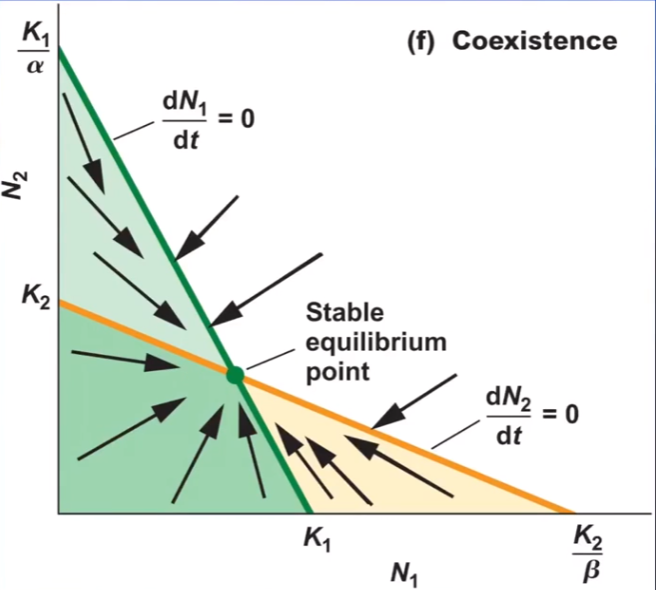
what is this graph showing you?

species 1 and species 2 don’t drive each other to carrying capacity → instead, they drive each other to coexistence