Module 2: 2-2: Displaying and Summarizing Data pt. 1

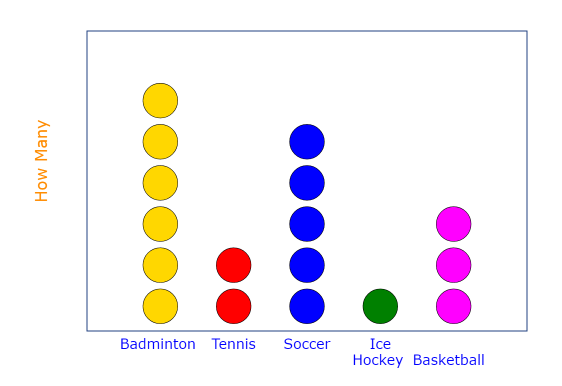
Dot plot

plot that portrays individual observations:

• number of dots above a value on the number line represents the frequency of occurence of that value

• work well for small sets of data

Shapes

nature of distribution:

• characterized by the number of humps or modes

• uniform, unimodal, bimodal, multimodal

Symmetry/Skewness

• part of the left is a mirror image of the part to the right

• Nonsymmetric graphs are skewed

• outlier: values that falls outside the overall pattern

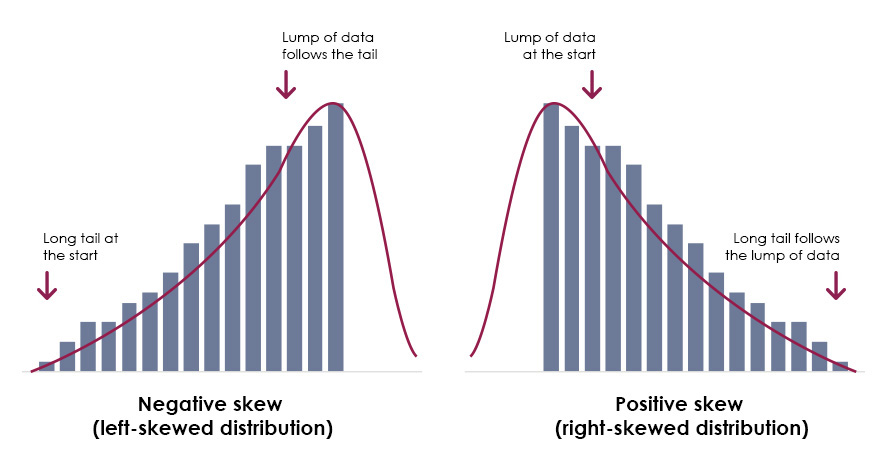
Skewed direction

+: large hump at left

-: large hump at right

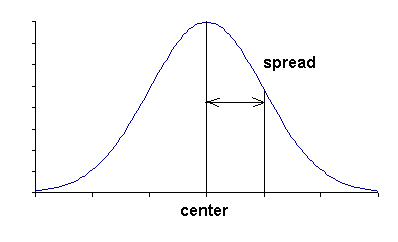
Center and Spread

• value that splits the data in half; mean, median, mode

• range of values; range, standard deviation, IQR

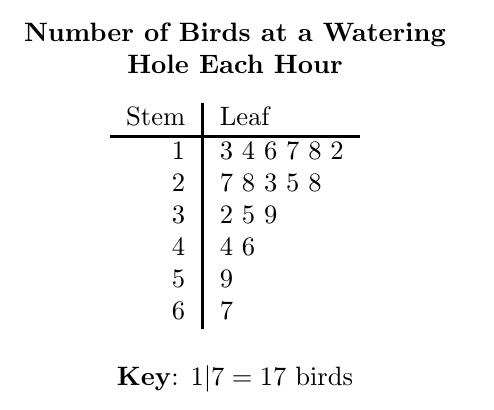
Stemplot

each number is broken into stems and leafs

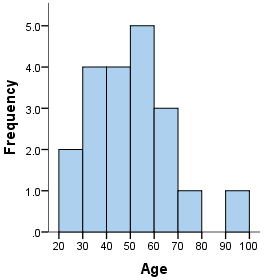
Histogram

visualizes the distribution of each variable well:

• no spaces

• quantitative

mean(u)

average number in a set of numerical observations

median(M)

value that divides sample set into two:

• if n is odd: single middle value

• if n is even: average(mean) of 2 middle values

mode

value with the highest frequency in the data set

Skewed distribution spreads:

+: mean > median > mode

-: mean < median < mode

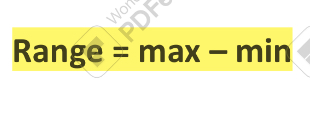
range

difference between the max and min of the value

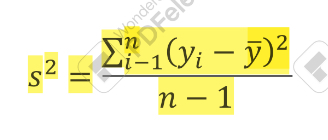
variance(s²)

sum of squared deviations from the mean divided by n-1

deviation

deviation of y from mean:

• +: y value is greater than mean

• -: value if smaller than mean

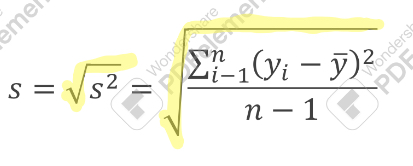
standard deviation

most common measure of variability, tells us how close the values of data set are clustered around the mean, square root of variance

standard deviation properties

• s = 0: no spread, observations are the same value

• s > 0: sd increases are observations become more spread out

• can only be used when mean is chosen as the measure of center