Functions

Independent Variable

Horizontal (x-value) - Can take any value

Dependent Variable

Vertical (y-value) - Depends on x value

Ways to represent independent/dependent

Mapping (choose an x, get the y)

Graphically

Function

Any independent value that produces one, and only one dependent value

Relation

Every graph, mapping, or equation is a relation. Independent values can produce one or more dependent values

Square Root Function vs. Square Root Operation

SR Function: y = \sqrt{x} (given, not produced, only positive)

SR Operation: y^2=x → y = \sqrt{x} (produced/inteoduced square root, +-, not function)

Vertical Line Test

Make an imaginary vertical line move across the cartesian plane. If it meets the curve more than once, it is not a function

Ordered Pair

Ex. {(3,6), (4,9), (5,2), (4,7), (2,6), (8,9)}

This set is a relation (x produce 1+ y)

Domain

The domain of a function or relation is the set of all independent values the function or relation can take

Number Systems (Continuous/Discrete)

Continuous: Real Numbers (Full line, every number touched) ~ Infinity numbers between every integer

Discrete: Integers (Dots, broken, only numbers listed are touched)

D: {x|xER}

R: {y|yER}

Domain is a set of x elements or real numbers such that x is an element of real numbers

Range is a set of y elements or real numbers such that y is an element of real numbers

* List values from least to greatest

End Point Possibilities

• - Is included

- - Is included

\omicron - Not included

Limit

When a line almost touches a point/number but doesn't (verryy close)

Range

The range of a function or relation is the set of all dependent values the function or relation can take

Represent Domain/Range Continuously/Discretely

Continuous: As a set

Discrete: As a list (Cuz its integers only)

f(x)

Function of X (not multiplication) = y

Parent Function

Non-transformed, non-translated functions

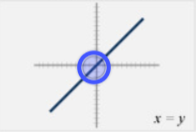
Parent Function - Linear

y = x

over 1, down 1 (As parent function)

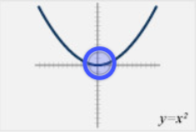
Parent Function - Quadratic

y = x^2

over 1, down 1 (As parent function)

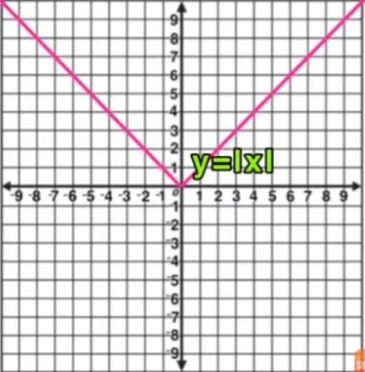
Parent Function - Absolute Value

y = |x|

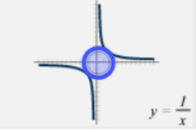
Parent Function - Inverse

y = 1/x

Piecewise Function

One function with multiple pieces to describe it

Asymptote

A line which a curve never touches (Gets super close or far)

Parent Function - Square Root

y = \sqrt{x}

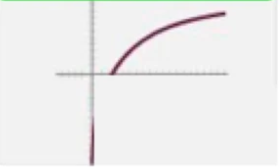
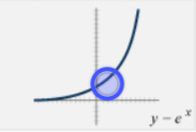
Parent Function - Exponential

y = b^{x}

b = base

asymptote at y = 0

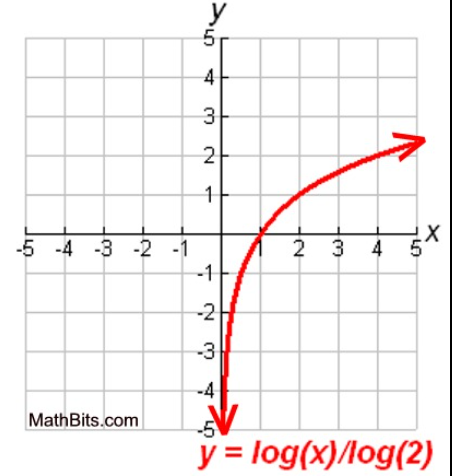
Parent Function - Logarithmic

y = \log b^{x}

* b is subscript

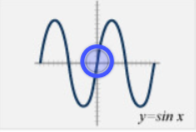
Parent Function - Sine

y = \sin x

Parent Function - Cosine

y = \cos x

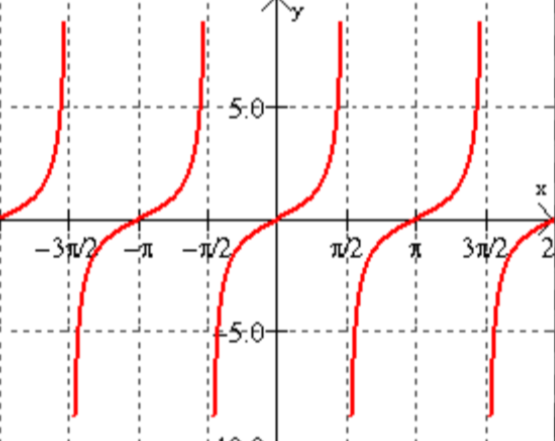
Parent Function - Tangent

\tan x=\sin x / \cos x

Sine/Cosine Rule

Always in between 1 and -1

How to find the Inverse of a Function?

Transpose the x and y values then resolve for y (Only one x and one y)

f^{-1} (x)

Transformations/Translations - a

a - vertical stretch/compress and inversion (Affect x-values)

If a > 1, it is a vertical stretch

If a is in between 0 and 1, it is a vertical compression

If a < 0, it is a vertical reflection (over x-axis)

* By a factor of

Transformations/Translations - c

c - Vertical Translation (Affect y-values)

If c > 0, it is vertically translated up by c

If c < 0, it is vertically translated down by c

Transformations/Translations - d

d - Horizontal Translation (Affect x-values)

If d > 0, it is a translation right by d

If d < 0 , it is a translation left by d

Transformations/Translations - k

k - Horizontal Stretch/Compression ~ cant do with simple curves (Affects x-values)

If k > 1, it is horizontally compressed by a factor of 1/k

If k is in between 0 and 1, it is a horizontal stretch by a factor of 1/k

If k < 0, it is a horizontal reflection (over y-axis)

* By a factor of

Will the inverse of a function always be a function?

For lines yes, anything with bumps (curve that changes direction) in it no.

Mapping Equations

y2 = a y1 + c

x2 = 1/k x1 + d