Chapter 4 StudyGuide

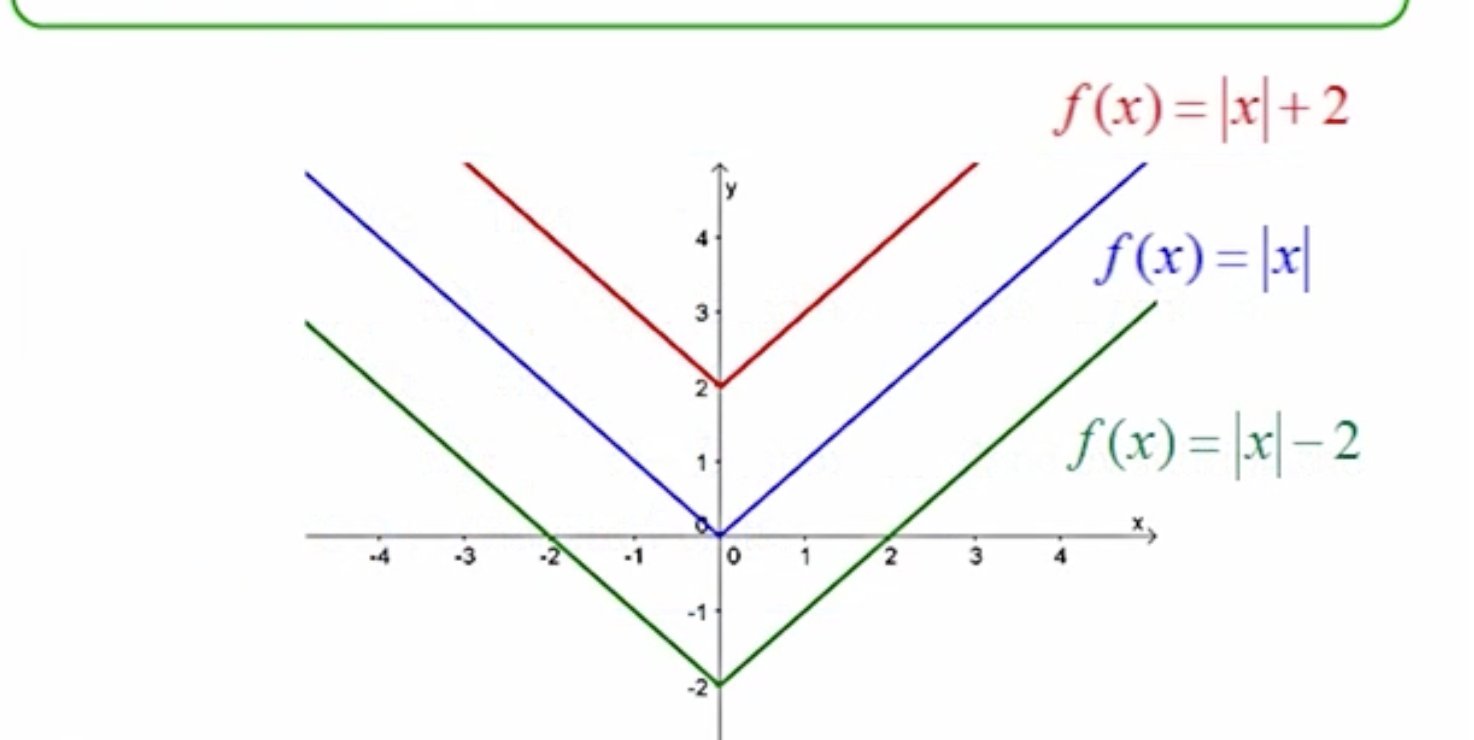
The graph: g(x)= f(x)+k, what does +k mean? (4.1)

The term +k represents a vertical shift upwards of the graph of f(x) by k units.

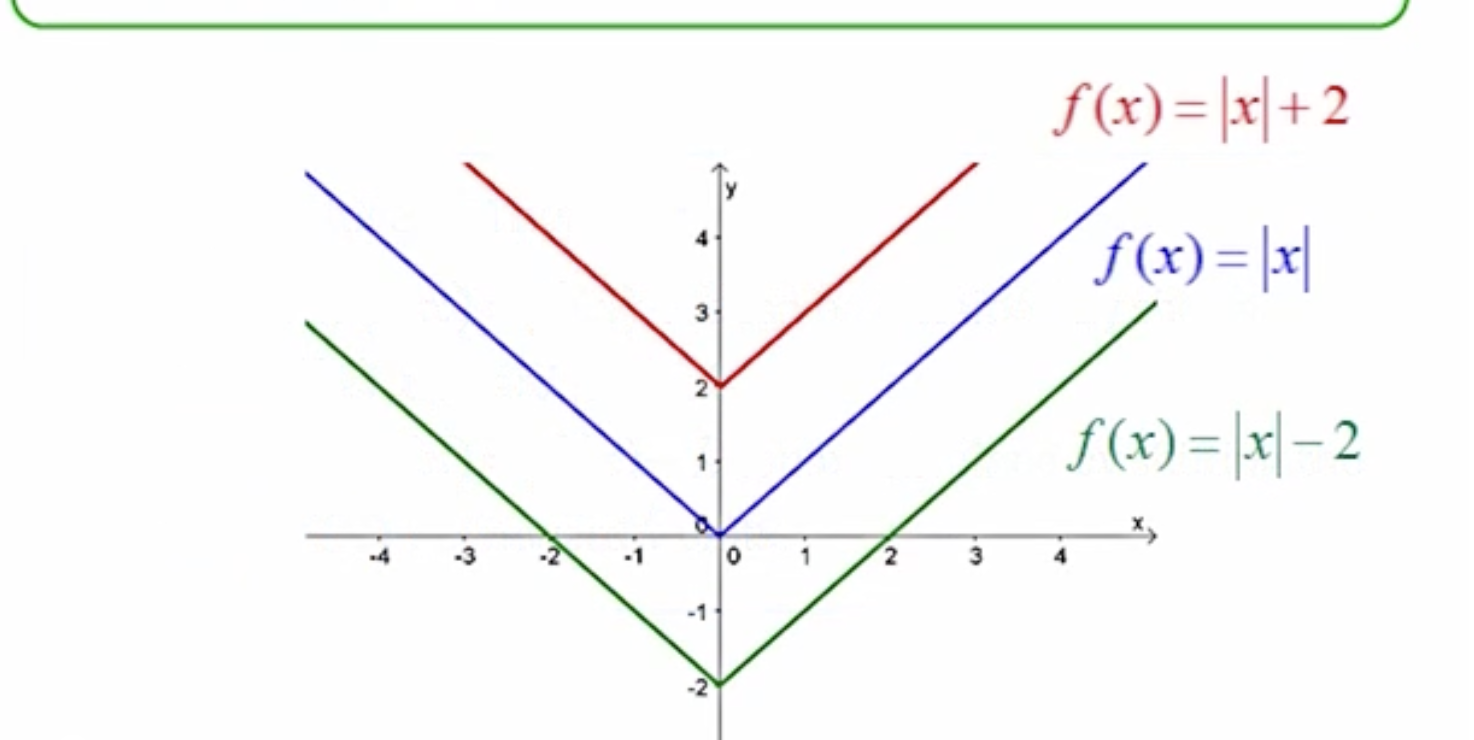
The graph: G(x)= f(x)-k, what does the -k mean (4.1)

The term -k represents a vertical shift downwards of the graph of f(x) by k units.

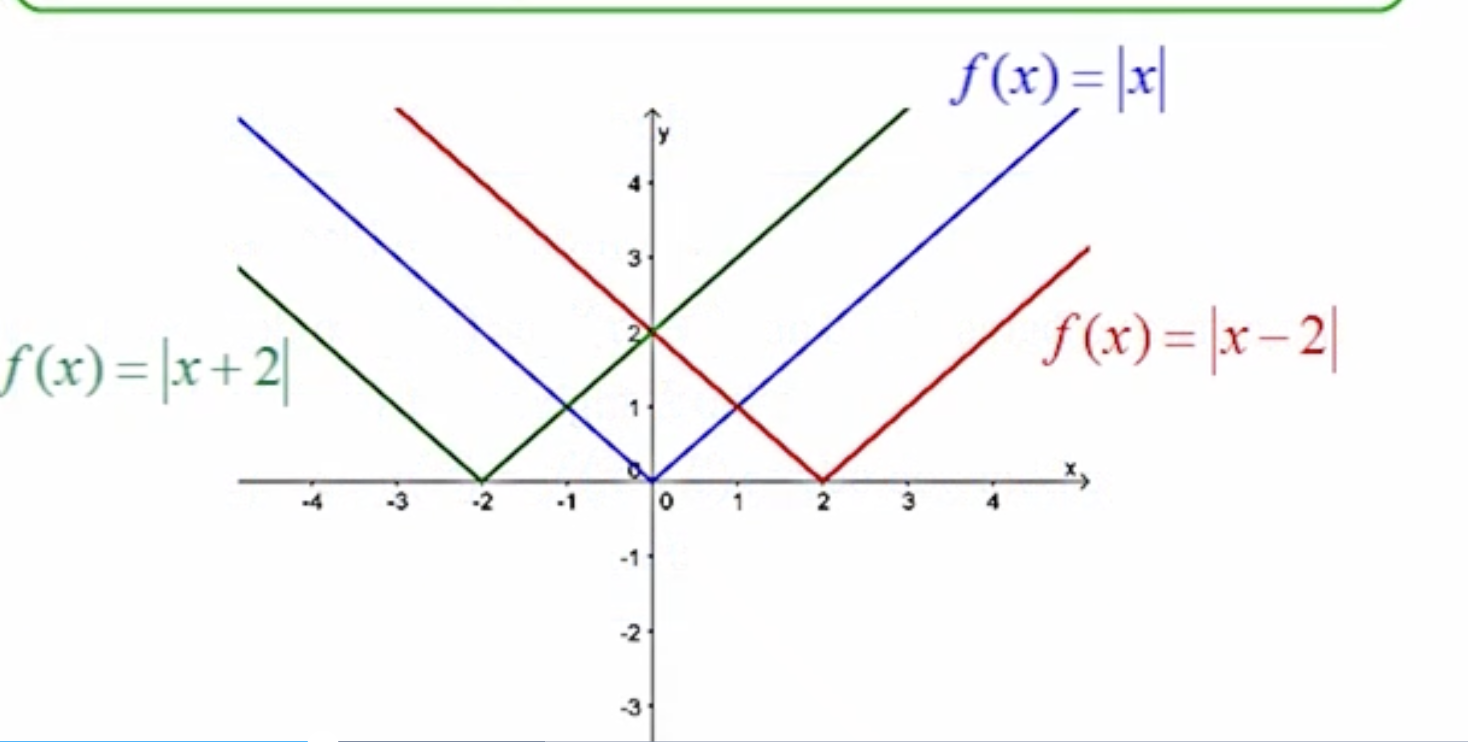
The graph: g(x)= f(x+k), what does the (x+k) mean? (4.1)

The term (x+k) represents a horizontal shift to the left of the graph of f(x) by k units.

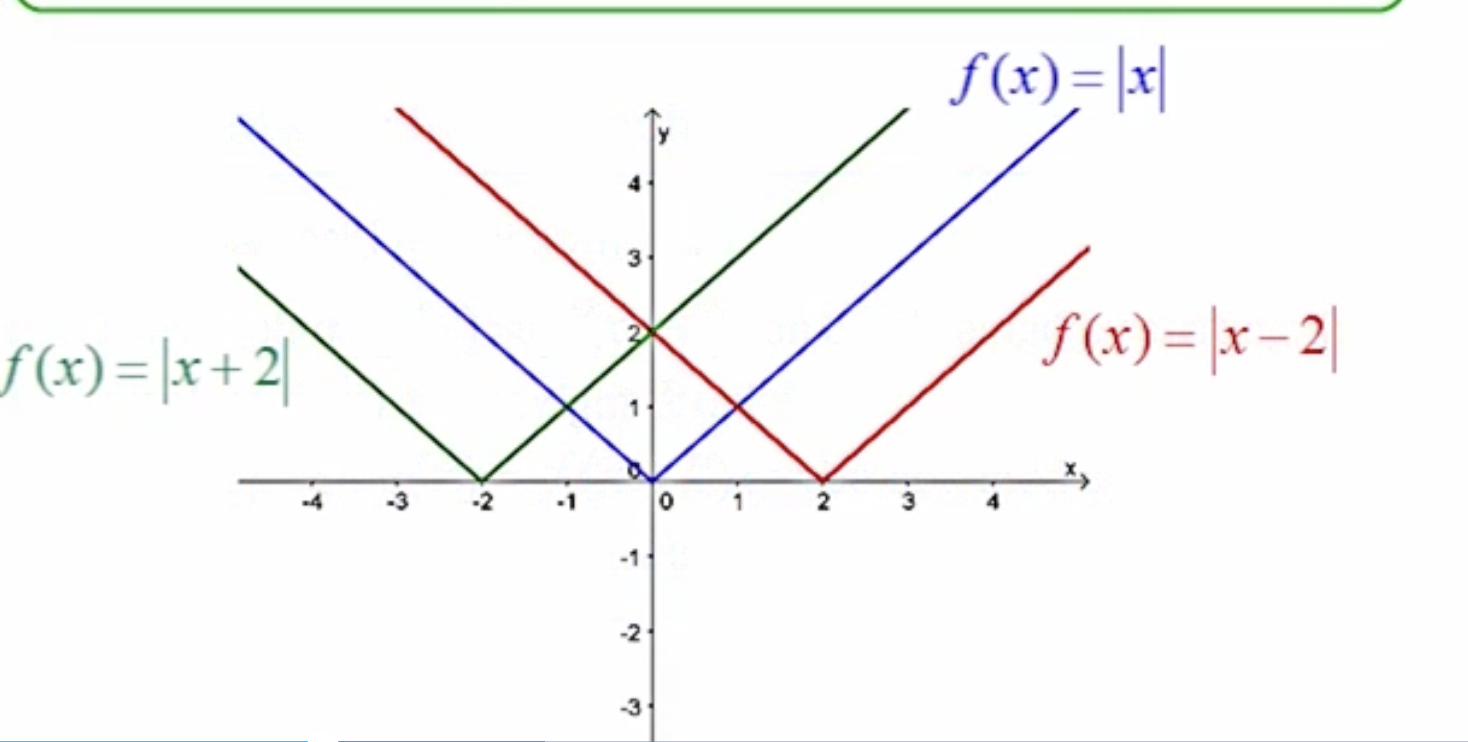
The graph: g(x)= f(x-k), what does the (x-k) mean? (4.1)

The term (x-k) represents a horizontal shift to the right of the graph of f(x) by k units.

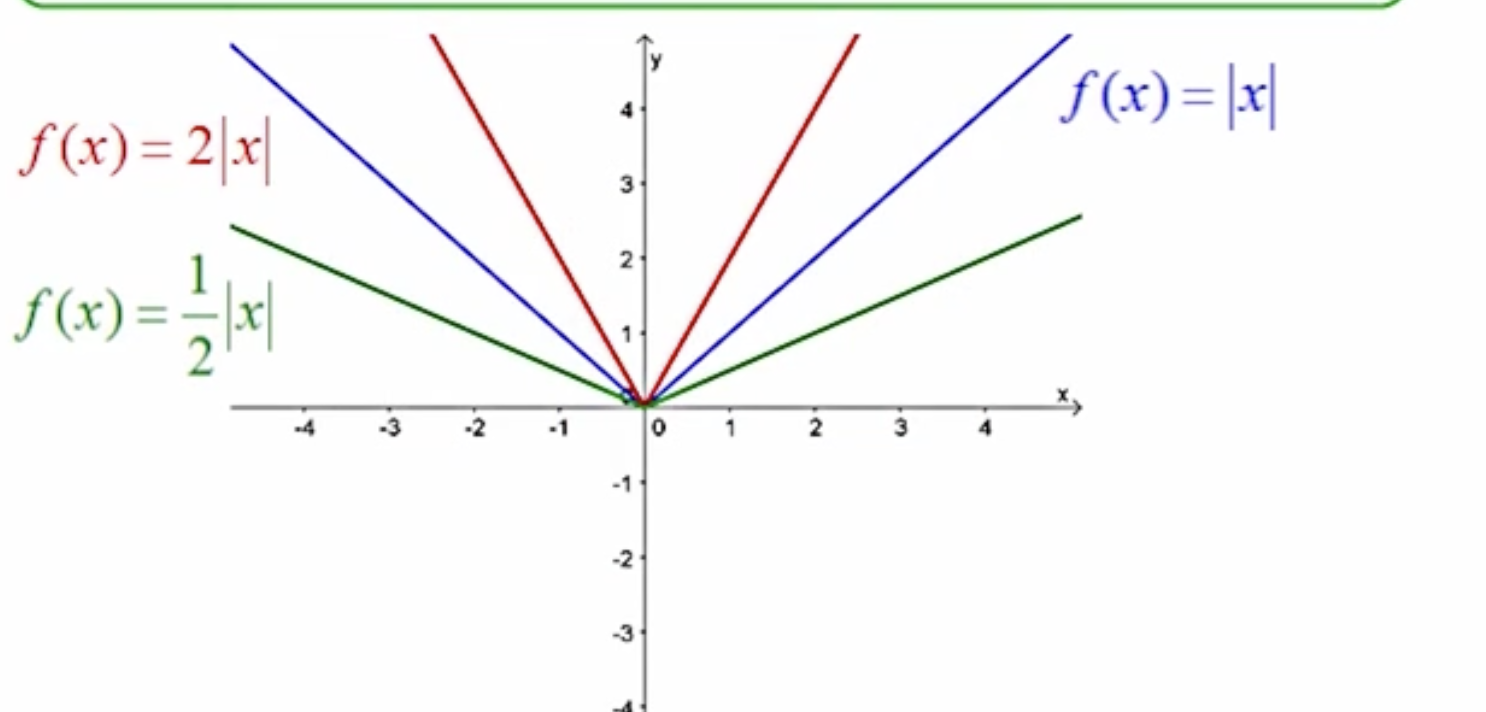
The graph: y=af(x), if |a| is greater than 1, what is happening? (4.1)

The term |a| greater than 1 indicates a vertical stretch of the graph of f(x) by a factor of a.

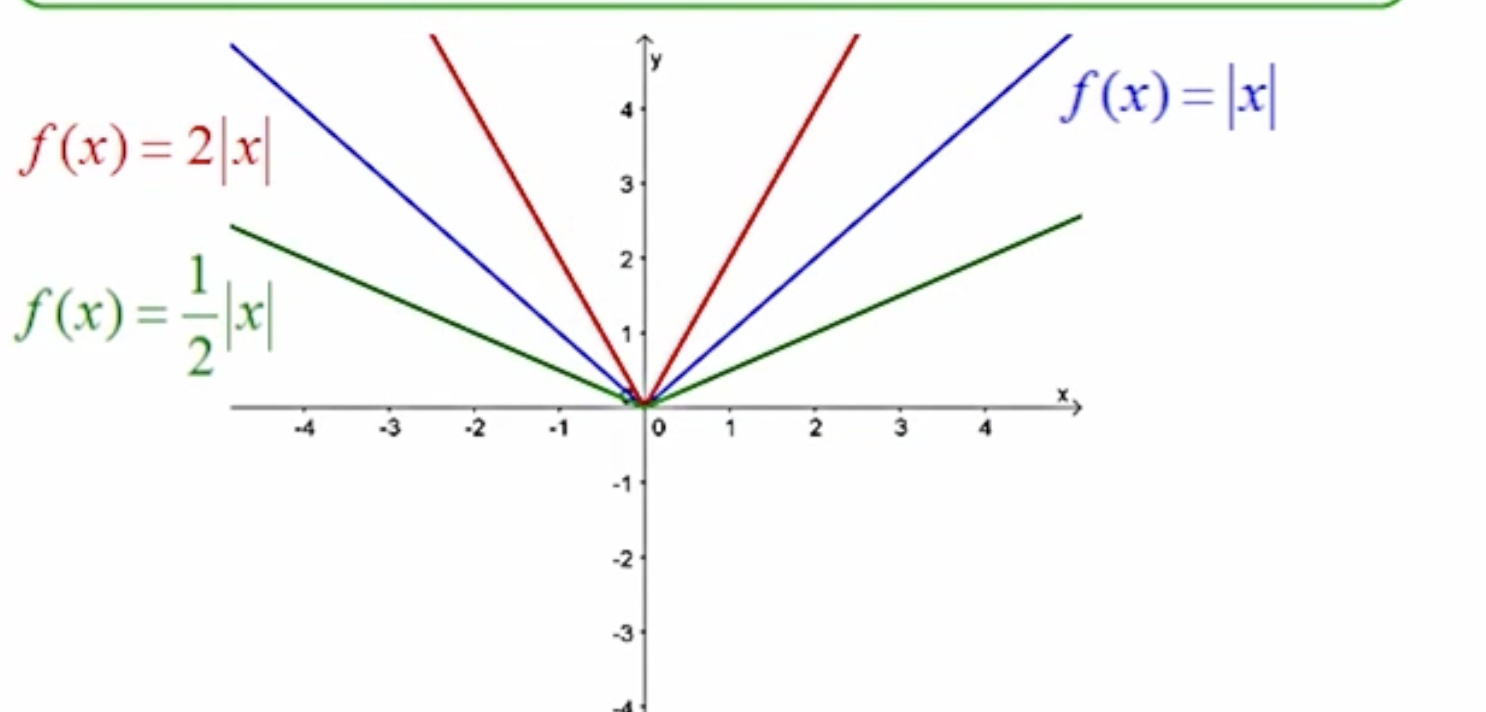
The graph: y=af(x), if |a| is greater than 0, but less than 1 (0<|a|<1) what is happening? (4.1)

The term |a| between 0 and 1 indicates a vertical compression of the graph of f(x) by a factor of a.

The graph: y=-f(x), what is happening? (4.1)

The term y=-f(x) indicates a reflection of the graph of f(x) across the x-axis.

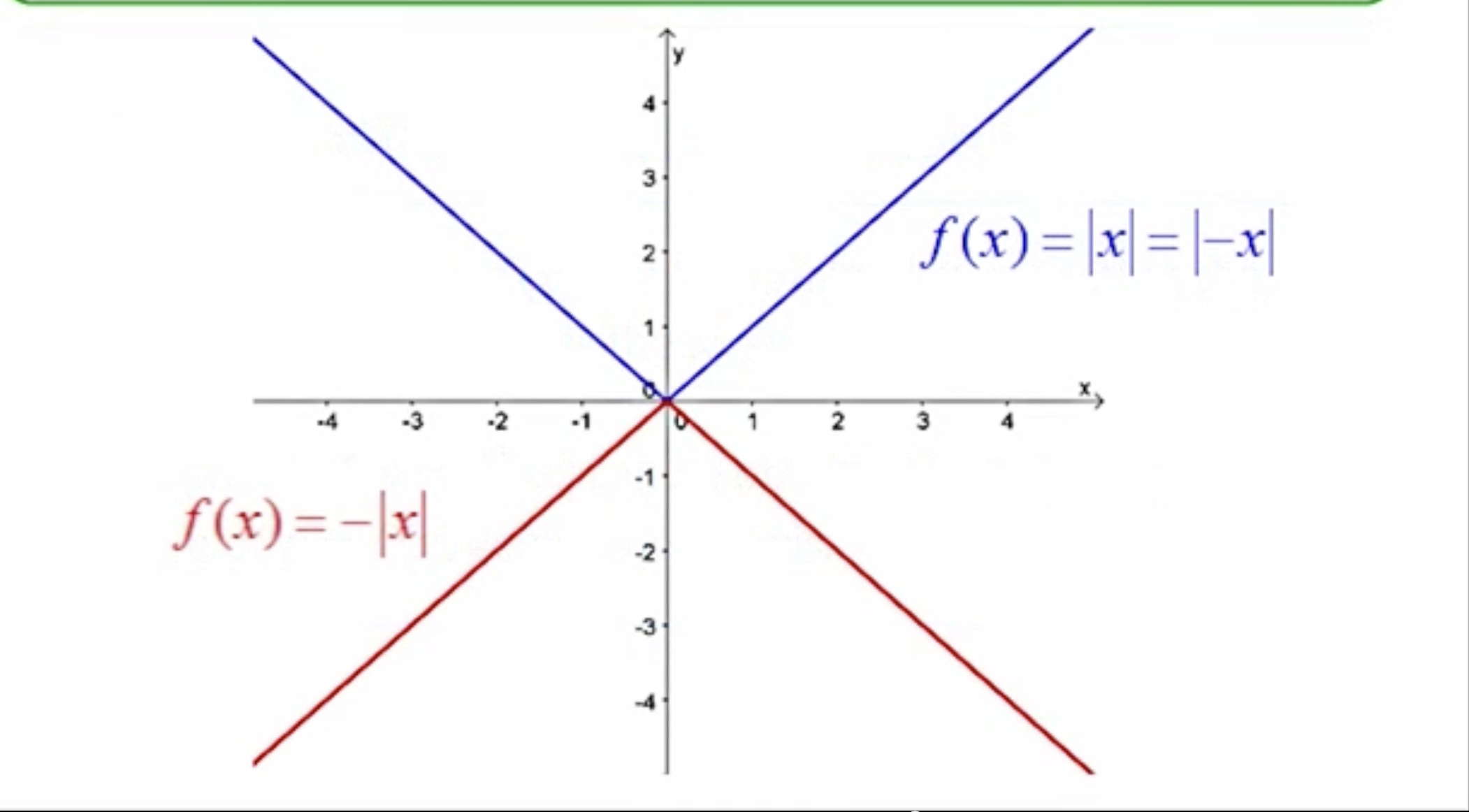
The graph: f(-x), what is happening? (4.1)

The term f(-x) indicates a reflection of the graph of f(x) across the y-axis.

A type of symmetry over an axis, for every (x,y) point on the graph, there is a (-x,y) point (4.1). Furthermore, what type of function is this?

This describes an even function, which is symmetric about the y-axis.

A type of symmetry over an axis, for every (x,y) point on the graph, there is a (x,-y) point (4.1)

This describes a function that is symmetric on the x-axis.

A type of symmetry on the graph. For every (x,y) point there is a (-x,-y) point. What type of function is this? (4.1)

This describes an odd function, which is symmetric about the origin.

A)Sketch

B) Compare first graph from 2nd. (4.1 )

• 1st) Graph both functions, y1= first equation, y2= second equation

• 2nd) Look at the graphs, and compare

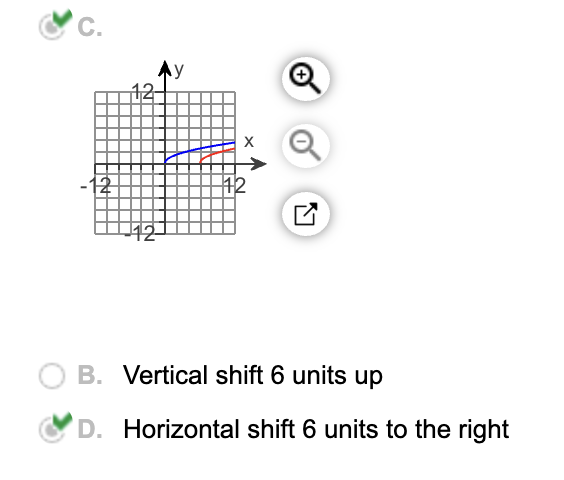
• Since (x-6) is inside the equation, the original graph shifted 6 units to the right.

Describe this function: From |x| → |x+8|-1 (4.1)

This function represents a transformation of the absolute value function. It is translated 8 units to the left and shifted down 1 unit.

Describe this function: From y=x² → y=-x²-5 (4.1)

This function represents a transformation of the quadratic function, reflecting it across the x-axis and translating it downward by 5 units.

Describe this function: from y=x² → y=(x+5)²-1 (4.1)

This function represents a transformation of the quadratic function, translating it 5 units to the left and shifting it down 1 unit.

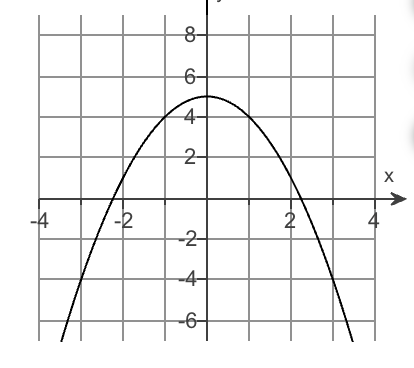
What happened from x²? (4.1)

It was a reflection across the x-axis and raised up by 5 units. meaning → -x²+5

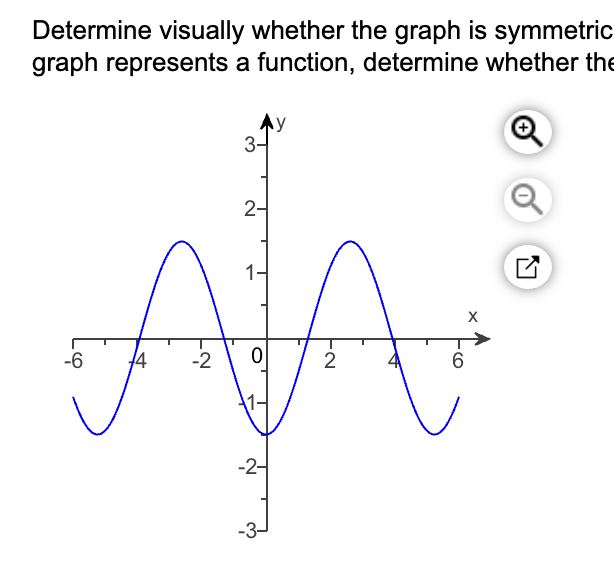
Describe the symmetry of this function (4.1)

The function is symmetric about the y-axis, meaning for every point (x, y) on the graph, the point (-x, y) is also on the graph, meaning it was an even function.

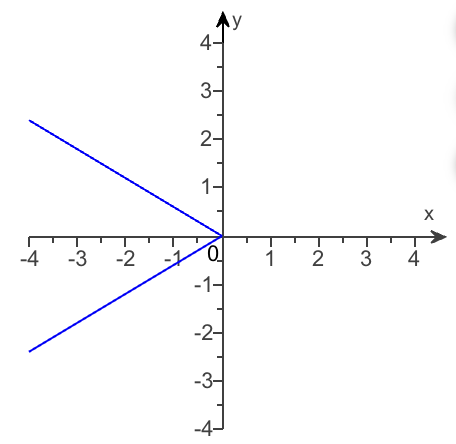
Describe the symmetry of this function (4.1)

This is symmetric for the x-axis. For every (x,y) point there is a (x,-y) point. It doesn’t represent an even or odd function.

How to graph this function and compare it?

• 4x²-7?

• First graph x²

• Graph 4x²-7

• Compare

How to find sums between two functions? (4.2)

f(x): x²-1, g(x)= 7+x

(f+g)(x)=f(x)+g(x)

• (x²-1)+(7+x)

• x²+1+7+x (Combine like terms)

• (f+g)(x) = x² + x + 6

How to find the difference between two functions? (4.2)

f(x): x²-1, g(x)= 7+x

(f-g)(x)=f(x)-g(x)

• (x²-1)-(7+x) “substitute the negative sign to the second function

• x²-1-7-x (Combine like terms)

• (f-g)(x) = x² - x - 8

How to find the product between two functions? (4.2)

f(x): x²-1, g(x)= 7+x

(f\cdot g)(x)=f(x)\cdot g(x)

• (x²-1)(7+x)

• 7x² + x³-7-x(Expand and combine)

• (f dot g)(x) =x³+7x²-x-7

How to find the Quotient between two functions (4.2)

f(x): x²-1, g(x)= 7+x

(f/g)(x)= f(x)/g(x)

• x²-1/7+x

This is the equation for average costs

C(x)= C(x)/x

How to compose two functions?

f(x): x²-1, g(x)= 7+x

f(g(x))= (7+x)²-1

g(f(x))=7+(x²-1)

To compose two functions, substitute one function into the other. For example, f(g(x)) means replacing g(x) in f(x).