Algo Eng - Class 9

Recursive Case

When function calls itself

Base Case

When function doesnt call itself again to prevent an infinite loop

Call Stack

Functions are put onto stack when called, includes recurrsions. Results in stack overflow error if stack is too big

Divide and Conquer

Strategy to divide problem into subproblems (problem is same as subproblem, repetitive structure), find solutions to said subproblems, then combine solutions to get solution to main problem

Decrease-by-one pattern

Each processing step reduces the number of input pieces by exactly 1, so a problem instance with n pieces requires n processing steps

Decrease-by-half pattern

Each processing step reduces the number of input pieces by roughly half, so only about log(n) processing steps are required

DCC Approach

Divide, Conquer, Combine

Recurrence Relation

T(…) for measuring with recurrences

Time Complexity (non-masters)

Ex: Test(n-1) → T(n-1), only take in account for then time complexities with the same block as the recursion call. Starting (top equation) is just 1 n = (whatever if statement condition is, ex: if(n>1) → 1 n = 1)

Minimum Selection Problem Recurrence Relation

2T(n/2) + O(1)

Summation Problem Recurrence Relation

2T(n/2) + O(1)

Master Theorem

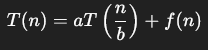
Master Theorem Case 1, If f(n) grows slower than n^(logb a)

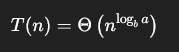
Master Theorem Case 2, If f(n) is equal to n^(logb a)

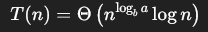
Master Theorem Case 3, If f(n) is bigger n^(logb a)

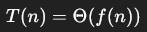
Master Theorem cannot be used if

1. T(n) is trigonometric

2. f(n) is not a polynomial

3. d cannot be expressed as a constant, ex T(n) = T(sqrt(n))

Maximum Sub Problem Recurrence Relation

T(n) = 2T(n/2) + n

Maximum Sub Problem Using Master’s Theorem

T(n) = O(n log n)

Merge Sort Recurrence Relation

T(n) = 2T(n/2) + n + 2

Merge Sort using Master’s Theorem

T(n) = O(n log n)

Merge Sort is a _____ algorithm

Stable Sorting

Stable Sorting Algorithm

When a sorting algorithm has the property that equal items appear in the final sorted list in the same relative order that they appeared in the initial input (i.e. ordering students in first attribute “name” then ordering students by second attribute “grade”, individuals with same grade, remain sorted by name)

Binary Search Recurrence Relation

T(n/2) + 5