Experimental Design Exam 1

Statistics

are two samples drawn from the same population.

gives info to help explain variation.

Biological differences

how large is the difference and is it important to biological function

Laplace and Gauss (1700s)

Created Normal Distribution and Central limit theorem

Normal Distribution

continuous probability distribution (bell curve)

Mean and median will be the same number

Central limit theorem

independent and identically distributed samples, the mean tends towards the normal distribution even if original variables are not normally distributed created by Laplace.

Galton and Pearson

Created correlation testing and chi-squared test. the second guy was the first to do formal statistical testing in the 1800s

Correlation

linear correlation between two sets of data, covariance of two variables and the product of their standard deviations (-1 to 1 perfect)

Chi-squared test

applied sets of categorical data to evaluate how likely that any observed difference between sets arose by chance (p value test)

Gosset and Fisher

T-test, ANOVA, Experimental design

T test started with the one who worked at a Guinness factory and published his work under the pseudonym “student”

was known as the “King of Genetics” he published 100s of articles on genetics.

Experimental Units (EU)

Able to retrieve treats i.e (A tank of water that has mercury added: the tank is the EU)

Some type of container (Box, tank, classroom, etc)

Measurement Unit (MU)

What is being measured. Units inside the container (Fish in a tank)

Problem with confusing MU for EU

Over optimistic analysis, rejection of H₀ , C.I. will be too short

Treatment Effect

What is being changed in an experiment

Degrees of freedom

maximum number of logically independent variables which may vary in a sample

Randomization

• A guard against situational errors

• requires identification of all the objects that might be selected

• Used in selection in the field and setting up the experiment

• Can be used when their is a limited sample

Skew

direction a normal distribution (bell curve) graph leans

Left skew

√b1 < 0

No skew

√b1 = 0

Right skew

√b1 > 0

Kurtosis

The peakedness of the normal distribution graph (bell curve)

Broad v Narrow

Platykurtic - broad

b₂ < 3

mesokurtic

b₂ = 3

leptokurtic

b₂ > 3

Random Selection with Replacement

The Best form of Randomization

1. tag entire population of interest, so every individual has a unique identifying number

2. random selection of individuals (cards, dice, random number table)

3. measure the selected individual

4. replace the individual back in the population before makin the next selection

5. the probability of selection remains constant

Fisher has said

“Random assignment of treatments is required”

In a t-test; as N increases

t decreases, and SE (standard error) decreases

Replication

Most important part of experimental design

Most messed up

Experimental Design

Randomization + Replication

1. Plan Experiment ← Chose stats analysis then

2. Carry out experiment - data collection (where experimenters typically go wrong)

3. Run stats on data

Factor

Treatment - Independent variable - x-axis

Variable

Measured - dependent variable - y-axis

Variation

is everywhere in the real world.

Includes Measurement error (ME), Natural inherent variation, variation in individuals, variation in mean values

Means by themselves explains nothing.

ME

due to limitations of people, instruments, and environment

Natural Inherent variation

Genetics, biological processes, environmental history

Variation in individuals

Sample standard deviation

Variation in mean values

Sample of means standard deviation, standard error of the mean (SEM)

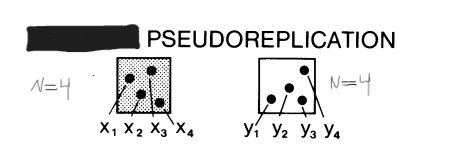
Simple Pseudoreplication

There are single replicates of EU per treatment with nested MU

Shouldn’t run stats - Observation tests only (due to lack of significant difference)

Happens with large scale experiments

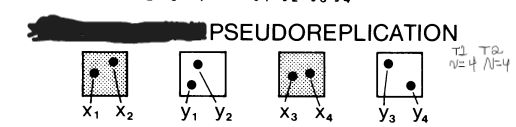
Sacrificial Pseudoreplication

true replication of treatments but data for replicates are pooled for statistical analysis (sacrifices independence by using individuals as EU not MU) confuses MU for EU which gives a larger n value leading to a wrong df → wrong df error term → wrong MS Error term  → wrong F term → incorrect P value which would create an incorrect interpretation and assumptions.

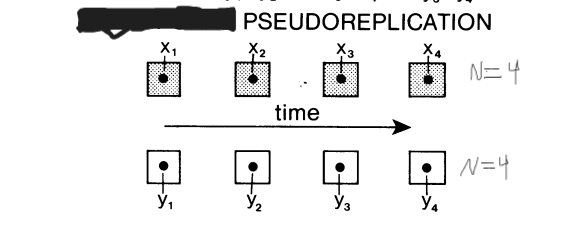
Temporal Pseudoreplication

multiple samples from each EU (one per treatment) are not taken simultaneously but instead over several dates

Treats each measurement as a separate EU.

Don’t treat successive dates as independent replicates of a treatment

• no longer independent - same sample multiple times

• need multiple EU over time

Implicit Pseudoreplication

When Standard Error and Confidence Interval is reported along with their means and discuss the effects of the treatments, but there is no application of any direct tests of significance. It is psuedoreplication when if the experimenter does not give a specific disclaimer acknowledging that their data is inadequate for assessing treatment effects. 

If only standard deviation is presented than it isn’t psuedoreplication.

SE of a sample

is an estimate of the variation of means

Difference between Treatment

EU - variation regardless of treatments

MU - variation among MU regardless of treatment

TE - variation caused by treatment effect

Difference withing treatment

EU - variation among EU

MU - variation among MU

Independent Error Terms

Is all based on design

HOV (draw table)

Variances of treatments are similar for test of means to be accurate

MS (mean square) - variance within treatments

• one number to tell if treatments are different

Uses pooled variance in calculation

is an assumption because all variances have to all be the same for it to be accurate if one number is off  the resulting calculations could all be off i.e. if the F-value is off the P-value is off.

ANOVA table

Top row - between treatments

Bottom row - within treatments (error)

Represents the variation of means among treatments.

Change in the variance is an indication in the change the biologist made

Change in the mean might not happen

Variance carries biological information from the outcome.

F

between treatments/within = TE + all other variation/all other variation = treatment effect + EU + MU / EU + MU

• Everything cancels out to just leave TE

  • If others don’t cancel, wrong analysis of treatment effect and generates wrong F term (typically caused by improper replication)

P values

Value less than alpha reject H₀ if larger don’t reject H₀

Represents the probability of getting a more extreme result than what the data set says.

Area under the curve outside of the data set.

Used when you design an experiment on purpose the value can be used for interpretation.

Change when there is a change in sample size

Type 1 error

alpha: reject H₀  is wrong (usually happens if p value is very large

to lower in crease n

Type 2 error

Beta - fail to reject H₀ is wrong

Random Selection without Replacement

1. tag entire population of interest, so every individual has a unique identifying number

2. random selection of individuals (cards, dice, random number table)

3. measure the selected individual

4. do not replace the individual back in the population before making the next selection

5. the probability of selection changes, but in a predictable way

Haphazard Selection

1. do not tag entire population, or any of the population of interest

2. no random selection, pick up whatever you find, or buy things from supply houses

3. measure individual

4. replacement is irrelevant, but usually does not happen

5. there is no probability of selection

J

bias correction factor

used to adjust for sample size

One-Sample t-Test

Tests a single factor at only one treatment level/sample against a null test mean μ: mean of Column A1 = null test mean μ

Ex: A factory is measuring if the average box of cereal contains 24oz cereal compared to the hypothesized value of 24 oz.

√s2/ n

level of variation

Effect size

The replacement for p for non-strict science journals

Larger number more effect there is

opposite direction of p-value

< 0.2 : small, around 0.5 in the middle, > 0.8 : large, and >2.0 : very large

Does not change with sample size

S²

Variation within

Further variance gets less accurate

One-factor Completely Randomized ANOVA

One Factor of multiple treatment levels

How you randomize defines the design

How design defines how you analyze

Step 1: Randomly assign treatments to EU matching one list of treatment numbers with one list of EU numbers in random order → design

Step 2: Randomly assign MUs to EUs matching one list of MU numbers with one list of EU numbers in random order → helps remove bias

H₀: mean of each column is the same as the other.

One-factor Completely Randomized ANOVA Assumptions

Assumptions: The data points withing each column (treatment group) are from randomly drawn individuals, and are normally distributed

The data points are independent of one another within and between columns (treatment groups) (the within relates to independent replication of EU within each treatment; the between relates to the completely randomized design across all treatments).

The variances of the columns (treatment groups) are similar

One-Sample t-test Assumption

Assumptions: The data points are from randomly drawn individuals, normally distributed, and independent of one another

SS

sum of squares of a column

start of calculations for variation

ω² (omega)

the effect size given is a biased-corrected estimate of effect size compared to η²

η² (eta)

effect size estimate for effect or factor of interest

gives the percent amount of how much a Factor is apart of the variation in SS in the ANOVA

The more of the variation in the ANOVA table that a factor explains the more important

Two-Sample (Independent) t-Test

Used when there is only two treatment groups for one factor

The design and set up is identical to the One-Factor Completely Randomized ANOVA.

Effect size is calculated differently.

H₀: mean of Column A1 = mean of Column A2

Welch t-test

Used when there are only two treatment groups for one factor.

t-value uses separate variance instead of the pooled variance.

H₀: mean of Column A1 = mean of Column A2

Welch t-test assumption

Same as One-Factor Completely Randomized ANOVA except homogeneity of variance is not required.

Two-Sample (Independent) t-Test

Same as One-Factor Completely Randomized ANOVA

Cohen’s d^*_s

effect size estimate based on the average variance

Hedges g^*

Cohen’s d^*_s bias correction factor

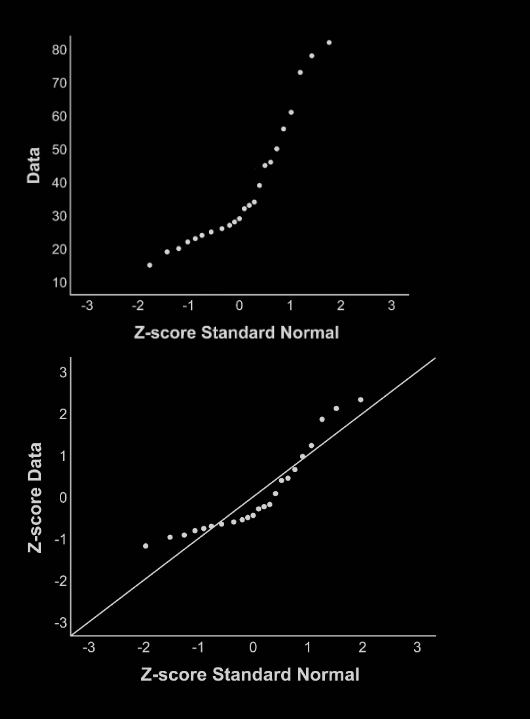
Normal probability plots

If all dots line up in a straight line you have normal data