Honors Geometry - Special Segments in Triangles and Points of Concurrency

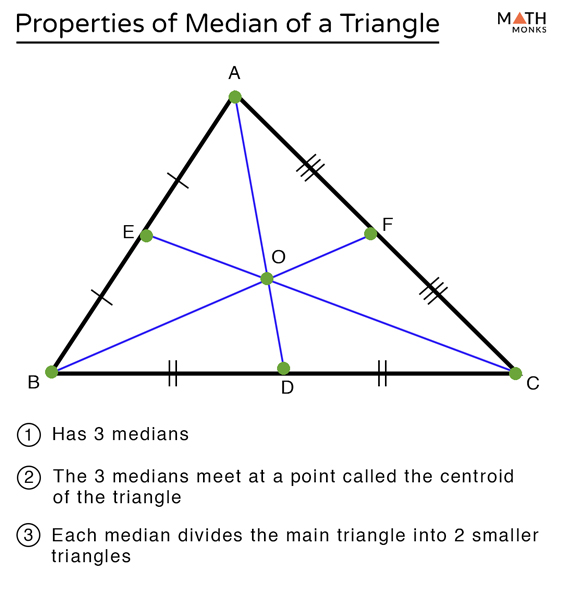
Median

A segment from a vertex to the midpoint of the opposite side

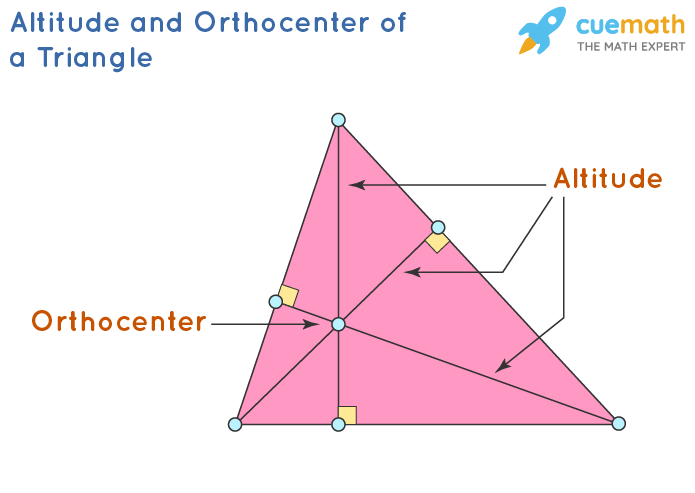
Altitude

The perpendicular segment from a vertex to the line that contains the opposite side

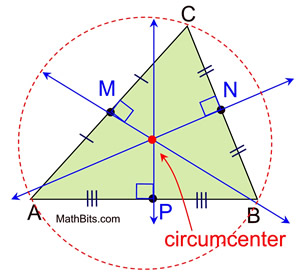
Perpendicular Bisector

A line, ray, or segment that is perpendicular to the segment at its midpoint

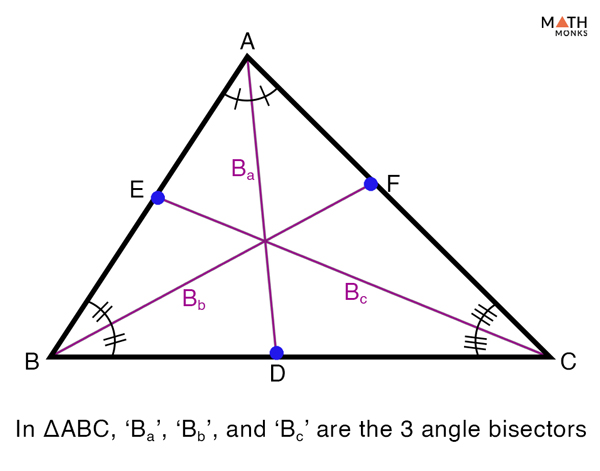
Angle Bisector

A line or ray that divides an angle into two congruent angles

Point of Concurrency

Point of intersection for 3+ lines

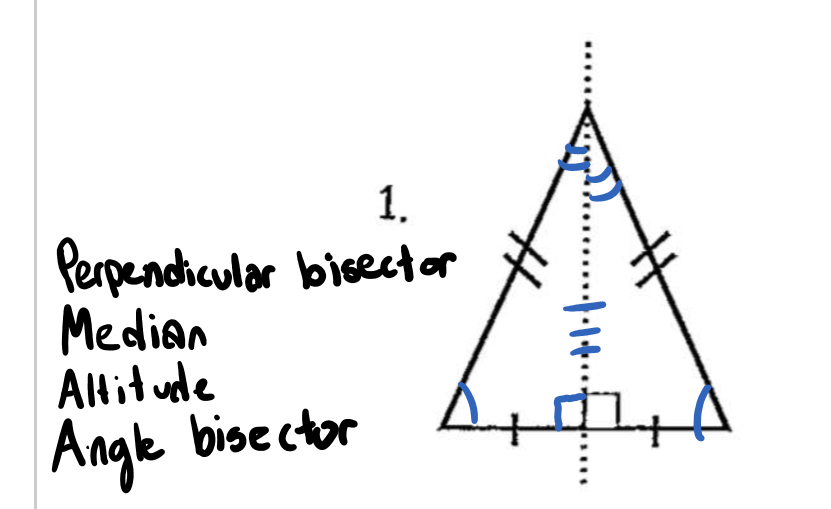
Example of a triangle with all four special segments

Acronym to remember points of concurrency

All of - Altitude/orthocenter

my children - Median/centroid

are bringing in - Angle bisector/incenter

PB cookies - Perpendicular bisector/circumcenter

Point of concurrency for angle bisectors

Incenter

Point of concurrency for medians

Centroid

Point of concurrency for a perpendicular bisectors

Circumcenter

Point of concurrency for altitudes

Orthocenter

How to find the equation for an altitude

1. Find the ordered pair for vertex (where the altitude is coming from)

2. Find the opposite reciprocal slope of the line opposite to the vertex

3. Use point slope form to find the equation. Use the ordered pair (vertex) from step 1 and the slope from step 2

How to find the orthocenter

1. Find the equation for 2 of the 3 altitudes of the triangle

2. Put the point slope form into slope intercept form

3. Set the equations equal to find the ordered pair, which is the orthocenter

How to find the equation for a median

1. Find the ordered pair for the vertex (where the median is coming from)

2. Find the midpoint of the line opposite the vertex using the midpoint formula

3. Find the slope from the vertex to the midpoint

4. Use point slope form to find the equation. Use the ordered pair (vertex) from step 1 and the slope from step 3

How to find the centroid

1. Find the equation for 2 of the 3 medians of the triangle

2. Set both equations from point slope form to slope intercept form

3. Set the equations equal to find an ordered pair, which is the centroid

How to find the equation of a perpendicular bisector

1. Find the midpoint of the line the perpendicular bisector bisects using the midpoint formula

2. Find the opposite reciprocal slope of the line the perpendicular bisector bisects

3. Use point slope form to find equation. Use ordered pair from step 1 and the slope from step 2.

How to find the circumcenter

1. Find the midpoint of the three lines

2. Find the opposite reciprocal slope using the two endpoints on the line

3. Use point slope form to find the equation of the circumcenter. Use the midpoint from step 1 and the slope from step 2.

4. Repeat steps 1, 2, and 3 for another line

5. Put both of these lines into slope intercept form and set them equal to find the circumcenter